Location: hypar/Examples/1D/LinearAdvection/SineWave (This directory contains all the input files needed to run this case. If there is a Run.m, run it in MATLAB to quickly set up, run, and visualize the example).
Governing equations: 1D Linear Advection Equation (linearadr.h)
References:
- Ghosh, D., Baeder, J. D., "Compact Reconstruction Schemes with
Weighted ENO Limiting for Hyperbolic Conservation Laws", SIAM Journal on Scientific Computing, 34 (3), 2012, A1678–A1706
Domain: \(0 \le x < 1\), "periodic" (_PERIODIC_) boundary conditions
Initial solution: \(u\left(x,0\right) = \sin\left(2\pi x\right)\)
Numerical Method:
Input files required:
solver.inp
begin
ndims 1
nvars 1
size 80
iproc 1
ghost 3
n_iter 400
time_scheme rk
time_scheme_type ssprk3
hyp_space_scheme crweno5
conservation_check yes
dt 0.0025
screen_op_iter 10
file_op_iter 40
ip_file_type ascii
op_file_format text
op_overwrite no
model linear-advection-diffusion-reaction
end
boundary.inp
2
periodic 0 1 0 0
periodic 0 -1 0 0
physics.inp
lusolver.inp (optional)
begin
reducedsolvetype jacobi
evaluate_norm 1
maxiter 10
atol 1e-12
rtol 1e-10
verbose 0
end
weno.inp (optional)
begin
mapped 1
borges 0
yc 0
no_limiting 0
epsilon 0.000001
p 2.0
rc 0.3
xi 0.001
end
To generate initial.inp, compile and run the following code in the run directory. Note: if the final time is an integer multiple of the time period, the file initial.inp can also be used as the exact solution exact.inp (i.e. create a sym link called exact.inp pointing to initial.inp, or just copy initial.inp to exact.inp).
#include <stdio.h>
#include <stdlib.h>
#include <math.h>
#include <string.h>
double pi = 4.0*atan(1.0);
int NI,ndims;
char ip_file_type[50];
strcpy(ip_file_type,"ascii");
FILE *in;
printf("Reading file \"solver.inp\"...\n");
in = fopen("solver.inp","r");
if (!in) printf("Error: Input file \"solver.inp\" not found. Default values will be used.\n");
else {
char word[500];
fscanf(in,"%s",word);
if (!strcmp(word, "begin")){
while (strcmp(word, "end")){
fscanf(in,"%s",word);
if (!strcmp(word, "ndims")) fscanf(in,"%d",&ndims);
else if (!strcmp(word, "size")) fscanf(in,"%d",&NI);
else if (!strcmp(word, "ip_file_type")) fscanf(in,"%s",ip_file_type);
}
} else printf("Error: Illegal format in solver.inp. Crash and burn!\n");
}
fclose(in);
if (ndims != 1) {
printf("ndims is not 1 in solver.inp. this code is to generate 1D initial conditions\n");
return(0);
}
printf("Grid:\t\t\t%d\n",NI);
int i;
double dx = 1.0 / ((double)NI);
double *x, *u;
x = (double*) calloc (NI, sizeof(double));
u = (double*) calloc (NI, sizeof(double));
for (i = 0; i < NI; i++){
x[i] = i*dx;
u[i] = sin(2*pi*x[i]);
}
FILE *out;
if (!strcmp(ip_file_type,"ascii")) {
printf("Writing ASCII initial solution file initial.inp\n");
out = fopen("initial.inp","w");
for (i = 0; i < NI; i++) fprintf(out,"%lf ",x[i]);
fprintf(out,"\n");
for (i = 0; i < NI; i++) fprintf(out,"%lf ",u[i]);
fprintf(out,"\n");
fclose(out);
} else if ((!strcmp(ip_file_type,"binary")) || (!strcmp(ip_file_type,"bin"))) {
printf("Writing binary initial solution file initial.inp\n");
out = fopen("initial.inp","wb");
fwrite(x,sizeof(double),NI,out);
fwrite(u,sizeof(double),NI,out);
fclose(out);
}
free(x);
free(u);
return(0);
}
Output:
After running the code, there should be 11 output files op_00000.dat, op_00001.dat, ... op_00010.dat; the first one is the solution at \(t=0\) and the final one is the solution at \(t=1\). Since HyPar::op_overwrite is set to no in solver.inp, separate files are written for solutions at each output time. All the files are ASCII text (HyPar::op_file_format is set to text in solver.inp). In these files, the first column is grid index, the second column is x-coordinate, and the third column is the solution.
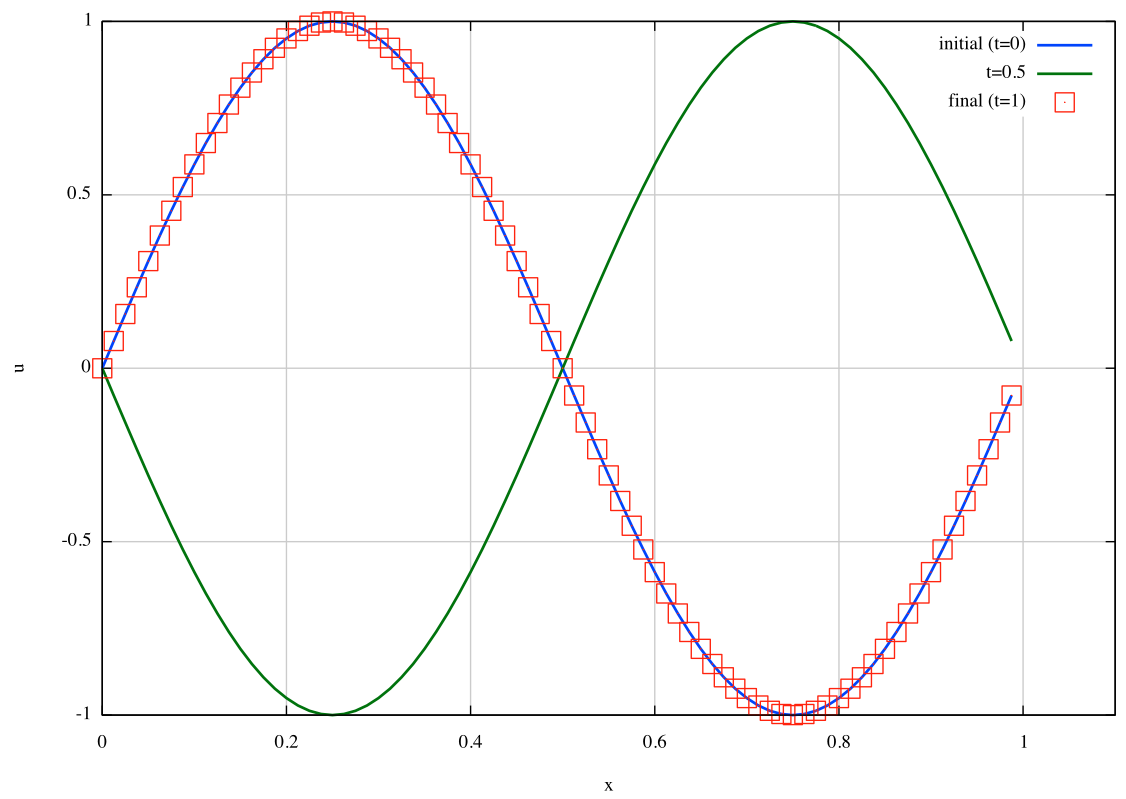
Solutions at t=0,0.5,1: The following figure is obtained by plotting op_00000.dat (initial), op_00005.dat (t=0.5), and op_00010.dat (final).
Since the exact solution is available at the final time (exact.inp is a copy of initial.inp), the numerical errors are calculated and reported on screen (see below) as well as errors.dat:
80 1 2.5000000000000001E-03 1.0521708205329536E-06 1.0871437024745659E-06 1.3438402750587386E-06 9.4072000000000003E-02 9.4830999999999999E-02
The numbers are: number of grid points (HyPar::dim_global), number of processors (MPIVariables::iproc), time step size (HyPar::dt), L1, L2, and L-infinity errors (HyPar::error), solver wall time (seconds) (i.e., not accounting for initialization, and cleaning up), and total wall time.
Since HyPar::ConservationCheck is set to yes in solver.inp, the code checks for conservation error and prints it to screen, as well as the file conservation.dat:
80 1 2.5000000000000001E-03 2.2117724318704290E-17
The numbers are: number of grid points (HyPar::dim_global), number of processors (MPIVariables::iproc), time step size (HyPar::dt), and conservation error (HyPar::ConservationError).
Expected screen output:
HyPar - Parallel (MPI) version with 1 processes
Compiled with PETSc time integration.
Reading solver inputs from file "solver.inp".
No. of dimensions : 1
No. of variables : 1
Domain size : 80
Processes along each dimension : 1
No. of ghosts pts : 3
No. of iter. : 400
Restart iteration : 0
Time integration scheme : rk (ssprk3)
Spatial discretization scheme (hyperbolic) : crweno5
Split hyperbolic flux term? : no
Interpolation type for hyperbolic term : characteristic
Spatial discretization type (parabolic ) : nonconservative-1stage
Spatial discretization scheme (parabolic ) : 2
Time Step : 2.500000E-03
Check for conservation : yes
Screen output iterations : 10
File output iterations : 40
Initial solution file type : ascii
Initial solution read mode : serial
Solution file write mode : serial
Solution file format : text
Overwrite solution file : no
Physical model : linear-advection-diffusion-reaction
Partitioning domain.
Allocating data arrays.
Reading array from ASCII file initial.inp (Serial mode).
Volume integral of the initial solution:
0: 4.9005938196344800E-17
Reading boundary conditions from "boundary.inp".
Boundary periodic: Along dimension 0 and face +1
Boundary periodic: Along dimension 0 and face -1
2 boundary condition(s) read.
Initializing solvers.
Reading WENO parameters from weno.inp.
Initializing physics. Model = "linear-advection-diffusion-reaction"
Reading physical model inputs from file "physics.inp".
Setting up time integration.
Solving in time (from 0 to 400 iterations)
Writing solution file op_00000.dat.
Iteration: 10 Time: 2.500E-02 Max CFL: 2.000E-01 Max Diff. No.: 0.000E+00 Norm: 1.1107E-02 Conservation loss: 3.7297E-17
Iteration: 20 Time: 5.000E-02 Max CFL: 2.000E-01 Max Diff. No.: 0.000E+00 Norm: 1.1107E-02 Conservation loss: 5.9414E-17
Iteration: 30 Time: 7.500E-02 Max CFL: 2.000E-01 Max Diff. No.: 0.000E+00 Norm: 1.1107E-02 Conservation loss: 2.6455E-17
Iteration: 40 Time: 1.000E-01 Max CFL: 2.000E-01 Max Diff. No.: 0.000E+00 Norm: 1.1107E-02 Conservation loss: 2.0340E-16
Writing solution file op_00001.dat.
Iteration: 50 Time: 1.250E-01 Max CFL: 2.000E-01 Max Diff. No.: 0.000E+00 Norm: 1.1107E-02 Conservation loss: 6.8088E-17
Iteration: 60 Time: 1.500E-01 Max CFL: 2.000E-01 Max Diff. No.: 0.000E+00 Norm: 1.1107E-02 Conservation loss: 6.1149E-17
Iteration: 70 Time: 1.750E-01 Max CFL: 2.000E-01 Max Diff. No.: 0.000E+00 Norm: 1.1107E-02 Conservation loss: 6.1149E-17
Iteration: 80 Time: 2.000E-01 Max CFL: 2.000E-01 Max Diff. No.: 0.000E+00 Norm: 1.1107E-02 Conservation loss: 9.0639E-17
Writing solution file op_00002.dat.
Iteration: 90 Time: 2.250E-01 Max CFL: 2.000E-01 Max Diff. No.: 0.000E+00 Norm: 1.1107E-02 Conservation loss: 2.9924E-17
Iteration: 100 Time: 2.500E-01 Max CFL: 2.000E-01 Max Diff. No.: 0.000E+00 Norm: 1.1107E-02 Conservation loss: 6.5052E-18
Iteration: 110 Time: 2.750E-01 Max CFL: 2.000E-01 Max Diff. No.: 0.000E+00 Norm: 1.1107E-02 Conservation loss: 9.2374E-17
Iteration: 120 Time: 3.000E-01 Max CFL: 2.000E-01 Max Diff. No.: 0.000E+00 Norm: 1.1107E-02 Conservation loss: 9.2374E-17
Writing solution file op_00003.dat.
Iteration: 130 Time: 3.250E-01 Max CFL: 2.000E-01 Max Diff. No.: 0.000E+00 Norm: 1.1107E-02 Conservation loss: 2.9057E-17
Iteration: 140 Time: 3.500E-01 Max CFL: 2.000E-01 Max Diff. No.: 0.000E+00 Norm: 1.1107E-02 Conservation loss: 1.6046E-17
Iteration: 150 Time: 3.750E-01 Max CFL: 2.000E-01 Max Diff. No.: 0.000E+00 Norm: 1.1107E-02 Conservation loss: 9.1073E-18
Iteration: 160 Time: 4.000E-01 Max CFL: 2.000E-01 Max Diff. No.: 0.000E+00 Norm: 1.1107E-02 Conservation loss: 1.2620E-16
Writing solution file op_00004.dat.
Iteration: 170 Time: 4.250E-01 Max CFL: 2.000E-01 Max Diff. No.: 0.000E+00 Norm: 1.1107E-02 Conservation loss: 6.1149E-17
Iteration: 180 Time: 4.500E-01 Max CFL: 2.000E-01 Max Diff. No.: 0.000E+00 Norm: 1.1107E-02 Conservation loss: 2.0296E-16
Iteration: 190 Time: 4.750E-01 Max CFL: 2.000E-01 Max Diff. No.: 0.000E+00 Norm: 1.1107E-02 Conservation loss: 2.6021E-17
Iteration: 200 Time: 5.000E-01 Max CFL: 2.000E-01 Max Diff. No.: 0.000E+00 Norm: 1.1107E-02 Conservation loss: 2.0383E-17
Writing solution file op_00005.dat.
Iteration: 210 Time: 5.250E-01 Max CFL: 2.000E-01 Max Diff. No.: 0.000E+00 Norm: 1.1107E-02 Conservation loss: 3.7730E-17
Iteration: 220 Time: 5.500E-01 Max CFL: 2.000E-01 Max Diff. No.: 0.000E+00 Norm: 1.1107E-02 Conservation loss: 3.4261E-17
Iteration: 230 Time: 5.750E-01 Max CFL: 2.000E-01 Max Diff. No.: 0.000E+00 Norm: 1.1107E-02 Conservation loss: 1.4528E-16
Iteration: 240 Time: 6.000E-01 Max CFL: 2.000E-01 Max Diff. No.: 0.000E+00 Norm: 1.1107E-02 Conservation loss: 4.3802E-17
Writing solution file op_00006.dat.
Iteration: 250 Time: 6.250E-01 Max CFL: 2.000E-01 Max Diff. No.: 0.000E+00 Norm: 1.1107E-02 Conservation loss: 2.1684E-18
Iteration: 260 Time: 6.500E-01 Max CFL: 2.000E-01 Max Diff. No.: 0.000E+00 Norm: 1.1107E-02 Conservation loss: 8.2833E-17
Iteration: 270 Time: 6.750E-01 Max CFL: 2.000E-01 Max Diff. No.: 0.000E+00 Norm: 1.1107E-02 Conservation loss: 1.4528E-16
Iteration: 280 Time: 7.000E-01 Max CFL: 2.000E-01 Max Diff. No.: 0.000E+00 Norm: 1.1107E-02 Conservation loss: 5.8547E-17
Writing solution file op_00007.dat.
Iteration: 290 Time: 7.250E-01 Max CFL: 2.000E-01 Max Diff. No.: 0.000E+00 Norm: 1.1107E-02 Conservation loss: 1.3141E-16
Iteration: 300 Time: 7.500E-01 Max CFL: 2.000E-01 Max Diff. No.: 0.000E+00 Norm: 1.1107E-02 Conservation loss: 1.1232E-16
Iteration: 310 Time: 7.750E-01 Max CFL: 2.000E-01 Max Diff. No.: 0.000E+00 Norm: 1.1107E-02 Conservation loss: 8.8037E-17
Iteration: 320 Time: 8.000E-01 Max CFL: 2.000E-01 Max Diff. No.: 0.000E+00 Norm: 1.1107E-02 Conservation loss: 5.6812E-17
Writing solution file op_00008.dat.
Iteration: 330 Time: 8.250E-01 Max CFL: 2.000E-01 Max Diff. No.: 0.000E+00 Norm: 1.1107E-02 Conservation loss: 3.2526E-17
Iteration: 340 Time: 8.500E-01 Max CFL: 2.000E-01 Max Diff. No.: 0.000E+00 Norm: 1.1107E-02 Conservation loss: 3.5996E-17
Iteration: 350 Time: 8.750E-01 Max CFL: 2.000E-01 Max Diff. No.: 0.000E+00 Norm: 1.1107E-02 Conservation loss: 1.9516E-17
Iteration: 360 Time: 9.000E-01 Max CFL: 2.000E-01 Max Diff. No.: 0.000E+00 Norm: 1.1107E-02 Conservation loss: 2.5587E-17
Writing solution file op_00009.dat.
Iteration: 370 Time: 9.250E-01 Max CFL: 2.000E-01 Max Diff. No.: 0.000E+00 Norm: 1.1107E-02 Conservation loss: 4.2934E-17
Iteration: 380 Time: 9.500E-01 Max CFL: 2.000E-01 Max Diff. No.: 0.000E+00 Norm: 1.1107E-02 Conservation loss: 3.2526E-17
Iteration: 390 Time: 9.750E-01 Max CFL: 2.000E-01 Max Diff. No.: 0.000E+00 Norm: 1.1107E-02 Conservation loss: 2.2768E-17
Iteration: 400 Time: 1.000E+00 Max CFL: 2.000E-01 Max Diff. No.: 0.000E+00 Norm: 1.1107E-02 Conservation loss: 2.2118E-17
Writing solution file op_00010.dat.
Completed time integration (Final time: 1.000000).
Reading array from ASCII file exact.inp (Serial mode).
Computed errors:
L1 Error : 1.0521708205329536E-06
L2 Error : 1.0871437024745659E-06
Linfinity Error : 1.3438402750587386E-06
Conservation Errors:
2.2117724318704290E-17
Solver runtime (in seconds): 9.4072000000000003E-02
Total runtime (in seconds): 9.4830999999999999E-02
Deallocating arrays.
Finished.