1D Linear Advection - Discontinuous Waves
Location: hypar/Examples/1D/LinearAdvection/DiscontinuousWaves (This directory contains all the input files needed to run this case. If there is a Run.m, run it in MATLAB to quickly set up, run, and visualize the example).
Governing equations: 1D Linear Advection Equation (linearadr.h)
References:
- Ghosh, D., Baeder, J. D., "Compact Reconstruction Schemes with Weighted ENO Limiting for Hyperbolic Conservation Laws", SIAM Journal on Scientific Computing, 34 (3), 2012, A1678–A1706
Domain: \(-1 \le x \le 1\), "periodic" (_PERIODIC_) boundary conditions
Initial solution:
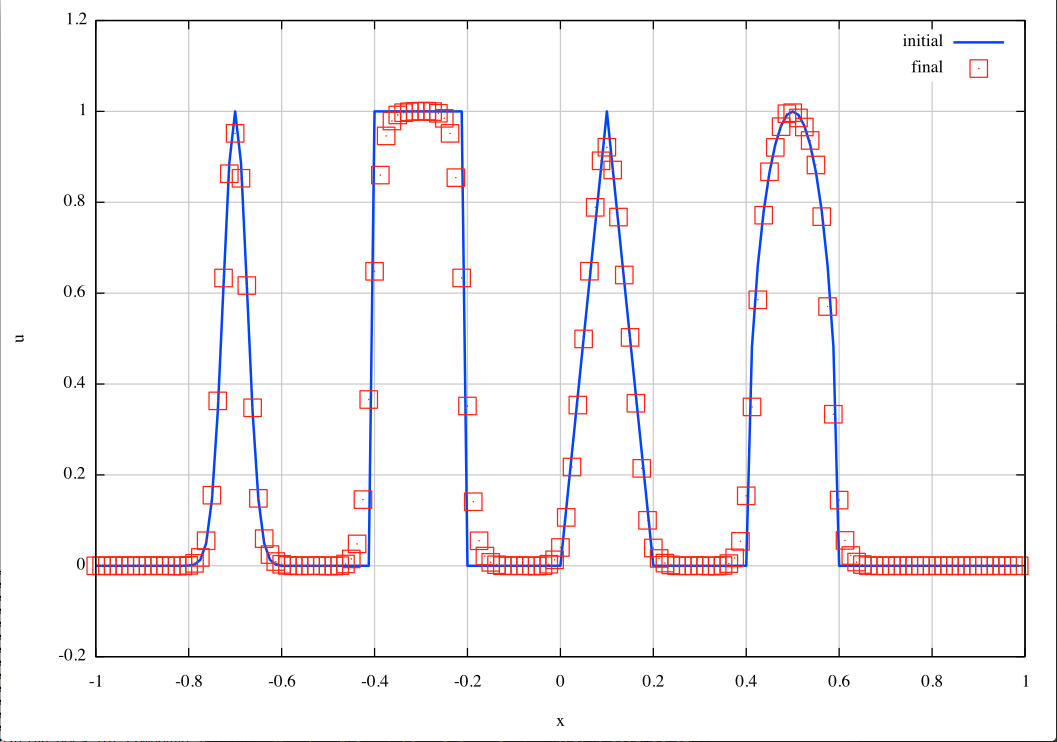
\begin{equation} u\left(x,0\right) = \left\{\begin{array}{lc} \exp\left(-\log\left(2\right)\frac{\left(x+7\right)^2}{0.0009}\right) & -0.8\le x \le -0.6 \\ 1 & -0.4\le x \le -0.2 \\ 1 - \left|10\left(x-0.1\right)\right| & 0\le x \le 0.2 \\ \sqrt{1-100\left(x-0.5\right)^2} & 0.4\le x \le 0.6 \\ 0 & {\rm otherwise} \end{array}\right. \end{equation}
Numerical Method:
- Spatial discretization (hyperbolic): 5th order CRWENO (Interp1PrimFifthOrderCRWENO())
- Time integration: SSPRK3 (TimeRK(), _RK_SSP3_)
Input files required:
solver.inp
begin
ndims 1
nvars 1
size 160
iproc 1
ghost 3
n_iter 800
time_scheme rk
time_scheme_type ssprk3
hyp_space_scheme crweno5
dt 0.0025
screen_op_iter 10
file_op_iter 99999
ip_file_type ascii
op_file_format text
op_overwrite no
model linear-advection-diffusion-reaction
end
boundary.inp
2
periodic 0 1 0 0
periodic 0 -1 0 0
physics.inp
begin
advection 1.0
end
lusolver.inp (optional)
begin
reducedsolvetype jacobi
evaluate_norm 1
maxiter 10
atol 1e-12
rtol 1e-10
verbose 0
end
weno.inp (optional)
begin
mapped 1
borges 0
yc 0
no_limiting 0
epsilon 0.000001
p 2.0
rc 0.3
xi 0.001
end
To generate initial.inp, compile and run the following code in the run directory. Note: if the final time is an integer multiple of the time period, the file initial.inp can also be used as the exact solution exact.inp (i.e. create a sym link called exact.inp pointing to initial.inp, or just copy initial.inp to exact.inp).
#include <stdio.h>
#include <stdlib.h>
#include <math.h>
#include <string.h>
{
return (x<0? -x : x);
}
int main(){
int NI,ndims;
char ip_file_type[50];
strcpy(ip_file_type,"ascii");
FILE *in;
printf("Reading file \"solver.inp\"...\n");
in = fopen("solver.inp","r");
if (!in) printf("Error: Input file \"solver.inp\" not found. Default values will be used.\n");
else {
char word[500];
fscanf(in,"%s",word);
if (!strcmp(word, "begin")){
while (strcmp(word, "end")){
fscanf(in,"%s",word);
if (!strcmp(word, "ndims")) fscanf(in,"%d",&ndims);
else if (!strcmp(word, "size")) fscanf(in,"%d",&NI);
else if (!strcmp(word, "ip_file_type")) fscanf(in,"%s",ip_file_type);
}
} else printf("Error: Illegal format in solver.inp. Crash and burn!\n");
}
fclose(in);
if (ndims != 1) {
printf("ndims is not 1 in solver.inp. this code is to generate 1D initial conditions\n");
return(0);
}
printf("Grid:\t\t\t%d\n",NI);
int i;
double dx = 2.0 / ((double)NI);
double *x, *u;
x = (double*) calloc (NI, sizeof(double));
u = (double*) calloc (NI, sizeof(double));
for (i = 0; i < NI; i++){
x[i] = -1.0 + i*dx;
if (x[i] < -0.8) u[i] = 0.0;
else if (x[i] < -0.6) u[i] = exp(-log(2.0)*(x[i]+0.7)*(x[i]+0.7)/0.0009);
else if (x[i] < -0.4) u[i] = 0.0;
else if (x[i] < -0.2) u[i] = 1.0;
else if (x[i] < 0 ) u[i] = 0.0;
else if (x[i] < 0.4) u[i] = 0.0;
else if (x[i] < 0.6) u[i] = sqrt(1.0-100*(x[i]-0.5)*(x[i]-0.5));
else u[i] = 0.0;
}
FILE *out;
if (!strcmp(ip_file_type,"ascii")) {
printf("Writing ASCII initial solution file initial.inp\n");
out = fopen("initial.inp","w");
for (i = 0; i < NI; i++) fprintf(out,"%lf ",x[i]);
fprintf(out,"\n");
for (i = 0; i < NI; i++) fprintf(out,"%lf ",u[i]);
fprintf(out,"\n");
fclose(out);
} else if ((!strcmp(ip_file_type,"binary")) || (!strcmp(ip_file_type,"bin"))) {
printf("Writing binary initial solution file initial.inp\n");
out = fopen("initial.inp","wb");
fwrite(x,sizeof(double),NI,out);
fwrite(u,sizeof(double),NI,out);
fclose(out);
}
free(x);
free(u);
return(0);
}
Output:
After running the code, there should be two solution output files op_00000.dat and op_00001.dat; the first one is the initial solution, and the latter is the final solution. Both these files are ASCII text (HyPar::op_file_format is set to text in solver.inp).
Final solution at t=2.0: The following figure is obtained by plotting op_00000.dat (initial) and op_00001.dat (final). In both these files, the first column is grid index, the second column is x-coordinate, and the third column is the solution.
Expected screen output:
HyPar - Parallel (MPI) version with 1 processes
Compiled with PETSc time integration.
Reading solver inputs from file "solver.inp".
No. of dimensions : 1
No. of variables : 1
Domain size : 160
Processes along each dimension : 1
No. of ghosts pts : 3
No. of iter. : 800
Restart iteration : 0
Time integration scheme : rk (ssprk3)
Spatial discretization scheme (hyperbolic) : crweno5
Split hyperbolic flux term? : no
Interpolation type for hyperbolic term : characteristic
Spatial discretization type (parabolic ) : nonconservative-1stage
Spatial discretization scheme (parabolic ) : 2
Time Step : 2.500000E-03
Check for conservation : no
Screen output iterations : 10
File output iterations : 99999
Initial solution file type : ascii
Initial solution read mode : serial
Solution file write mode : serial
Solution file format : text
Overwrite solution file : no
Physical model : linear-advection-diffusion-reaction
Partitioning domain.
Allocating data arrays.
Reading array from ASCII file initial.inp (Serial mode).
Volume integral of the initial solution:
0: 5.1835172499999993E-01
Reading boundary conditions from "boundary.inp".
Boundary periodic: Along dimension 0 and face +1
Boundary periodic: Along dimension 0 and face -1
2 boundary condition(s) read.
Initializing solvers.
Reading WENO parameters from weno.inp.
Initializing physics. Model = "linear-advection-diffusion-reaction"
Reading physical model inputs from file "physics.inp".
Setting up time integration.
Solving in time (from 0 to 800 iterations)
Writing solution file op_00000.dat.
Iteration: 10 Time: 2.500E-02 Max CFL: 2.000E-01 Max Diff. No.: 0.000E+00 Norm: 2.2256E-02
Iteration: 20 Time: 5.000E-02 Max CFL: 2.000E-01 Max Diff. No.: 0.000E+00 Norm: 2.1583E-02
Iteration: 30 Time: 7.500E-02 Max CFL: 2.000E-01 Max Diff. No.: 0.000E+00 Norm: 2.1179E-02
Iteration: 40 Time: 1.000E-01 Max CFL: 2.000E-01 Max Diff. No.: 0.000E+00 Norm: 2.0887E-02
Iteration: 50 Time: 1.250E-01 Max CFL: 2.000E-01 Max Diff. No.: 0.000E+00 Norm: 2.0660E-02
Iteration: 60 Time: 1.500E-01 Max CFL: 2.000E-01 Max Diff. No.: 0.000E+00 Norm: 2.0475E-02
Iteration: 70 Time: 1.750E-01 Max CFL: 2.000E-01 Max Diff. No.: 0.000E+00 Norm: 2.0320E-02
Iteration: 80 Time: 2.000E-01 Max CFL: 2.000E-01 Max Diff. No.: 0.000E+00 Norm: 2.0187E-02
Iteration: 90 Time: 2.250E-01 Max CFL: 2.000E-01 Max Diff. No.: 0.000E+00 Norm: 2.0071E-02
Iteration: 100 Time: 2.500E-01 Max CFL: 2.000E-01 Max Diff. No.: 0.000E+00 Norm: 1.9968E-02
Iteration: 110 Time: 2.750E-01 Max CFL: 2.000E-01 Max Diff. No.: 0.000E+00 Norm: 1.9877E-02
Iteration: 120 Time: 3.000E-01 Max CFL: 2.000E-01 Max Diff. No.: 0.000E+00 Norm: 1.9794E-02
Iteration: 130 Time: 3.250E-01 Max CFL: 2.000E-01 Max Diff. No.: 0.000E+00 Norm: 1.9719E-02
Iteration: 140 Time: 3.500E-01 Max CFL: 2.000E-01 Max Diff. No.: 0.000E+00 Norm: 1.9650E-02
Iteration: 150 Time: 3.750E-01 Max CFL: 2.000E-01 Max Diff. No.: 0.000E+00 Norm: 1.9587E-02
Iteration: 160 Time: 4.000E-01 Max CFL: 2.000E-01 Max Diff. No.: 0.000E+00 Norm: 1.9522E-02
Iteration: 170 Time: 4.250E-01 Max CFL: 2.000E-01 Max Diff. No.: 0.000E+00 Norm: 1.9462E-02
Iteration: 180 Time: 4.500E-01 Max CFL: 2.000E-01 Max Diff. No.: 0.000E+00 Norm: 1.9412E-02
Iteration: 190 Time: 4.750E-01 Max CFL: 2.000E-01 Max Diff. No.: 0.000E+00 Norm: 1.9364E-02
Iteration: 200 Time: 5.000E-01 Max CFL: 2.000E-01 Max Diff. No.: 0.000E+00 Norm: 1.9319E-02
Iteration: 210 Time: 5.250E-01 Max CFL: 2.000E-01 Max Diff. No.: 0.000E+00 Norm: 1.9276E-02
Iteration: 220 Time: 5.500E-01 Max CFL: 2.000E-01 Max Diff. No.: 0.000E+00 Norm: 1.9235E-02
Iteration: 230 Time: 5.750E-01 Max CFL: 2.000E-01 Max Diff. No.: 0.000E+00 Norm: 1.9191E-02
Iteration: 240 Time: 6.000E-01 Max CFL: 2.000E-01 Max Diff. No.: 0.000E+00 Norm: 1.9152E-02
Iteration: 250 Time: 6.250E-01 Max CFL: 2.000E-01 Max Diff. No.: 0.000E+00 Norm: 1.9117E-02
Iteration: 260 Time: 6.500E-01 Max CFL: 2.000E-01 Max Diff. No.: 0.000E+00 Norm: 1.9084E-02
Iteration: 270 Time: 6.750E-01 Max CFL: 2.000E-01 Max Diff. No.: 0.000E+00 Norm: 1.9052E-02
Iteration: 280 Time: 7.000E-01 Max CFL: 2.000E-01 Max Diff. No.: 0.000E+00 Norm: 1.9022E-02
Iteration: 290 Time: 7.250E-01 Max CFL: 2.000E-01 Max Diff. No.: 0.000E+00 Norm: 1.8992E-02
Iteration: 300 Time: 7.500E-01 Max CFL: 2.000E-01 Max Diff. No.: 0.000E+00 Norm: 1.8964E-02
Iteration: 310 Time: 7.750E-01 Max CFL: 2.000E-01 Max Diff. No.: 0.000E+00 Norm: 1.8936E-02
Iteration: 320 Time: 8.000E-01 Max CFL: 2.000E-01 Max Diff. No.: 0.000E+00 Norm: 1.8910E-02
Iteration: 330 Time: 8.250E-01 Max CFL: 2.000E-01 Max Diff. No.: 0.000E+00 Norm: 1.8884E-02
Iteration: 340 Time: 8.500E-01 Max CFL: 2.000E-01 Max Diff. No.: 0.000E+00 Norm: 1.8859E-02
Iteration: 350 Time: 8.750E-01 Max CFL: 2.000E-01 Max Diff. No.: 0.000E+00 Norm: 1.8835E-02
Iteration: 360 Time: 9.000E-01 Max CFL: 2.000E-01 Max Diff. No.: 0.000E+00 Norm: 1.8811E-02
Iteration: 370 Time: 9.250E-01 Max CFL: 2.000E-01 Max Diff. No.: 0.000E+00 Norm: 1.8788E-02
Iteration: 380 Time: 9.500E-01 Max CFL: 2.000E-01 Max Diff. No.: 0.000E+00 Norm: 1.8766E-02
Iteration: 390 Time: 9.750E-01 Max CFL: 2.000E-01 Max Diff. No.: 0.000E+00 Norm: 1.8745E-02
Iteration: 400 Time: 1.000E+00 Max CFL: 2.000E-01 Max Diff. No.: 0.000E+00 Norm: 1.8724E-02
Iteration: 410 Time: 1.025E+00 Max CFL: 2.000E-01 Max Diff. No.: 0.000E+00 Norm: 1.8704E-02
Iteration: 420 Time: 1.050E+00 Max CFL: 2.000E-01 Max Diff. No.: 0.000E+00 Norm: 1.8684E-02
Iteration: 430 Time: 1.075E+00 Max CFL: 2.000E-01 Max Diff. No.: 0.000E+00 Norm: 1.8665E-02
Iteration: 440 Time: 1.100E+00 Max CFL: 2.000E-01 Max Diff. No.: 0.000E+00 Norm: 1.8647E-02
Iteration: 450 Time: 1.125E+00 Max CFL: 2.000E-01 Max Diff. No.: 0.000E+00 Norm: 1.8628E-02
Iteration: 460 Time: 1.150E+00 Max CFL: 2.000E-01 Max Diff. No.: 0.000E+00 Norm: 1.8610E-02
Iteration: 470 Time: 1.175E+00 Max CFL: 2.000E-01 Max Diff. No.: 0.000E+00 Norm: 1.8594E-02
Iteration: 480 Time: 1.200E+00 Max CFL: 2.000E-01 Max Diff. No.: 0.000E+00 Norm: 1.8568E-02
Iteration: 490 Time: 1.225E+00 Max CFL: 2.000E-01 Max Diff. No.: 0.000E+00 Norm: 1.8549E-02
Iteration: 500 Time: 1.250E+00 Max CFL: 2.000E-01 Max Diff. No.: 0.000E+00 Norm: 1.8534E-02
Iteration: 510 Time: 1.275E+00 Max CFL: 2.000E-01 Max Diff. No.: 0.000E+00 Norm: 1.8519E-02
Iteration: 520 Time: 1.300E+00 Max CFL: 2.000E-01 Max Diff. No.: 0.000E+00 Norm: 1.8504E-02
Iteration: 530 Time: 1.325E+00 Max CFL: 2.000E-01 Max Diff. No.: 0.000E+00 Norm: 1.8489E-02
Iteration: 540 Time: 1.350E+00 Max CFL: 2.000E-01 Max Diff. No.: 0.000E+00 Norm: 1.8474E-02
Iteration: 550 Time: 1.375E+00 Max CFL: 2.000E-01 Max Diff. No.: 0.000E+00 Norm: 1.8460E-02
Iteration: 560 Time: 1.400E+00 Max CFL: 2.000E-01 Max Diff. No.: 0.000E+00 Norm: 1.8438E-02
Iteration: 570 Time: 1.425E+00 Max CFL: 2.000E-01 Max Diff. No.: 0.000E+00 Norm: 1.8422E-02
Iteration: 580 Time: 1.450E+00 Max CFL: 2.000E-01 Max Diff. No.: 0.000E+00 Norm: 1.8409E-02
Iteration: 590 Time: 1.475E+00 Max CFL: 2.000E-01 Max Diff. No.: 0.000E+00 Norm: 1.8396E-02
Iteration: 600 Time: 1.500E+00 Max CFL: 2.000E-01 Max Diff. No.: 0.000E+00 Norm: 1.8383E-02
Iteration: 610 Time: 1.525E+00 Max CFL: 2.000E-01 Max Diff. No.: 0.000E+00 Norm: 1.8369E-02
Iteration: 620 Time: 1.550E+00 Max CFL: 2.000E-01 Max Diff. No.: 0.000E+00 Norm: 1.8356E-02
Iteration: 630 Time: 1.575E+00 Max CFL: 2.000E-01 Max Diff. No.: 0.000E+00 Norm: 1.8343E-02
Iteration: 640 Time: 1.600E+00 Max CFL: 2.000E-01 Max Diff. No.: 0.000E+00 Norm: 1.8330E-02
Iteration: 650 Time: 1.625E+00 Max CFL: 2.000E-01 Max Diff. No.: 0.000E+00 Norm: 1.8318E-02
Iteration: 660 Time: 1.650E+00 Max CFL: 2.000E-01 Max Diff. No.: 0.000E+00 Norm: 1.8304E-02
Iteration: 670 Time: 1.675E+00 Max CFL: 2.000E-01 Max Diff. No.: 0.000E+00 Norm: 1.8291E-02
Iteration: 680 Time: 1.700E+00 Max CFL: 2.000E-01 Max Diff. No.: 0.000E+00 Norm: 1.8275E-02
Iteration: 690 Time: 1.725E+00 Max CFL: 2.000E-01 Max Diff. No.: 0.000E+00 Norm: 1.8263E-02
Iteration: 700 Time: 1.750E+00 Max CFL: 2.000E-01 Max Diff. No.: 0.000E+00 Norm: 1.8250E-02
Iteration: 710 Time: 1.775E+00 Max CFL: 2.000E-01 Max Diff. No.: 0.000E+00 Norm: 1.8238E-02
Iteration: 720 Time: 1.800E+00 Max CFL: 2.000E-01 Max Diff. No.: 0.000E+00 Norm: 1.8227E-02
Iteration: 730 Time: 1.825E+00 Max CFL: 2.000E-01 Max Diff. No.: 0.000E+00 Norm: 1.8215E-02
Iteration: 740 Time: 1.850E+00 Max CFL: 2.000E-01 Max Diff. No.: 0.000E+00 Norm: 1.8204E-02
Iteration: 750 Time: 1.875E+00 Max CFL: 2.000E-01 Max Diff. No.: 0.000E+00 Norm: 1.8192E-02
Iteration: 760 Time: 1.900E+00 Max CFL: 2.000E-01 Max Diff. No.: 0.000E+00 Norm: 1.8181E-02
Iteration: 770 Time: 1.925E+00 Max CFL: 2.000E-01 Max Diff. No.: 0.000E+00 Norm: 1.8170E-02
Iteration: 780 Time: 1.950E+00 Max CFL: 2.000E-01 Max Diff. No.: 0.000E+00 Norm: 1.8159E-02
Iteration: 790 Time: 1.975E+00 Max CFL: 2.000E-01 Max Diff. No.: 0.000E+00 Norm: 1.8148E-02
Iteration: 800 Time: 2.000E+00 Max CFL: 2.000E-01 Max Diff. No.: 0.000E+00 Norm: 1.8137E-02
Writing solution file op_00001.dat.
Completed time integration (Final time: 2.000000).
Reading array from ASCII file exact.inp (Serial mode).
Computed errors:
L1 Error : 9.6315813130322420E-02
L2 Error : 1.4404939573799375E-01
Linfinity Error : 3.6645294456728839E-01
Conservation Errors:
0.0000000000000000E+00
Solver runtime (in seconds): 3.3181800000000000E-01
Total runtime (in seconds): 3.3263100000000001E-01
Deallocating arrays.
Finished.