HyPar  1.0
Finite-Difference Hyperbolic-Parabolic PDE Solver on Cartesian Grids
1D Euler Equations - Shu-Osher Problem

Description:

Location: hypar/Examples/1D/Euler1D/ShuOsherProblem (This directory contains all the input files needed to run this case. If there is a Run.m, run it in MATLAB to quickly set up, run, and visualize the example).

Governing equations: 1D Euler equations (euler1d.h)

References:

  • C.-W. Shu and S. Osher, "Efficient implementation of essentially non-oscillatory schemes ,II," J. Comput. Phys., 83 (1989), pp. 32–78

Domain: \(-5 \le x \le 5\), "extrapolate" (_EXTRAPOLATE_) boundary conditions

Initial Solution:

  • \( -5 \le x < -4\): \(\rho = 27/7, u = 4\sqrt{35}/7, p = 31/3\)
  • \( -4 \le x \le 5\): \(\rho = 1 + 0.2\sin\left(5x\right), u = 0, p = 1\)

Numerical Method:

Input files required:

solver.inp:

begin
ndims 1
nvars 3
size 201
iproc 1
ghost 3
n_iter 180
time_scheme rk
time_scheme_type 44
hyp_space_scheme weno5
hyp_interp_type characteristic
conservation_check yes
dt 0.01
screen_op_iter 10
file_op_iter 9999
op_file_format text
op_overwrite no
model euler1d
end

boundary.inp

2
extrapolate 0 1 0 0
extrapolate 0 -1 0 0

physics.inp

begin
gamma 1.4
upwinding rf-char
end

weno.inp (optional)

begin
mapped 1
borges 0
yc 0
no_limiting 0
epsilon 0.000001
p 2.0
rc 0.3
xi 0.001
end

To generate initial.inp, compile and run the following code in the run directory:

#include <stdio.h>
#include <stdlib.h>
#include <math.h>
#include <string.h>
int main(){
int NI=101,ndims=1;
FILE *in;
char ip_file_type[50];
strcpy(ip_file_type,"ascii");
printf("Reading file \"solver.inp\"...\n");
in = fopen("solver.inp","r");
if (!in) {
printf("Error: Input file \"solver.inp\" not found. Default values will be used.\n");
} else {
char word[500];
fscanf(in,"%s",word);
if (!strcmp(word, "begin")){
while (strcmp(word, "end")){
fscanf(in,"%s",word);
if (!strcmp(word, "ndims")) fscanf(in,"%d",&ndims);
else if (!strcmp(word, "size")) fscanf(in,"%d",&NI);
else if (!strcmp(word, "ip_file_type")) fscanf(in,"%s",ip_file_type);
}
} else {
printf("Error: Illegal format in solver.inp. Crash and burn!\n");
}
}
fclose(in);
if (ndims != 1) {
printf("ndims is not 1 in solver.inp. this code is to generate 1D initial conditions\n");
return(0);
}
printf("Grid:\t\t\t%d\n",NI);
int i;
double dx = 10.0 / ((double)(NI-1));
double *x, *rho,*rhou,*e;
x = (double*) calloc (NI, sizeof(double));
rho = (double*) calloc (NI, sizeof(double));
rhou = (double*) calloc (NI, sizeof(double));
e = (double*) calloc (NI, sizeof(double));
for (i = 0; i < NI; i++){
x[i] = -5.0 + i*dx;
double RHO,U,P;
if (x[i] < -4.0) {
RHO = 27.0/7.0;
U = 4.0*sqrt(35.0)/9.0;
P = 31.0/3.0;
} else {
RHO = 1.0+0.2*sin(5*x[i]);
U = 0;
P = 1;
}
rho[i] = RHO;
rhou[i] = RHO*U;
e[i] = P/0.4 + 0.5*RHO*U*U;
}
if (!strcmp(ip_file_type,"ascii")) {
FILE *out;
out = fopen("initial.inp","w");
for (i = 0; i < NI; i++) fprintf(out,"%lf ",x[i]);
fprintf(out,"\n");
for (i = 0; i < NI; i++) fprintf(out,"%lf ",rho[i]);
fprintf(out,"\n");
for (i = 0; i < NI; i++) fprintf(out,"%lf ",rhou[i]);
fprintf(out,"\n");
for (i = 0; i < NI; i++) fprintf(out,"%lf ",e[i]);
fprintf(out,"\n");
fclose(out);
} else if ((!strcmp(ip_file_type,"binary")) || (!strcmp(ip_file_type,"bin"))) {
printf("Error: Writing binary initial solution file not implemented. ");
printf("Please choose ip_file_type in solver.inp as \"ascii\".\n");
}
free(x);
free(rho);
free(rhou);
free(e);
return(0);
}

Output:

After running the code, there should be two solution output files op_00000.dat and op_00001.dat; the first one is the initial solution, and the latter is the final solution. Both these files are ASCII text (HyPar::op_file_format is set to text in solver.inp). In these files, the first column is grid index, the second column is x-coordinate, and the remaining columns are the solution components.

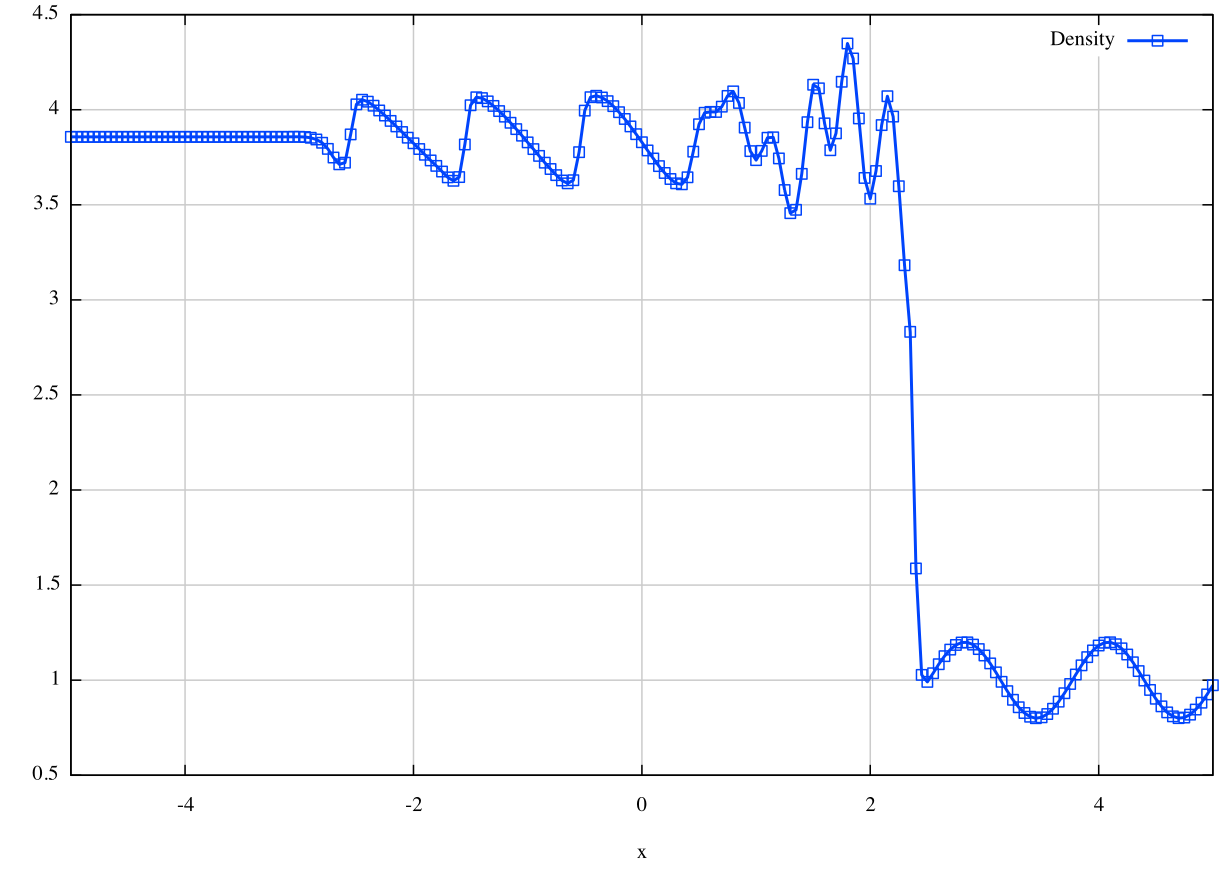
Final solution at t=1.8: The following figure is obtained by plotting op_00001.dat. Note that the output is in terms of the conserved variables, so they have to converted to the primitive variables (density, velocity, and pressure).

Solution_1DShuOsherProblem.png

Since HyPar::ConservationCheck is set to yes in solver.inp, the code checks for conservation error and prints it to screen, as well as the file conservation.dat:

201 1 1.0000000000000000E-02 1.7930858824116804E-15 2.6272672109858204E-15 2.4147912130226402E-15

The numbers are: number of grid points (HyPar::dim_global), number of processors (MPIVariables::iproc), time step size (HyPar::dt), and conservation error (HyPar::ConservationError) for each component.

Expected screen output:

HyPar - Parallel (MPI) version with 1 processes
Compiled with PETSc time integration.
Reading solver inputs from file "solver.inp".
No. of dimensions : 1
No. of variables : 3
Domain size : 201
Processes along each dimension : 1
No. of ghosts pts : 3
No. of iter. : 180
Restart iteration : 0
Time integration scheme : rk (44)
Spatial discretization scheme (hyperbolic) : weno5
Split hyperbolic flux term? : no
Interpolation type for hyperbolic term : characteristic
Spatial discretization type (parabolic ) : nonconservative-1stage
Spatial discretization scheme (parabolic ) : 2
Time Step : 1.000000E-02
Check for conservation : yes
Screen output iterations : 10
File output iterations : 9999
Initial solution file type : ascii
Initial solution read mode : serial
Solution file write mode : serial
Solution file format : text
Overwrite solution file : no
Physical model : euler1d
Partitioning domain.
Allocating data arrays.
Reading array from ASCII file initial.inp (Serial mode).
Volume integral of the initial solution:
0: 1.2878713250000002E+01
1: 1.0141851000000001E+01
2: 6.1791666999999997E+01
Reading boundary conditions from "boundary.inp".
Boundary extrapolate: Along dimension 0 and face +1
Boundary extrapolate: Along dimension 0 and face -1
2 boundary condition(s) read.
Initializing solvers.
Reading WENO parameters from weno.inp.
Initializing physics. Model = "euler1d"
Reading physical model inputs from file "physics.inp".
Setting up time integration.
Solving in time (from 0 to 180 iterations)
Writing solution file op_00000.dat.
Iteration: 10 Time: 1.000E-01 Max CFL: 9.364E-01 Max Diff. No.: -1.000E+00 Norm: 1.1915E+00 Conservation loss: 2.0952E-16
Iteration: 20 Time: 2.000E-01 Max CFL: 9.331E-01 Max Diff. No.: -1.000E+00 Norm: 1.2028E+00 Conservation loss: 6.0450E-16
Iteration: 30 Time: 3.000E-01 Max CFL: 9.336E-01 Max Diff. No.: -1.000E+00 Norm: 1.1819E+00 Conservation loss: 5.4325E-16
Iteration: 40 Time: 4.000E-01 Max CFL: 9.371E-01 Max Diff. No.: -1.000E+00 Norm: 1.1560E+00 Conservation loss: 9.1589E-16
Iteration: 50 Time: 5.000E-01 Max CFL: 9.404E-01 Max Diff. No.: -1.000E+00 Norm: 1.2418E+00 Conservation loss: 5.5529E-16
Iteration: 60 Time: 6.000E-01 Max CFL: 9.380E-01 Max Diff. No.: -1.000E+00 Norm: 1.2077E+00 Conservation loss: 1.2533E-15
Iteration: 70 Time: 7.000E-01 Max CFL: 9.336E-01 Max Diff. No.: -1.000E+00 Norm: 1.2324E+00 Conservation loss: 1.3792E-15
Iteration: 80 Time: 8.000E-01 Max CFL: 9.392E-01 Max Diff. No.: -1.000E+00 Norm: 1.1441E+00 Conservation loss: 1.7333E-15
Iteration: 90 Time: 9.000E-01 Max CFL: 9.461E-01 Max Diff. No.: -1.000E+00 Norm: 1.2901E+00 Conservation loss: 3.0728E-15
Iteration: 100 Time: 1.000E+00 Max CFL: 9.335E-01 Max Diff. No.: -1.000E+00 Norm: 1.2508E+00 Conservation loss: 3.6711E-15
Iteration: 110 Time: 1.100E+00 Max CFL: 9.392E-01 Max Diff. No.: -1.000E+00 Norm: 1.0874E+00 Conservation loss: 1.9831E-15
Iteration: 120 Time: 1.200E+00 Max CFL: 9.466E-01 Max Diff. No.: -1.000E+00 Norm: 1.2405E+00 Conservation loss: 2.1550E-15
Iteration: 130 Time: 1.300E+00 Max CFL: 9.452E-01 Max Diff. No.: -1.000E+00 Norm: 1.2300E+00 Conservation loss: 5.4132E-15
Iteration: 140 Time: 1.400E+00 Max CFL: 9.402E-01 Max Diff. No.: -1.000E+00 Norm: 1.1943E+00 Conservation loss: 3.1801E-15
Iteration: 150 Time: 1.500E+00 Max CFL: 9.418E-01 Max Diff. No.: -1.000E+00 Norm: 1.1908E+00 Conservation loss: 1.2276E-15
Iteration: 160 Time: 1.600E+00 Max CFL: 9.494E-01 Max Diff. No.: -1.000E+00 Norm: 1.2747E+00 Conservation loss: 5.5747E-15
Iteration: 170 Time: 1.700E+00 Max CFL: 9.359E-01 Max Diff. No.: -1.000E+00 Norm: 1.2182E+00 Conservation loss: 4.8435E-15
Iteration: 180 Time: 1.800E+00 Max CFL: 9.432E-01 Max Diff. No.: -1.000E+00 Norm: 1.1543E+00 Conservation loss: 3.9936E-15
Writing solution file op_00001.dat.
Completed time integration (Final time: 1.800000).
Computed errors:
L1 Error : 0.0000000000000000E+00
L2 Error : 0.0000000000000000E+00
Linfinity Error : 0.0000000000000000E+00
Conservation Errors:
1.7930858824116804E-15
2.6272672109858204E-15
2.4147912130226402E-15
Solver runtime (in seconds): 5.1926499999999998E-01
Total runtime (in seconds): 5.2030600000000005E-01
Deallocating arrays.
Finished.