1D Euler Equations - Sod Shock Tube with Gravitational Force
Description:
Location: hypar/Examples/1D/Euler1D/SodShockTubeWithGravity (This directory contains all the input files needed to run this case. If there is a Run.m, run it in MATLAB to quickly set up, run, and visualize the example).
Governing equations: 1D Euler equations (euler1d.h)
References:
- Xing, Y., Shu, C.-W., "High Order Well-Balanced WENO Scheme for the Gas Dynamics Equations Under Gravitational Fields", Journal of Scientific Computing, 54, 2013, pp. 645-662.
Domain: \(0 \le x \le 1.0\), "slip-wall" (_SLIP_WALL_) boundary conditions (wall velocity is zero), with uniform gravitational force \(g=1\).
Initial Solution:
- \( 0 \le x < 0.5\): \(\rho = 1, u = 0, p = 1\)
- \( 0.5 \le x \le 1\): \(\rho = 0.125, u = 0, p = 0.1\)
Numerical Method:
- Spatial discretization (hyperbolic): Characteristic-based 5th order CRWENO (Interp1PrimFifthOrderCRWENOChar())
- Time integration: RK4 (TimeRK(), _RK_44_)
Input files required:
solver.inp:
begin
ndims 1
nvars 3
size 201
iproc 1
ghost 3
n_iter 200
time_scheme rk
time_scheme_type 44
hyp_space_scheme crweno5
hyp_interp_type characteristic
dt 0.001
screen_op_iter 10
file_op_iter 9999
op_file_format text
op_overwrite no
model euler1d
end
boundary.inp
2
slip-wall 0 1 0 0
0.0
slip-wall 0 -1 0 0
0.0
physics.inp
begin
gamma 1.4
gravity 1.0
upwinding roe
end
To generate initial.inp, compile and run the following code in the run directory:
#include <stdio.h>
#include <stdlib.h>
#include <math.h>
#include <string.h>
int main(){
int NI=101,ndims=1;
FILE *in;
char ip_file_type[50];
strcpy(ip_file_type,"ascii");
printf("Reading file \"solver.inp\"...\n");
in = fopen("solver.inp","r");
if (!in) {
printf("Error: Input file \"solver.inp\" not found. Default values will be used.\n");
} else {
char word[500];
fscanf(in,"%s",word);
if (!strcmp(word, "begin")){
while (strcmp(word, "end")){
fscanf(in,"%s",word);
if (!strcmp(word, "ndims")) fscanf(in,"%d",&ndims);
else if (!strcmp(word, "size")) fscanf(in,"%d",&NI);
else if (!strcmp(word, "ip_file_type")) fscanf(in,"%s",ip_file_type);
}
} else {
printf("Error: Illegal format in solver.inp. Crash and burn!\n");
}
}
fclose(in);
if (ndims != 1) {
printf("ndims is not 1 in solver.inp. this code is to generate 1D initial conditions\n");
return(0);
}
printf("Grid:\t\t\t%d\n",NI);
int i;
double dx = 1.0 / ((double)(NI-1));
double *x, *rho,*rhou,*e;
x = (double*) calloc (NI, sizeof(double));
rho = (double*) calloc (NI, sizeof(double));
rhou = (double*) calloc (NI, sizeof(double));
e = (double*) calloc (NI, sizeof(double));
for (i = 0; i < NI; i++){
x[i] = i*dx;
double RHO,U,P;
if (x[i] < 0.5) {
RHO = 1.0;
U = 0.0;
P = 1.0;
} else {
RHO = 0.125;
U = 0;
P = 0.1;
}
rho[i] = RHO;
rhou[i] = RHO*U;
e[i] = P/0.4 + 0.5*RHO*U*U;
}
if (!strcmp(ip_file_type,"ascii")) {
FILE *out;
out = fopen("initial.inp","w");
for (i = 0; i < NI; i++) fprintf(out,"%lf ",x[i]);
fprintf(out,"\n");
for (i = 0; i < NI; i++) fprintf(out,"%lf ",rho[i]);
fprintf(out,"\n");
for (i = 0; i < NI; i++) fprintf(out,"%lf ",rhou[i]);
fprintf(out,"\n");
for (i = 0; i < NI; i++) fprintf(out,"%lf ",e[i]);
fprintf(out,"\n");
fclose(out);
} else if ((!strcmp(ip_file_type,"binary")) || (!strcmp(ip_file_type,"bin"))) {
printf("Error: Writing binary initial solution file not implemented. ");
printf("Please choose ip_file_type in solver.inp as \"ascii\".\n");
}
free(x);
free(rho);
free(rhou);
free(e);
return(0);
}
Output:
After running the code, there should be two solution output files op_00000.dat and op_00001.dat; the first one is the initial solution, and the latter is the final solution. Both these files are ASCII text (HyPar::op_file_format is set to text in solver.inp). In these files, the first column is grid index, the second column is x-coordinate, and the remaining columns are the solution components.
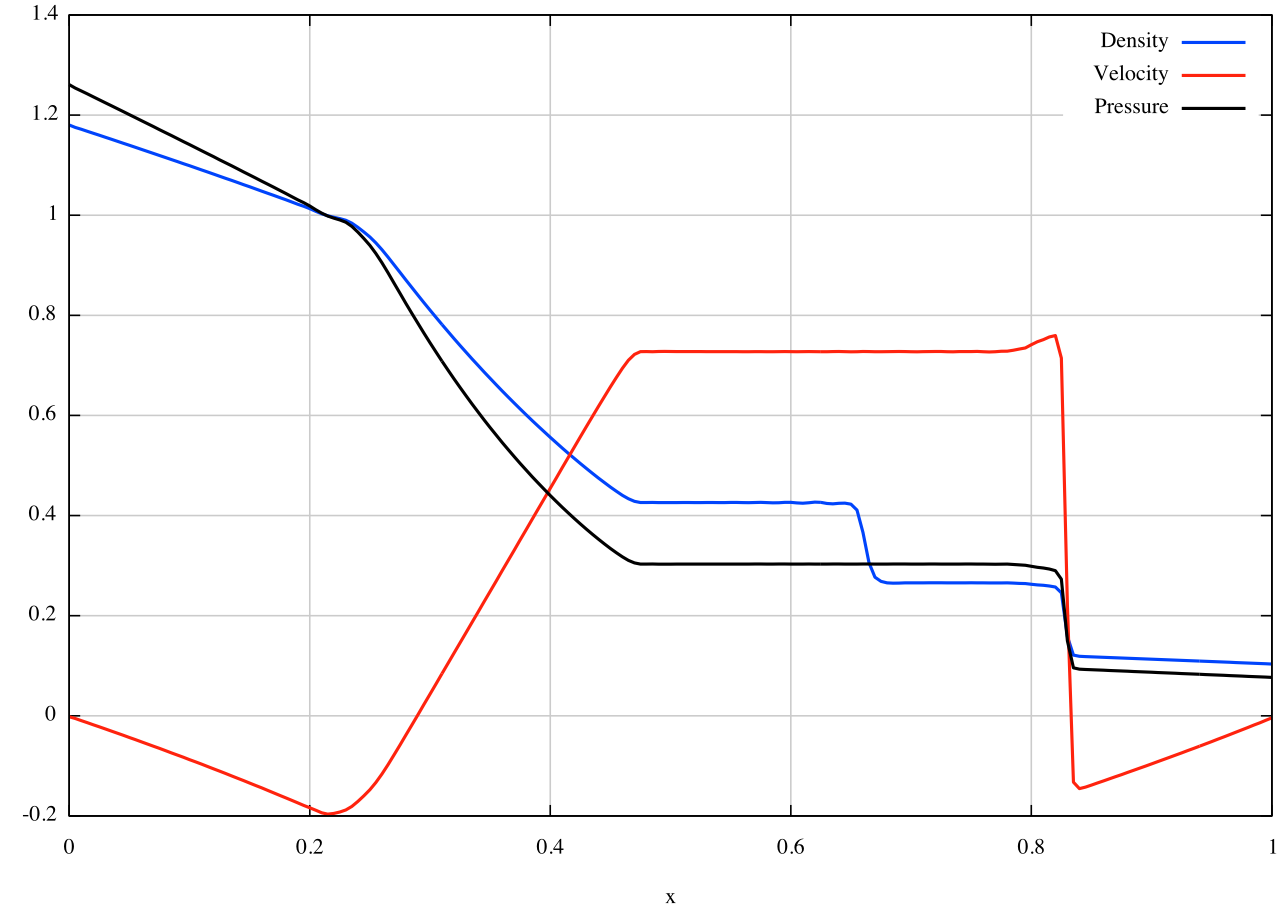
Final solution at t=0.2: The following figure is obtained by plotting op_00001.dat. Note that the output is in terms of the conserved variables, so they have to converted to the primitive variables (density, velocity, and pressure).
Expected screen output:
HyPar - Parallel (MPI) version with 1 processes
Compiled with PETSc time integration.
Reading solver inputs from file "solver.inp".
No. of dimensions : 1
No. of variables : 3
Domain size : 201
Processes along each dimension : 1
No. of ghosts pts : 3
No. of iter. : 200
Restart iteration : 0
Time integration scheme : rk (44)
Spatial discretization scheme (hyperbolic) : crweno5
Split hyperbolic flux term? : no
Interpolation type for hyperbolic term : characteristic
Spatial discretization type (parabolic ) : nonconservative-1stage
Spatial discretization scheme (parabolic ) : 2
Time Step : 1.000000E-03
Check for conservation : no
Screen output iterations : 10
File output iterations : 9999
Initial solution file type : ascii
Initial solution read mode : serial
Solution file write mode : serial
Solution file format : text
Overwrite solution file : no
Physical model : euler1d
Partitioning domain.
Allocating data arrays.
Reading array from ASCII file initial.inp (Serial mode).
Volume integral of the initial solution:
0: 5.6312499999999899E-01
1: 0.0000000000000000E+00
2: 1.3762499999999946E+00
Reading boundary conditions from "boundary.inp".
Boundary slip-wall: Along dimension 0 and face +1
Boundary slip-wall: Along dimension 0 and face -1
2 boundary condition(s) read.
Initializing solvers.
Reading WENO parameters from weno.inp.
Initializing physics. Model = "euler1d"
Reading physical model inputs from file "physics.inp".
Setting up time integration.
Solving in time (from 0 to 200 iterations)
Writing solution file op_00000.dat.
Iteration: 10 Time: 1.000E-02 Max CFL: 4.200E-01 Max Diff. No.: -1.000E+00 Norm: 1.7519E-02
Iteration: 20 Time: 2.000E-02 Max CFL: 4.316E-01 Max Diff. No.: -1.000E+00 Norm: 1.4521E-02
Iteration: 30 Time: 3.000E-02 Max CFL: 4.311E-01 Max Diff. No.: -1.000E+00 Norm: 1.4968E-02
Iteration: 40 Time: 4.000E-02 Max CFL: 4.299E-01 Max Diff. No.: -1.000E+00 Norm: 1.3338E-02
Iteration: 50 Time: 5.000E-02 Max CFL: 4.287E-01 Max Diff. No.: -1.000E+00 Norm: 1.3206E-02
Iteration: 60 Time: 6.000E-02 Max CFL: 4.270E-01 Max Diff. No.: -1.000E+00 Norm: 1.3436E-02
Iteration: 70 Time: 7.000E-02 Max CFL: 4.250E-01 Max Diff. No.: -1.000E+00 Norm: 1.2109E-02
Iteration: 80 Time: 8.000E-02 Max CFL: 4.229E-01 Max Diff. No.: -1.000E+00 Norm: 1.3268E-02
Iteration: 90 Time: 9.000E-02 Max CFL: 4.207E-01 Max Diff. No.: -1.000E+00 Norm: 1.2785E-02
Iteration: 100 Time: 1.000E-01 Max CFL: 4.188E-01 Max Diff. No.: -1.000E+00 Norm: 1.1673E-02
Iteration: 110 Time: 1.100E-01 Max CFL: 4.168E-01 Max Diff. No.: -1.000E+00 Norm: 1.2438E-02
Iteration: 120 Time: 1.200E-01 Max CFL: 4.148E-01 Max Diff. No.: -1.000E+00 Norm: 1.2803E-02
Iteration: 130 Time: 1.300E-01 Max CFL: 4.129E-01 Max Diff. No.: -1.000E+00 Norm: 1.1765E-02
Iteration: 140 Time: 1.400E-01 Max CFL: 4.107E-01 Max Diff. No.: -1.000E+00 Norm: 1.1088E-02
Iteration: 150 Time: 1.500E-01 Max CFL: 4.089E-01 Max Diff. No.: -1.000E+00 Norm: 1.1785E-02
Iteration: 160 Time: 1.600E-01 Max CFL: 4.068E-01 Max Diff. No.: -1.000E+00 Norm: 1.2485E-02
Iteration: 170 Time: 1.700E-01 Max CFL: 4.048E-01 Max Diff. No.: -1.000E+00 Norm: 1.1903E-02
Iteration: 180 Time: 1.800E-01 Max CFL: 4.028E-01 Max Diff. No.: -1.000E+00 Norm: 1.1215E-02
Iteration: 190 Time: 1.900E-01 Max CFL: 4.012E-01 Max Diff. No.: -1.000E+00 Norm: 1.0635E-02
Iteration: 200 Time: 2.000E-01 Max CFL: 4.029E-01 Max Diff. No.: -1.000E+00 Norm: 1.0358E-02
Writing solution file op_00001.dat.
Completed time integration (Final time: 0.200000).
Computed errors:
L1 Error : 0.0000000000000000E+00
L2 Error : 0.0000000000000000E+00
Linfinity Error : 0.0000000000000000E+00
Conservation Errors:
0.0000000000000000E+00
0.0000000000000000E+00
0.0000000000000000E+00
Solver runtime (in seconds): 1.2377659999999999E+00
Total runtime (in seconds): 1.2389300000000001E+00
Deallocating arrays.
Finished.