HyPar  1.0
Finite-Difference Hyperbolic-Parabolic PDE Solver on Cartesian Grids
2D Euler Equations - Radial Expansion Wave

Location: hypar/Examples/2D/NavierStokes2D/RadialExpansionWave (This directory contains all the input files needed to run this case. If there is a Run.m, run it in MATLAB to quickly set up, run, and visualize the example).

Governing equations: 2D Euler Equations (navierstokes2d.h - By default, NavierStokes2D::Re is set to -1 which makes the code skip the parabolic terms, i.e., the 2D Euler equations are solved.)

Reference: http://www.as.dlr.de/hiocfd/case_c1.5.html

Domain: \(-0.4 \le x,y \le 0.4\), "extrapolate" (_EXTRAPOLATE_) boundary conditions (supersonic outflow).

Initial solution: see reference above.

Numerical method:

Input files required:

solver.inp

begin
ndims 2
nvars 4
size 65 65
iproc 2 2
ghost 3
n_iter 100
time_scheme rk
time_scheme_type ssprk3
hyp_space_scheme weno5
hyp_interp_type characteristic
dt 0.01
screen_op_iter 1
file_op_iter 10
op_file_format tecplot2d
op_overwrite no
model navierstokes2d
end

boundary.inp

4
extrapolate 0 1 0 0 -4.0 4.0
extrapolate 0 -1 0 0 -4.0 4.0
extrapolate 1 1 -4.0 4.0 0 0
extrapolate 1 -1 -4.0 4.0 0 0

physics.inp

begin
gamma 1.4
upwinding rf-char
end

weno.inp (optional)

begin
mapped 1
borges 0
yc 0
no_limiting 0
epsilon 0.000001
p 2.0
rc 0.3
xi 0.001
end

To generate initial.inp, compile and run the following code in the run directory.

#include <stdio.h>
#include <stdlib.h>
#include <math.h>
#include <string.h>
double power(double x,double a)
{
return(exp(a*log(x)));
}
int main(){
const double pi = 4.0*atan(1.0);
const double GAMMA = 1.4;
int NI=101,NJ=101,ndims=2;
char ip_file_type[50];
strcpy(ip_file_type,"ascii");
FILE *in, *out;
printf("Reading file \"solver.inp\"...\n");
in = fopen("solver.inp","r");
if (!in) printf("Error: Input file \"solver.inp\" not found. Default values will be used.\n");
else {
char word[500];
fscanf(in,"%s",word);
if (!strcmp(word, "begin")){
while (strcmp(word, "end")){
fscanf(in,"%s",word);
if (!strcmp(word, "ndims")) fscanf(in,"%d",&ndims);
else if (!strcmp(word, "size")) {
fscanf(in,"%d",&NI);
fscanf(in,"%d",&NJ);
} else if (!strcmp(word, "ip_file_type")) fscanf(in,"%s",ip_file_type);
}
} else printf("Error: Illegal format in solver.inp. Crash and burn!\n");
}
fclose(in);
if (ndims != 2) {
printf("ndims is not 2 in solver.inp. this code is to generate 2D initial conditions\n");
return(0);
}
printf("Grid:\t\t\t%d X %d\n",NI,NJ);
int i,j;
double dx = 8.0 / ((double)(NI-1));
double dy = 8.0 / ((double)(NJ-1));
double *x, *y, *u0, *u1, *u2, *u3;
x = (double*) calloc (NI , sizeof(double));
y = (double*) calloc (NJ , sizeof(double));
u0 = (double*) calloc (NI*NJ, sizeof(double));
u1 = (double*) calloc (NI*NJ, sizeof(double));
u2 = (double*) calloc (NI*NJ, sizeof(double));
u3 = (double*) calloc (NI*NJ, sizeof(double));
for (i = 0; i < NI; i++){
for (j = 0; j < NJ; j++){
x[i] = -4.0 + i*dx;
y[j] = -4.0 + j*dy;
int p = NJ*i + j;
double r = sqrt(x[i]*x[i] + y[j]*y[j]);
double q;
if (r < 0.5) q = 0.0;
else if (r < 1.5) q = (1.0/GAMMA) * (1.0 + tanh((r-1)/(0.25-(r-1)*(r-1))));
else q = 2.0/GAMMA;
double rho, u, v, P, a;
if (r == 0) u = v = 0;
else {
u = x[i]*q/r;
v = y[j]*q/r;
}
a = 1.0 - (GAMMA-1.0)*q/2.0;
rho = GAMMA*power(a,2/(GAMMA-1.0));
P = rho*a*a/GAMMA;
u0[p] = rho;
u1[p] = rho*u;
u2[p] = rho*v;
u3[p] = P/(GAMMA-1.0) + 0.5*rho*(u*u+v*v);
}
}
if (!strcmp(ip_file_type,"ascii")) {
out = fopen("initial.inp","w");
for (i = 0; i < NI; i++) fprintf(out,"%lf ",x[i]);
fprintf(out,"\n");
for (j = 0; j < NJ; j++) fprintf(out,"%lf ",y[j]);
fprintf(out,"\n");
for (j = 0; j < NJ; j++) {
for (i = 0; i < NI; i++) {
int p = NJ*i + j;
fprintf(out,"%lf ",u0[p]);
}
}
fprintf(out,"\n");
for (j = 0; j < NJ; j++) {
for (i = 0; i < NI; i++) {
int p = NJ*i + j;
fprintf(out,"%lf ",u1[p]);
}
}
fprintf(out,"\n");
for (j = 0; j < NJ; j++) {
for (i = 0; i < NI; i++) {
int p = NJ*i + j;
fprintf(out,"%lf ",u2[p]);
}
}
fprintf(out,"\n");
for (j = 0; j < NJ; j++) {
for (i = 0; i < NI; i++) {
int p = NJ*i + j;
fprintf(out,"%lf ",u3[p]);
}
}
fprintf(out,"\n");
fclose(out);
} else if ((!strcmp(ip_file_type,"binary")) || (!strcmp(ip_file_type,"bin"))) {
printf("Error: Writing binary initial solution file not implemented. ");
printf("Please choose ip_file_type in solver.inp as \"ascii\".\n");
}
free(x);
free(y);
free(u0);
free(u1);
free(u2);
free(u3);
return(0);
}

Output:

Note that iproc is set to 

  2 2

in solver.inp (i.e., 2 processors along x, and 2 processors along y). Thus, this example should be run with 4 MPI ranks (or change iproc).

After running the code, there should be 11 output files op_00000.dat, op_00001.dat, ... op_00010.dat; the first one is the solution at \(t=0\) and the final one is the solution at \(t=1\). Since HyPar::op_overwrite is set to no in solver.inp, separate files are written for solutions at each output time.

HyPar::op_file_format is set to tecplot2d in solver.inp, and thus, all the files are in a format that Tecplot (http://www.tecplot.com/) or other visualization software supporting the Tecplot format (e.g. VisIt - https://wci.llnl.gov/simulation/computer-codes/visit/) can read. In these files, the first two lines are the Tecplot headers, after which the data is written out as: the first two columns are grid indices, the next two columns are x and y coordinates, and the remaining columns are the solution components. HyPar::op_file_format can be set to text to get the solution files in plain text format (which can be read in and visualized in MATLAB for example).

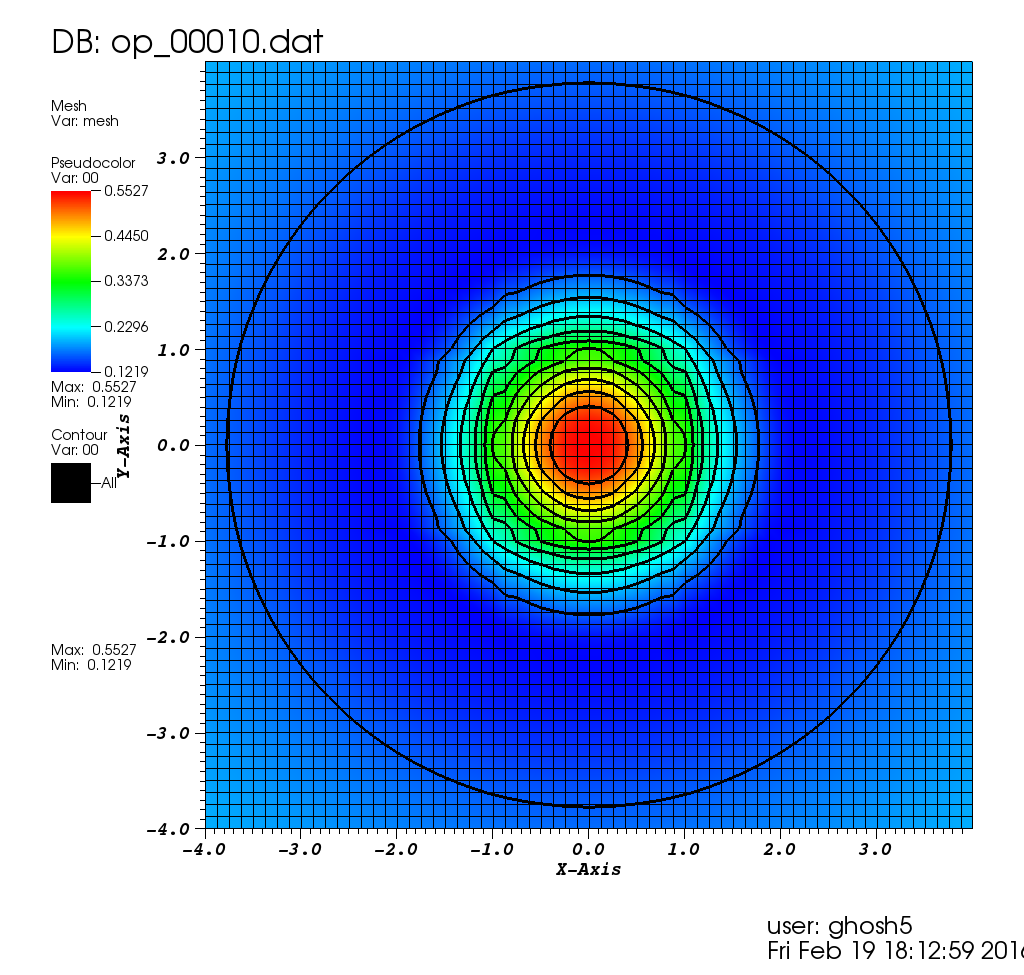
The following plot shows the density contours at the final time t=1, obtained from plotting op_00010.dat:

Solution_2DNavStokRadialExpansion.png

Expected screen output:

HyPar - Parallel (MPI) version with 4 processes
Compiled with PETSc time integration.
Reading solver inputs from file "solver.inp".
No. of dimensions : 2
No. of variables : 4
Domain size : 65 65
Processes along each dimension : 2 2
No. of ghosts pts : 3
No. of iter. : 100
Restart iteration : 0
Time integration scheme : rk (ssprk3)
Spatial discretization scheme (hyperbolic) : weno5
Split hyperbolic flux term? : no
Interpolation type for hyperbolic term : characteristic
Spatial discretization type (parabolic ) : nonconservative-1stage
Spatial discretization scheme (parabolic ) : 2
Time Step : 1.000000E-02
Check for conservation : no
Screen output iterations : 1
File output iterations : 10
Initial solution file type : ascii
Initial solution read mode : serial
Solution file write mode : serial
Solution file format : tecplot2d
Overwrite solution file : no
Physical model : navierstokes2d
Partitioning domain.
Allocating data arrays.
Reading array from ASCII file initial.inp (Serial mode).
Volume integral of the initial solution:
0: 2.0432255062500285E+01
1: 8.8817841970012523E-16
2: 1.7763568394002505E-15
3: 3.8482601062500848E+01
Reading boundary conditions from "boundary.inp".
Boundary extrapolate: Along dimension 0 and face +1
Boundary extrapolate: Along dimension 0 and face -1
Boundary extrapolate: Along dimension 1 and face +1
Boundary extrapolate: Along dimension 1 and face -1
4 boundary condition(s) read.
Initializing solvers.
Warning: File weno.inp not found. Using default parameters for WENO5/CRWENO5/HCWENO5 scheme.
Initializing physics. Model = "navierstokes2d"
Reading physical model inputs from file "physics.inp".
Setting up time integration.
Solving in time (from 0 to 100 iterations)
Writing solution file op_00000.dat.
Iteration: 1 Time: 1.000E-02 Max CFL: 1.714E-01 Max Diff. No.: -1.000E+00 Norm: 7.5863E-03
Iteration: 2 Time: 2.000E-02 Max CFL: 1.714E-01 Max Diff. No.: -1.000E+00 Norm: 7.4698E-03
Iteration: 3 Time: 3.000E-02 Max CFL: 1.713E-01 Max Diff. No.: -1.000E+00 Norm: 7.3598E-03
Iteration: 4 Time: 4.000E-02 Max CFL: 1.713E-01 Max Diff. No.: -1.000E+00 Norm: 7.2576E-03
Iteration: 5 Time: 5.000E-02 Max CFL: 1.713E-01 Max Diff. No.: -1.000E+00 Norm: 7.1639E-03
Iteration: 6 Time: 6.000E-02 Max CFL: 1.712E-01 Max Diff. No.: -1.000E+00 Norm: 7.0781E-03
Iteration: 7 Time: 7.000E-02 Max CFL: 1.712E-01 Max Diff. No.: -1.000E+00 Norm: 6.9990E-03
Iteration: 8 Time: 8.000E-02 Max CFL: 1.711E-01 Max Diff. No.: -1.000E+00 Norm: 6.9256E-03
Iteration: 9 Time: 9.000E-02 Max CFL: 1.711E-01 Max Diff. No.: -1.000E+00 Norm: 6.8574E-03
Iteration: 10 Time: 1.000E-01 Max CFL: 1.710E-01 Max Diff. No.: -1.000E+00 Norm: 6.7924E-03
Writing solution file op_00001.dat.
Iteration: 11 Time: 1.100E-01 Max CFL: 1.710E-01 Max Diff. No.: -1.000E+00 Norm: 6.7287E-03
Iteration: 12 Time: 1.200E-01 Max CFL: 1.710E-01 Max Diff. No.: -1.000E+00 Norm: 6.6650E-03
Iteration: 13 Time: 1.300E-01 Max CFL: 1.709E-01 Max Diff. No.: -1.000E+00 Norm: 6.6022E-03
Iteration: 14 Time: 1.400E-01 Max CFL: 1.709E-01 Max Diff. No.: -1.000E+00 Norm: 6.5416E-03
Iteration: 15 Time: 1.500E-01 Max CFL: 1.708E-01 Max Diff. No.: -1.000E+00 Norm: 6.4845E-03
Iteration: 16 Time: 1.600E-01 Max CFL: 1.708E-01 Max Diff. No.: -1.000E+00 Norm: 6.4309E-03
Iteration: 17 Time: 1.700E-01 Max CFL: 1.707E-01 Max Diff. No.: -1.000E+00 Norm: 6.3806E-03
Iteration: 18 Time: 1.800E-01 Max CFL: 1.707E-01 Max Diff. No.: -1.000E+00 Norm: 6.3327E-03
Iteration: 19 Time: 1.900E-01 Max CFL: 1.706E-01 Max Diff. No.: -1.000E+00 Norm: 6.2867E-03
Iteration: 20 Time: 2.000E-01 Max CFL: 1.706E-01 Max Diff. No.: -1.000E+00 Norm: 6.2420E-03
Writing solution file op_00002.dat.
Iteration: 21 Time: 2.100E-01 Max CFL: 1.705E-01 Max Diff. No.: -1.000E+00 Norm: 6.1982E-03
Iteration: 22 Time: 2.200E-01 Max CFL: 1.705E-01 Max Diff. No.: -1.000E+00 Norm: 6.1552E-03
Iteration: 23 Time: 2.300E-01 Max CFL: 1.704E-01 Max Diff. No.: -1.000E+00 Norm: 6.1128E-03
Iteration: 24 Time: 2.400E-01 Max CFL: 1.704E-01 Max Diff. No.: -1.000E+00 Norm: 6.0714E-03
Iteration: 25 Time: 2.500E-01 Max CFL: 1.703E-01 Max Diff. No.: -1.000E+00 Norm: 6.0310E-03
Iteration: 26 Time: 2.600E-01 Max CFL: 1.703E-01 Max Diff. No.: -1.000E+00 Norm: 5.9919E-03
Iteration: 27 Time: 2.700E-01 Max CFL: 1.702E-01 Max Diff. No.: -1.000E+00 Norm: 5.9539E-03
Iteration: 28 Time: 2.800E-01 Max CFL: 1.701E-01 Max Diff. No.: -1.000E+00 Norm: 5.9169E-03
Iteration: 29 Time: 2.900E-01 Max CFL: 1.701E-01 Max Diff. No.: -1.000E+00 Norm: 5.8808E-03
Iteration: 30 Time: 3.000E-01 Max CFL: 1.700E-01 Max Diff. No.: -1.000E+00 Norm: 5.8457E-03
Writing solution file op_00003.dat.
Iteration: 31 Time: 3.100E-01 Max CFL: 1.700E-01 Max Diff. No.: -1.000E+00 Norm: 5.8115E-03
Iteration: 32 Time: 3.200E-01 Max CFL: 1.699E-01 Max Diff. No.: -1.000E+00 Norm: 5.7783E-03
Iteration: 33 Time: 3.300E-01 Max CFL: 1.699E-01 Max Diff. No.: -1.000E+00 Norm: 5.7457E-03
Iteration: 34 Time: 3.400E-01 Max CFL: 1.698E-01 Max Diff. No.: -1.000E+00 Norm: 5.7136E-03
Iteration: 35 Time: 3.500E-01 Max CFL: 1.697E-01 Max Diff. No.: -1.000E+00 Norm: 5.6819E-03
Iteration: 36 Time: 3.600E-01 Max CFL: 1.697E-01 Max Diff. No.: -1.000E+00 Norm: 5.6507E-03
Iteration: 37 Time: 3.700E-01 Max CFL: 1.696E-01 Max Diff. No.: -1.000E+00 Norm: 5.6198E-03
Iteration: 38 Time: 3.800E-01 Max CFL: 1.696E-01 Max Diff. No.: -1.000E+00 Norm: 5.5895E-03
Iteration: 39 Time: 3.900E-01 Max CFL: 1.695E-01 Max Diff. No.: -1.000E+00 Norm: 5.5599E-03
Iteration: 40 Time: 4.000E-01 Max CFL: 1.694E-01 Max Diff. No.: -1.000E+00 Norm: 5.5311E-03
Writing solution file op_00004.dat.
Iteration: 41 Time: 4.100E-01 Max CFL: 1.694E-01 Max Diff. No.: -1.000E+00 Norm: 5.5033E-03
Iteration: 42 Time: 4.200E-01 Max CFL: 1.693E-01 Max Diff. No.: -1.000E+00 Norm: 5.4762E-03
Iteration: 43 Time: 4.300E-01 Max CFL: 1.692E-01 Max Diff. No.: -1.000E+00 Norm: 5.4497E-03
Iteration: 44 Time: 4.400E-01 Max CFL: 1.692E-01 Max Diff. No.: -1.000E+00 Norm: 5.4236E-03
Iteration: 45 Time: 4.500E-01 Max CFL: 1.691E-01 Max Diff. No.: -1.000E+00 Norm: 5.3979E-03
Iteration: 46 Time: 4.600E-01 Max CFL: 1.690E-01 Max Diff. No.: -1.000E+00 Norm: 5.3727E-03
Iteration: 47 Time: 4.700E-01 Max CFL: 1.690E-01 Max Diff. No.: -1.000E+00 Norm: 5.3480E-03
Iteration: 48 Time: 4.800E-01 Max CFL: 1.689E-01 Max Diff. No.: -1.000E+00 Norm: 5.3239E-03
Iteration: 49 Time: 4.900E-01 Max CFL: 1.688E-01 Max Diff. No.: -1.000E+00 Norm: 5.3004E-03
Iteration: 50 Time: 5.000E-01 Max CFL: 1.688E-01 Max Diff. No.: -1.000E+00 Norm: 5.2777E-03
Writing solution file op_00005.dat.
Iteration: 51 Time: 5.100E-01 Max CFL: 1.687E-01 Max Diff. No.: -1.000E+00 Norm: 5.2558E-03
Iteration: 52 Time: 5.200E-01 Max CFL: 1.686E-01 Max Diff. No.: -1.000E+00 Norm: 5.2346E-03
Iteration: 53 Time: 5.300E-01 Max CFL: 1.685E-01 Max Diff. No.: -1.000E+00 Norm: 5.2142E-03
Iteration: 54 Time: 5.400E-01 Max CFL: 1.685E-01 Max Diff. No.: -1.000E+00 Norm: 5.1945E-03
Iteration: 55 Time: 5.500E-01 Max CFL: 1.684E-01 Max Diff. No.: -1.000E+00 Norm: 5.1755E-03
Iteration: 56 Time: 5.600E-01 Max CFL: 1.683E-01 Max Diff. No.: -1.000E+00 Norm: 5.1570E-03
Iteration: 57 Time: 5.700E-01 Max CFL: 1.682E-01 Max Diff. No.: -1.000E+00 Norm: 5.1390E-03
Iteration: 58 Time: 5.800E-01 Max CFL: 1.682E-01 Max Diff. No.: -1.000E+00 Norm: 5.1216E-03
Iteration: 59 Time: 5.900E-01 Max CFL: 1.681E-01 Max Diff. No.: -1.000E+00 Norm: 5.1047E-03
Iteration: 60 Time: 6.000E-01 Max CFL: 1.680E-01 Max Diff. No.: -1.000E+00 Norm: 5.0883E-03
Writing solution file op_00006.dat.
Iteration: 61 Time: 6.100E-01 Max CFL: 1.679E-01 Max Diff. No.: -1.000E+00 Norm: 5.0723E-03
Iteration: 62 Time: 6.200E-01 Max CFL: 1.678E-01 Max Diff. No.: -1.000E+00 Norm: 5.0567E-03
Iteration: 63 Time: 6.300E-01 Max CFL: 1.678E-01 Max Diff. No.: -1.000E+00 Norm: 5.0412E-03
Iteration: 64 Time: 6.400E-01 Max CFL: 1.677E-01 Max Diff. No.: -1.000E+00 Norm: 5.0259E-03
Iteration: 65 Time: 6.500E-01 Max CFL: 1.676E-01 Max Diff. No.: -1.000E+00 Norm: 5.0104E-03
Iteration: 66 Time: 6.600E-01 Max CFL: 1.675E-01 Max Diff. No.: -1.000E+00 Norm: 4.9945E-03
Iteration: 67 Time: 6.700E-01 Max CFL: 1.674E-01 Max Diff. No.: -1.000E+00 Norm: 4.9782E-03
Iteration: 68 Time: 6.800E-01 Max CFL: 1.673E-01 Max Diff. No.: -1.000E+00 Norm: 4.9612E-03
Iteration: 69 Time: 6.900E-01 Max CFL: 1.672E-01 Max Diff. No.: -1.000E+00 Norm: 4.9434E-03
Iteration: 70 Time: 7.000E-01 Max CFL: 1.671E-01 Max Diff. No.: -1.000E+00 Norm: 4.9247E-03
Writing solution file op_00007.dat.
Iteration: 71 Time: 7.100E-01 Max CFL: 1.671E-01 Max Diff. No.: -1.000E+00 Norm: 4.9051E-03
Iteration: 72 Time: 7.200E-01 Max CFL: 1.670E-01 Max Diff. No.: -1.000E+00 Norm: 4.8844E-03
Iteration: 73 Time: 7.300E-01 Max CFL: 1.669E-01 Max Diff. No.: -1.000E+00 Norm: 4.8627E-03
Iteration: 74 Time: 7.400E-01 Max CFL: 1.668E-01 Max Diff. No.: -1.000E+00 Norm: 4.8398E-03
Iteration: 75 Time: 7.500E-01 Max CFL: 1.667E-01 Max Diff. No.: -1.000E+00 Norm: 4.8155E-03
Iteration: 76 Time: 7.600E-01 Max CFL: 1.666E-01 Max Diff. No.: -1.000E+00 Norm: 4.7899E-03
Iteration: 77 Time: 7.700E-01 Max CFL: 1.665E-01 Max Diff. No.: -1.000E+00 Norm: 4.7628E-03
Iteration: 78 Time: 7.800E-01 Max CFL: 1.664E-01 Max Diff. No.: -1.000E+00 Norm: 4.7342E-03
Iteration: 79 Time: 7.900E-01 Max CFL: 1.663E-01 Max Diff. No.: -1.000E+00 Norm: 4.7042E-03
Iteration: 80 Time: 8.000E-01 Max CFL: 1.662E-01 Max Diff. No.: -1.000E+00 Norm: 4.6729E-03
Writing solution file op_00008.dat.
Iteration: 81 Time: 8.100E-01 Max CFL: 1.661E-01 Max Diff. No.: -1.000E+00 Norm: 4.6406E-03
Iteration: 82 Time: 8.200E-01 Max CFL: 1.660E-01 Max Diff. No.: -1.000E+00 Norm: 4.6072E-03
Iteration: 83 Time: 8.300E-01 Max CFL: 1.659E-01 Max Diff. No.: -1.000E+00 Norm: 4.5729E-03
Iteration: 84 Time: 8.400E-01 Max CFL: 1.658E-01 Max Diff. No.: -1.000E+00 Norm: 4.5378E-03
Iteration: 85 Time: 8.500E-01 Max CFL: 1.657E-01 Max Diff. No.: -1.000E+00 Norm: 4.5019E-03
Iteration: 86 Time: 8.600E-01 Max CFL: 1.656E-01 Max Diff. No.: -1.000E+00 Norm: 4.4653E-03
Iteration: 87 Time: 8.700E-01 Max CFL: 1.654E-01 Max Diff. No.: -1.000E+00 Norm: 4.4281E-03
Iteration: 88 Time: 8.800E-01 Max CFL: 1.653E-01 Max Diff. No.: -1.000E+00 Norm: 4.3903E-03
Iteration: 89 Time: 8.900E-01 Max CFL: 1.652E-01 Max Diff. No.: -1.000E+00 Norm: 4.3521E-03
Iteration: 90 Time: 9.000E-01 Max CFL: 1.651E-01 Max Diff. No.: -1.000E+00 Norm: 4.3135E-03
Writing solution file op_00009.dat.
Iteration: 91 Time: 9.100E-01 Max CFL: 1.651E-01 Max Diff. No.: -1.000E+00 Norm: 4.2747E-03
Iteration: 92 Time: 9.200E-01 Max CFL: 1.650E-01 Max Diff. No.: -1.000E+00 Norm: 4.2357E-03
Iteration: 93 Time: 9.300E-01 Max CFL: 1.650E-01 Max Diff. No.: -1.000E+00 Norm: 4.1966E-03
Iteration: 94 Time: 9.400E-01 Max CFL: 1.649E-01 Max Diff. No.: -1.000E+00 Norm: 4.1575E-03
Iteration: 95 Time: 9.500E-01 Max CFL: 1.649E-01 Max Diff. No.: -1.000E+00 Norm: 4.1184E-03
Iteration: 96 Time: 9.600E-01 Max CFL: 1.650E-01 Max Diff. No.: -1.000E+00 Norm: 4.0793E-03
Iteration: 97 Time: 9.700E-01 Max CFL: 1.650E-01 Max Diff. No.: -1.000E+00 Norm: 4.0404E-03
Iteration: 98 Time: 9.800E-01 Max CFL: 1.650E-01 Max Diff. No.: -1.000E+00 Norm: 4.0016E-03
Iteration: 99 Time: 9.900E-01 Max CFL: 1.650E-01 Max Diff. No.: -1.000E+00 Norm: 3.9630E-03
Iteration: 100 Time: 1.000E+00 Max CFL: 1.650E-01 Max Diff. No.: -1.000E+00 Norm: 3.9246E-03
Writing solution file op_00010.dat.
Completed time integration (Final time: 1.000000).
Computed errors:
L1 Error : 0.0000000000000000E+00
L2 Error : 0.0000000000000000E+00
Linfinity Error : 0.0000000000000000E+00
Conservation Errors:
0.0000000000000000E+00
0.0000000000000000E+00
0.0000000000000000E+00
0.0000000000000000E+00
Solver runtime (in seconds): 2.7592850000000002E+00
Total runtime (in seconds): 2.7687179999999998E+00
Deallocating arrays.
Finished.