2D Shallow Water Equations - Circular Dam Break
Location: hypar/Examples/2D/ShallowWater2D/CircularDamBreak (This directory contains all the input files needed to run this case. If there is a Run.m, run it in MATLAB to quickly set up, run, and visualize the example).
Governing equations: 2D Shallow Water Equations (shallowwater2d.h)
References:
- Delis, Katsaounis, "Numerical solution of the two-dimensional shallow water equations by the application of relaxation methods", Applied Mathematical Modelling, 29 (2005), pp. 754-783 (Section 6.3).
Domain: \(0 \le x,y \le 50 \), "extrapolate" (_EXTRAPOLATE_) boundary conditions everywhere
Initial solution:
\begin{equation} h\left(x,y\right) = \left\{\begin{array}{cc}10 & r \le 11.0\\1 & {\rm otherwise}\end{array}\right., u\left(x,y\right) = 0. \end{equation}
with the bottom topography as \(b\left(x,y\right) = 0\), and \(r^2=\left(x-25\right)^2+\left(y-25\right)^2\).
Other parameters:
- \(g=9.8\) (ShallowWater2D::g)
Numerical Method:
- Spatial discretization (hyperbolic): 5th order WENO (Interp1PrimFifthOrderWENO())
- Time integration: RK4 (TimeRK(), _RK_44_)
Input files required:
Note: in addition to the usual input files that HyPar needs, this physical model needs the following input file(s):
- topography.inp : file containing the bottom topography (same format as initial.inp).
However, this case has a constant (zero) bottom topography, and thus this file can be skipped.
solver.inp
begin
ndims 2
nvars 3
size 101 101
iproc 2 2
ghost 3
n_iter 23
restart_iter 0
time_scheme rk
time_scheme_type 44
hyp_space_scheme weno5
hyp_interp_type components
dt 0.03
conservation_check no
screen_op_iter 1
file_op_iter 5
op_file_format text
ip_file_type ascii
input_mode serial
output_mode serial
op_overwrite no
model shallow-water-2d
end
boundary.inp
4
extrapolate 0 1 0 0 0 50.0
extrapolate 0 -1 0 0 0 50.0
extrapolate 1 1 0 50.0 0 0
extrapolate 1 -1 0 50.0 0 0
physics.inp
begin
gravity 9.8
topography_type 0
upwinding llf-char
end
weno.inp (optional)
begin
mapped 0
borges 0
yc 1
no_limiting 0
epsilon 1.0e-6
p 2
rc 0.3
xi 0.001
tol 1e-16
end
To generate initial.inp and topography.inp, compile and run the following code in the run directory (note: topography.inp can be skipped since this case involves a uniform topography).
/*
Code to generate the initial solution for:
Case: Small Peturbation
Model: ShallowWater2D
Reference:
Delis, Katsaounis, "Numerical solution of the two-dimensional
shallow water equations by the application of relaxation methods",
Applied Mathematical Modelling, 29 (2005), pp. 754--783
http://dx.doi.org/10.1016/j.apm.2004.11.001
Section 6.3
Needs: solver.inp
Writes out: initial.inp, topography.inp
*/
#include <stdio.h>
#include <stdlib.h>
#include <math.h>
#include <string.h>
int main(){
int NI = 101, NJ = 101, ndims = 2;
char ip_file_type[50];
strcpy(ip_file_type,"ascii");
FILE *in;
printf("Reading file \"solver.inp\"...\n");
in = fopen("solver.inp","r");
if (!in) {
printf("Error: Input file \"solver.inp\" not found.\n");
return(0);
} else {
char word[500];
fscanf(in,"%s",word);
if (!strcmp(word, "begin")) {
while (strcmp(word, "end")) {
fscanf(in,"%s",word);
if (!strcmp(word, "ndims")) fscanf(in,"%d",&ndims);
else if (!strcmp(word, "size")) {
fscanf(in,"%d",&NI);
fscanf(in,"%d",&NJ);
} else if (!strcmp(word, "ip_file_type")) fscanf(in,"%s",ip_file_type);
}
} else printf("Error: Illegal format in solver.inp. Crash and burn!\n");
}
fclose(in);
if (ndims != 2) {
printf("ndims is not 2 in solver.inp. this code is to generate 2D initial conditions\n");
return(0);
}
printf("Grid:\t\t\t%d X %d\n",NI,NJ);
int i,j;
double length_x = 50.0, length_y = 50.0;
double dx = length_x / ((double)NI-1);
double dy = length_y / ((double)NJ-1);
double *x, *y, *u0, *u1, *u2, *b;
x = (double*) calloc (NI , sizeof(double));
y = (double*) calloc (NJ , sizeof(double));
u0 = (double*) calloc (NI*NJ, sizeof(double));
u1 = (double*) calloc (NI*NJ, sizeof(double));
u2 = (double*) calloc (NI*NJ, sizeof(double));
b = (double*) calloc (NI*NJ, sizeof(double));
for (i = 0; i < NI; i++){
for (j = 0; j < NJ; j++){
x[i] = i*dx;
y[j] = j*dy;
double r = sqrt((x[i]-length_x/2)*(x[i]-length_x/2)+(y[j]-length_y/2)*(y[j]-length_y/2));
int p = NI*j + i;
double h, u, v;
b[p] = 0.0;
if (r <= 11.0) h = 10.0;
else h = 1.0;
u = v = 0.0;
u0[p] = h;
u1[p] = h*u;
u2[p] = h*v;
}
}
FILE *out;
if (!strcmp(ip_file_type,"ascii")) {
printf("Writing ASCII initial solution file initial.inp\n");
out = fopen("initial.inp","w");
for (i = 0; i < NI; i++) fprintf(out,"%1.16e ",x[i]);
fprintf(out,"\n");
for (j = 0; j < NJ; j++) fprintf(out,"%1.16e ",y[j]);
fprintf(out,"\n");
for (j = 0; j < NJ; j++) {
for (i = 0; i < NI; i++) {
int p = NI*j + i;
fprintf(out,"%1.16e ",u0[p]);
}
}
fprintf(out,"\n");
for (j = 0; j < NJ; j++) {
for (i = 0; i < NI; i++) {
int p = NI*j + i;
fprintf(out,"%1.16e ",u1[p]);
}
}
fprintf(out,"\n");
for (j = 0; j < NJ; j++) {
for (i = 0; i < NI; i++) {
int p = NI*j + i;
fprintf(out,"%1.16e ",u2[p]);
}
}
fprintf(out,"\n");
fclose(out);
printf("Writing ASCII topography file topography.inp\n");
out = fopen("topography.inp","w");
for (i = 0; i < NI; i++) fprintf(out,"%1.16e ",x[i]);
fprintf(out,"\n");
for (j = 0; j < NJ; j++) fprintf(out,"%1.16e ",y[j]);
fprintf(out,"\n");
for (j = 0; j < NJ; j++) {
for (i = 0; i < NI; i++) {
int p = NI*j + i;
fprintf(out,"%1.16e ",b[p]);
}
}
fprintf(out,"\n");
fclose(out);
} else if ((!strcmp(ip_file_type,"binary")) || (!strcmp(ip_file_type,"bin"))) {
printf("Writing binary initial solution file initial.inp\n");
out = fopen("initial.inp","wb");
fwrite(x,sizeof(double),NI,out);
fwrite(y,sizeof(double),NJ,out);
double *U = (double*) calloc (3*NI*NJ,sizeof(double));
for (i=0; i < NI; i++) {
for (j = 0; j < NJ; j++) {
int p = NI*j + i;
U[3*p+0] = u0[p];
U[3*p+1] = u1[p];
U[3*p+2] = u2[p];
}
}
fwrite(U,sizeof(double),3*NI*NJ,out);
free(U);
fclose(out);
printf("Writing binary topography file topography.inp\n");
out = fopen("topography.inp","wb");
fwrite(x,sizeof(double),NI,out);
fwrite(y,sizeof(double),NJ,out);
fwrite(b,sizeof(double),NI*NJ,out);
fclose(out);
}
free(x);
free(y);
free(u0);
free(u1);
free(u2);
free(b);
return(0);
}
Output:
Note that iproc is set to
2 2
in solver.inp (i.e., 2 processors along x, and 2 processors along y). Thus, this example should be run with 4 MPI ranks (or change iproc).
After running the code, there should be 6 solution output files op_00000.dat, ..., op_00005.dat; the first one is the solution at \(t=0\) and the final one is the solution at \(t=0.69\). Since HyPar::op_overwrite is set to no in solver.inp, separate files are written for solutions at each output time.
HyPar::op_file_format is set to text in solver.inp, and thus, all the files are in plain text (ASCII) format. In these files, the data is written out as: the first two columns are grid indices, the next two columns are the x and y coordinates, and the remaining columns are the three solution components. HyPar::op_file_format can also be set to tecplot2d to get the solution files in the Tecplot format (that can be read using any visualization software that supports Tecplot format).
In addition to the usual output files, the shallow water physics module writes out the following files:
- topography_00000.dat, ..., topography_00005.dat: These files share the same format as the solution output files op_*.dat and contains the topography \(b\left(x\right)\) (for this example, they do not matter since the topography is flat).
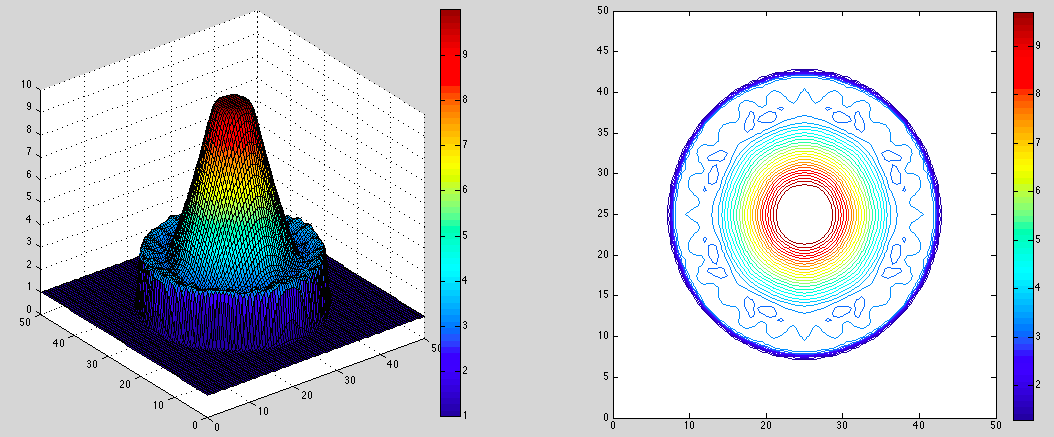
The following plot shows the final solution (water height):
It was obtained by using the following MATLAB code to plot op_00005.dat:
clear all;
close all;
fname = input('Enter name of file to plot: ','s');
% Load topography file
topo = load('topography_00000.dat');
% find out max grid sizes
imax = max(topo(:,1)) + 1;
jmax = max(topo(:,2)) + 1;
%spatial coordinates
xcoord = reshape(topo(:,3),imax,jmax);
ycoord = reshape(topo(:,4),imax,jmax);
% bottom topography
b = reshape(topo(:,5),imax,jmax);
% figure(1);
% surf(xcoord,ycoord,b);
% hold on;
% read solution
data = load(fname);
h = reshape(data(:,5),imax,jmax);
u = reshape(data(:,6),imax,jmax)./h;
v = reshape(data(:,7),imax,jmax)./h;
% plot
figure(1);
set(1, 'Position', [100, 100, 1300, 500]);
subplot(1,2,1);
surf(xcoord,ycoord,h+b);
colorbar;
subplot(1,2,2);
contour(xcoord,ycoord,h+b,30);
colorbar;
% figure(3);
% quiver(xcoord,ycoord,u,v);
Expected screen output:
HyPar - Parallel (MPI) version with 4 processes
Compiled with PETSc time integration.
Reading solver inputs from file "solver.inp".
No. of dimensions : 2
No. of variables : 3
Domain size : 101 101
Processes along each dimension : 2 2
No. of ghosts pts : 3
No. of iter. : 23
Restart iteration : 0
Time integration scheme : rk (44)
Spatial discretization scheme (hyperbolic) : weno5
Split hyperbolic flux term? : no
Interpolation type for hyperbolic term : components
Spatial discretization type (parabolic ) : nonconservative-1stage
Spatial discretization scheme (parabolic ) : 2
Time Step : 3.000000E-02
Check for conservation : no
Screen output iterations : 1
File output iterations : 5
Initial solution file type : ascii
Initial solution read mode : serial
Solution file write mode : serial
Solution file format : text
Overwrite solution file : no
Physical model : shallow-water-2d
Partitioning domain.
Allocating data arrays.
Reading array from ASCII file initial.inp (Serial mode).
Volume integral of the initial solution:
0: 5.9635000000000000E+03
1: 0.0000000000000000E+00
2: 0.0000000000000000E+00
Reading boundary conditions from "boundary.inp".
Boundary extrapolate: Along dimension 0 and face +1
Boundary extrapolate: Along dimension 0 and face -1
Boundary extrapolate: Along dimension 1 and face +1
Boundary extrapolate: Along dimension 1 and face -1
4 boundary condition(s) read.
Initializing solvers.
Reading WENO parameters from weno.inp.
Initializing physics. Model = "shallow-water-2d"
Reading physical model inputs from file "physics.inp".
Reading array from ASCII file topography.inp (Serial mode).
Setting up time integration.
Solving in time (from 0 to 23 iterations)
Writing solution file topography_00000.dat.
Writing solution file op_00000.dat.
Iteration: 1 Time: 3.000E-02 Max CFL: 5.940E-01 Max Diff. No.: -1.000E+00 Norm: 2.1446E+00
Iteration: 2 Time: 6.000E-02 Max CFL: 6.389E-01 Max Diff. No.: -1.000E+00 Norm: 1.7198E+00
Iteration: 3 Time: 9.000E-02 Max CFL: 7.394E-01 Max Diff. No.: -1.000E+00 Norm: 1.5788E+00
Iteration: 4 Time: 1.200E-01 Max CFL: 7.938E-01 Max Diff. No.: -1.000E+00 Norm: 1.5427E+00
Iteration: 5 Time: 1.500E-01 Max CFL: 8.090E-01 Max Diff. No.: -1.000E+00 Norm: 1.5990E+00
Writing solution file topography_00001.dat.
Writing solution file op_00001.dat.
Iteration: 6 Time: 1.800E-01 Max CFL: 8.141E-01 Max Diff. No.: -1.000E+00 Norm: 1.5904E+00
Iteration: 7 Time: 2.100E-01 Max CFL: 8.198E-01 Max Diff. No.: -1.000E+00 Norm: 1.5987E+00
Iteration: 8 Time: 2.400E-01 Max CFL: 8.230E-01 Max Diff. No.: -1.000E+00 Norm: 1.5495E+00
Iteration: 9 Time: 2.700E-01 Max CFL: 8.136E-01 Max Diff. No.: -1.000E+00 Norm: 1.5005E+00
Iteration: 10 Time: 3.000E-01 Max CFL: 8.088E-01 Max Diff. No.: -1.000E+00 Norm: 1.4895E+00
Writing solution file topography_00002.dat.
Writing solution file op_00002.dat.
Iteration: 11 Time: 3.300E-01 Max CFL: 8.005E-01 Max Diff. No.: -1.000E+00 Norm: 1.4770E+00
Iteration: 12 Time: 3.600E-01 Max CFL: 7.994E-01 Max Diff. No.: -1.000E+00 Norm: 1.4448E+00
Iteration: 13 Time: 3.900E-01 Max CFL: 7.997E-01 Max Diff. No.: -1.000E+00 Norm: 1.4009E+00
Iteration: 14 Time: 4.200E-01 Max CFL: 7.996E-01 Max Diff. No.: -1.000E+00 Norm: 1.3804E+00
Iteration: 15 Time: 4.500E-01 Max CFL: 7.983E-01 Max Diff. No.: -1.000E+00 Norm: 1.3847E+00
Writing solution file topography_00003.dat.
Writing solution file op_00003.dat.
Iteration: 16 Time: 4.800E-01 Max CFL: 7.975E-01 Max Diff. No.: -1.000E+00 Norm: 1.3753E+00
Iteration: 17 Time: 5.100E-01 Max CFL: 7.996E-01 Max Diff. No.: -1.000E+00 Norm: 1.3552E+00
Iteration: 18 Time: 5.400E-01 Max CFL: 7.998E-01 Max Diff. No.: -1.000E+00 Norm: 1.3290E+00
Iteration: 19 Time: 5.700E-01 Max CFL: 7.992E-01 Max Diff. No.: -1.000E+00 Norm: 1.3346E+00
Iteration: 20 Time: 6.000E-01 Max CFL: 7.977E-01 Max Diff. No.: -1.000E+00 Norm: 1.3309E+00
Writing solution file topography_00004.dat.
Writing solution file op_00004.dat.
Iteration: 21 Time: 6.300E-01 Max CFL: 7.953E-01 Max Diff. No.: -1.000E+00 Norm: 1.3274E+00
Iteration: 22 Time: 6.600E-01 Max CFL: 7.926E-01 Max Diff. No.: -1.000E+00 Norm: 1.2948E+00
Iteration: 23 Time: 6.900E-01 Max CFL: 7.905E-01 Max Diff. No.: -1.000E+00 Norm: 1.3033E+00
Writing solution file topography_00005.dat.
Writing solution file op_00005.dat.
Completed time integration (Final time: 0.690000).
Computed errors:
L1 Error : 0.0000000000000000E+00
L2 Error : 0.0000000000000000E+00
Linfinity Error : 0.0000000000000000E+00
Conservation Errors:
0.0000000000000000E+00
0.0000000000000000E+00
0.0000000000000000E+00
Solver runtime (in seconds): 2.5471050000000002E+00
Total runtime (in seconds): 2.5777280000000000E+00
Deallocating arrays.
Finished.