3D Navier-Stokes Equations - Isotropic Turbulence Decay
Location: hypar/Examples/3D/NavierStokes3D/DNS_IsotropicTurbulenceDecay (This directory contains all the input files needed to run this case. If there is a Run.m, run it in MATLAB to quickly set up, run, and visualize the example).
Governing equations: 3D Navier-Stokes Equations (navierstokes3d.h)
Domain: \(0 \le x,y,z < 2\pi\), "periodic" (_PERIODIC_) boundaries everywhere.
Initial solution: Isotropic turbulent flow - The initial solution is specified in the Fourier space (with an energy distribution similar to that of turbulent flow), and then transformed to the physical space through an inverse transform.
Other parameters:
- \(\gamma = 1.4\) (NavierStokes3D::gamma)
- \(Re = \frac {\rho u L } {\mu} = 333.33\) (NavierStokes3D::Re)
- \(Pr = 0.72\) (Prandtl number) (NavierStokes3D::Pr)
- \(M_\infty = 0.3\) (turbulence fluctuation Mach number) (NavierStokes3D::Minf)
Numerical Method:
- Spatial discretization (hyperbolic): 5th order CRWENO (Interp1PrimFifthOrderCRWENO())
- Spatial discretization (parabolic) : 4th order (FirstDerivativeFourthOrderCentral()) non-conservative 2-stage (ParabolicFunctionNC2Stage())
- Time integration: RK4 (TimeRK(), _RK_44_)
Input files required:
solver.inp
begin
ndims 3
nvars 5
size 64 64 64
iproc 2 2 1
ghost 3
n_iter 200
restart_iter 0
time_scheme rk
time_scheme_type 44
hyp_space_scheme crweno5
hyp_interp_type components
par_space_type nonconservative-2stage
par_space_scheme 4
dt 0.025
screen_op_iter 10
file_op_iter 20
ip_file_type binary
input_mode serial
op_file_format binary
op_overwrite no
model navierstokes3d
end
boundary.inp
6
periodic 0 1 0 0 0 6.3 0 6.3
periodic 0 -1 0 0 0 6.3 0 6.3
periodic 1 1 0 6.3 0 0 0 6.3
periodic 1 -1 0 6.3 0 0 0 6.3
periodic 2 1 0 6.3 0 6.3 0 0
periodic 2 -1 0 6.3 0 6.3 0 0
physics.inp
begin
gamma 1.4
upwinding roe
Pr 0.72
Minf 0.3
Re 333.333333333333333
end
weno.inp (optional)
begin
mapped 1
borges 0
yc 0
no_limiting 0
epsilon 0.000001
p 2.0
rc 0.3
xi 0.001
end
lusolver.inp (optional)
begin
reducedsolvetype jacobi
evaluate_norm 0
maxiter 10
atol 1e-12
rtol 1e-10
verbose 0
end
To generate initial.inp (initial solution), compile and run the following code in the run directory. Note: this code requires the FFTW library installed (http://www.fftw.org/). To compile:
gcc -I/path/to/fftw3.h -L/path/to/libfftw3.a -lfftw3 init.c
(see the FFTW website on ways to install it).
/*
This code generates the initial solution for the
isotropic turbulence decay problem, using the technique
described in the 1981 NASA report by Rogallo.
It needs the FFTW3 library installed. To compile it,
make sure the fftw3.h and libfftw3 are available in
the include and linking paths.
*/
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#include <math.h>
#include <fftw3.h>
static const double PI = 4 * atan(1.0);
return exp(a*log(x));
}
double magnitude(double a, double b) {
return sqrt(a*a + b*b);
}
void velocityComponent( const int N,
const int dir,
const double kp,
const double u0,
double* const uvel )
{
long N3 = N*N*N;
long i,j,k;
double kk = sqrt(3 * (N/2)*(N/2));
int kkmax = (int) kk;
fftw_complex *uhat = (fftw_complex*) fftw_malloc(N3 * sizeof(fftw_complex));
fftw_complex *u = (fftw_complex*) fftw_malloc(N3 * sizeof(fftw_complex));
fftw_plan inv_trans_u;
inv_trans_u = fftw_plan_dft_3d(N, N, N, uhat, u, 1, FFTW_MEASURE);
/* Specifying the velocities in Fourier space */
for (i=0; i<N3; i++) uhat[i][0] = uhat[i][1] = 0.0;
for (i = 1; i < N/2; i++){
for (j = 0; j < N/2; j++){
for (k = 0; k < N/2; k++){
double kk = sqrt(i*i + j*j + k*k);
double th1 = 2*PI * ((double)rand())/((double)RAND_MAX);
double th2 = 2*PI * ((double)rand())/((double)RAND_MAX);
double phi1 = 2*PI * ((double)rand())/((double)RAND_MAX);
double E = 16.0 * sqrt(2.0/PI) * (u0*u0/kp) * raiseto(kk/kp, 4.0)
* exp(-2.0*(kk/kp)*(kk/kp));
double alfa_real = sqrt(E/(4*PI*kk*kk))*cos(th1)*cos(phi1);
double alfa_imag = sqrt(E/(4*PI*kk*kk))*sin(th1)*cos(phi1);
double beta_real = sqrt(E/(4*PI*kk*kk))*cos(th2)*sin(phi1);
double beta_imag = sqrt(E/(4*PI*kk*kk))*sin(th2)*sin(phi1);
if (dir == 0) {
uhat[k+N*(j+N*i)][0] = (alfa_real*kk*j+beta_real*i*k)/(kk*sqrt(i*i+j*j));
uhat[k+N*(j+N*i)][1] = (alfa_imag*kk*j+beta_imag*i*k)/(kk*sqrt(i*i+j*j));
} else if (dir == 1) {
uhat[k+N*(j+N*i)][0] = (beta_real*j*k-alfa_real*kk*i)/(kk*sqrt(i*i+j*j));
uhat[k+N*(j+N*i)][1] = (beta_imag*j*k-alfa_imag*kk*i)/(kk*sqrt(i*i+j*j));
} else {
uhat[k+N*(j+N*i)][0] = -(beta_real*sqrt(i*i+j*j))/kk;
uhat[k+N*(j+N*i)][1] = -(beta_imag*sqrt(i*i+j*j))/kk;
}
}
}
}
for (i = 0; i < 1; i++){
for (k = 0; k < N/2; k++){
for (j = 1; j < N/2; j++){
double kk = sqrt(i*i + j*j + k*k);
double th1 = 2*PI * ((double)rand())/((double)RAND_MAX);
double th2 = 2*PI * ((double)rand())/((double)RAND_MAX);
double phi1 = 2*PI * ((double)rand())/((double)RAND_MAX);
double E = 16.0 * sqrt(2.0/PI) * (u0*u0/kp) * raiseto(kk/kp, 4.0)
* exp(-2.0*(kk/kp)*(kk/kp));
double alfa_real = sqrt(E/(4*PI*kk*kk))*cos(th1)*cos(phi1);
double alfa_imag = sqrt(E/(4*PI*kk*kk))*sin(th1)*cos(phi1);
double beta_real = sqrt(E/(4*PI*kk*kk))*cos(th2)*sin(phi1);
double beta_imag = sqrt(E/(4*PI*kk*kk))*sin(th2)*sin(phi1);
if (dir == 0) {
uhat[k+N*(j+N*i)][0] = (alfa_real*kk*j+beta_real*i*k)/(kk*sqrt(i*i+j*j));
uhat[k+N*(j+N*i)][1] = (alfa_imag*kk*j+beta_imag*i*k)/(kk*sqrt(i*i+j*j));
} else if (dir == 1) {
uhat[k+N*(j+N*i)][0] = (beta_real*j*k-alfa_real*kk*i)/(kk*sqrt(i*i+j*j));
uhat[k+N*(j+N*i)][1] = (beta_imag*j*k-alfa_imag*kk*i)/(kk*sqrt(i*i+j*j));
} else {
uhat[k+N*(j+N*i)][0] = -(beta_real*sqrt(i*i+j*j))/kk;
uhat[k+N*(j+N*i)][1] = -(beta_imag*sqrt(i*i+j*j))/kk;
}
}
}
}
for (i = 0; i < 1; i++){
for (j = 0; j < 1; j++){
for (k = 0; k < N/2; k++){
uhat[k+N*(j+N*i)][0] = 0;
uhat[k+N*(j+N*i)][1] = 0;
}
}
}
/* The following is necessary to ensure that the inverse Fourier
transform yields a real velocity field with zero imaginary
components */
for (i=N/2+1; i<N; i++) {
for (j=N/2+1; j<N; j++) {
for (k=N/2+1; k<N; k++) {
uhat[k+N*(j+N*i)][0] = uhat[(N-k)+N*((N-j)+N*(N-i))][0];
uhat[k+N*(j+N*i)][1] = -uhat[(N-k)+N*((N-j)+N*(N-i))][1];
}
}
}
for (i=N/2+1; i<N; i++) {
for (j=N/2+1; j<N; j++) {
for (k=0; k<1; k++) {
uhat[k+N*(j+N*i)][0] = uhat[k+N*((N-j)+N*(N-i))][0];
uhat[k+N*(j+N*i)][1] = -uhat[k+N*((N-j)+N*(N-i))][1];
}
}
}
for (i=N/2+1; i<N; i++) {
for (j=0; j<1; j++) {
for (k=N/2+1; k<N; k++) {
uhat[k+N*(j+N*i)][0] = uhat[(N-k)+N*(j+N*(N-i))][0];
uhat[k+N*(j+N*i)][1] = -uhat[(N-k)+N*(j+N*(N-i))][1];
}
}
}
for (i=0; i<1; i++) {
for (j=N/2+1; j<N; j++) {
for (k=N/2+1; k<N; k++) {
uhat[k+N*(j+N*i)][0] = uhat[(N-k)+N*((N-j)+N*i)][0];
uhat[k+N*(j+N*i)][1] = -uhat[(N-k)+N*((N-j)+N*i)][1];
}
}
}
for (i=0; i<1; i++) {
for (j=0; j<1; j++) {
for (k=N/2+1; k<N; k++) {
uhat[k+N*(j+N*i)][0] = uhat[(N-k)+N*(j+N*i)][0];
uhat[k+N*(j+N*i)][1] = -uhat[(N-k)+N*(j+N*i)][1];
}
}
}
for (i=0; i<1; i++) {
for (j=N/2+1; j<N; j++) {
for (k=0; k<1; k++) {
uhat[k+N*(j+N*i)][0] = uhat[k+N*((N-j)+N*i)][0];
uhat[k+N*(j+N*i)][1] = -uhat[k+N*((N-j)+N*i)][1];
}
}
}
for (i=N/2+1; i<N; i++) {
for (j=0; j<1; j++) {
for (k=0; k<1; k++) {
uhat[k+N*(j+N*i)][0] = uhat[k+N*(j+N*(N-i))][0];
uhat[k+N*(j+N*i)][1] = -uhat[k+N*(j+N*(N-i))][1];
}
}
}
/* Inverse Fourier transform */
fftw_execute(inv_trans_u);
fftw_free(uhat);
fftw_destroy_plan(inv_trans_u);
double imag_velocity = 0;
for (i = 0; i < N3; i++){
double uu = u[i][1];
imag_velocity += (uu*uu);
}
imag_velocity = sqrt(imag_velocity / ((double)N3));
printf("RMS of imaginary component of computed velocity: %1.6e\n",imag_velocity);
for (i = 0; i < N3; i++){
uvel[i] = u[i][0];
}
fftw_free(u);
return;
}
void setVelocityField(const int N,
double* const uvel,
double* const vvel,
double* const wvel )
{
double kp = 4.0;
double u0 = 0.3;
long N3 = N*N*N;
long i,j,k;
double dx = 2*PI / ((double)N);
velocityComponent( N, 0, kp, u0, uvel );
velocityComponent( N, 1, kp, u0, vvel );
velocityComponent( N, 2, kp, u0, wvel );
double rms_velocity = 0;
for (i = 0; i < N3; i++){
double uu, vv, ww;
uu = uvel[i];
vv = vvel[i];
ww = wvel[i];
rms_velocity += (uu*uu + vv*vv + ww*ww);
}
rms_velocity = sqrt(rms_velocity / (3*((double)N3)));
/* scale the velocity components so that rms velocity matches u0 */
double factor = u0 / rms_velocity;
printf("Scaling factor = %1.16E\n",factor);
for (i = 0; i < N3; i++){
uvel[i] *= factor;
vvel[i] *= factor;
wvel[i] *= factor;
}
rms_velocity = 0;
for (i = 0; i < N3; i++){
double uu, vv, ww;
uu = uvel[i];
vv = vvel[i];
ww = wvel[i];
rms_velocity += (uu*uu + vv*vv + ww*ww);
}
rms_velocity = sqrt(rms_velocity / (3*((double)N3)));
printf("RMS velocity (component-wise): %1.16E\n",rms_velocity);
/* calculate the divergence of velocity */
double DivergenceNorm = 0;
for (i=0; i<N; i++) {
for (j=0; j<N; j++) {
for (k=0; k<N; k++) {
double u1, u2, v1, v2, w1, w2;
u1 = (i==0 ? uvel[k+N*(j+N*(N-1))] : uvel[k+N*(j+N*(i-1))] );
u2 = (i==N-1 ? uvel[k+N*(j+N*(0 ))] : uvel[k+N*(j+N*(i+1))] );
v1 = (j==0 ? vvel[k+N*((N-1)+N*i)] : vvel[k+N*((j-1)+N*i)] );
v2 = (j==N-1 ? vvel[k+N*((0 )+N*i)] : vvel[k+N*((j+1)+N*i)] );
w1 = (k==0 ? wvel[(N-1)+N*(j+N*i)] : wvel[(k-1)+N*(j+N*i)] );
w2 = (k==N-1 ? wvel[(0 )+N*(j+N*i)] : wvel[(k+1)+N*(j+N*i)] );
double Divergence = ( (u2-u1) + (v2-v1) + (w2-w1) ) / (2.0*dx);
DivergenceNorm += (Divergence*Divergence);
}
}
}
DivergenceNorm = sqrt(DivergenceNorm / ((double)N3));
printf("Velocity divergence: %1.16E\n",DivergenceNorm);
/* calculate the Taylor microscales */
double TaylorMicroscale[3];
double Numerator[3] = {0,0,0};
double Denominator[3] = {0,0,0};
for (i=0; i<N; i++) {
for (j=0; j<N; j++) {
for (k=0; k<N; k++) {
double u1, u2, uu, v1, v2, vv, w1, w2, ww;
u1 = (i==0 ? uvel[k+N*(j+N*(N-1))] : uvel[k+N*(j+N*(i-1))] );
u2 = (i==N-1 ? uvel[k+N*(j+N*(0 ))] : uvel[k+N*(j+N*(i+1))] );
v1 = (j==0 ? vvel[k+N*((N-1)+N*i)] : vvel[k+N*((j-1)+N*i)] );
v2 = (j==N-1 ? vvel[k+N*((0 )+N*i)] : vvel[k+N*((j+1)+N*i)] );
w1 = (k==0 ? wvel[(N-1)+N*(j+N*i)] : wvel[(k-1)+N*(j+N*i)] );
w2 = (k==N-1 ? wvel[(0 )+N*(j+N*i)] : wvel[(k+1)+N*(j+N*i)] );
uu = uvel[k+N*(j+N*i)];
vv = vvel[k+N*(j+N*i)];
ww = wvel[k+N*(j+N*i)];
double du, dv, dw;
du = (u2 - u1) / (2.0*dx);
dv = (v2 - v1) / (2.0*dx);
dw = (w2 - w1) / (2.0*dx);
Numerator[0] += (uu*uu);
Numerator[1] += (vv*vv);
Numerator[2] += (ww*ww);
Denominator[0] += (du*du);
Denominator[1] += (dv*dv);
Denominator[2] += (dw*dw);
}
}
}
Numerator[0] /= (N*N*N); Denominator[0] /= (N*N*N);
Numerator[1] /= (N*N*N); Denominator[1] /= (N*N*N);
Numerator[2] /= (N*N*N); Denominator[2] /= (N*N*N);
TaylorMicroscale[0] = sqrt(Numerator[0]/Denominator[0]);
TaylorMicroscale[1] = sqrt(Numerator[1]/Denominator[1]);
TaylorMicroscale[2] = sqrt(Numerator[2]/Denominator[2]);
printf("Taylor microscales: %1.16E, %1.16E, %1.16E\n",
TaylorMicroscale[0],TaylorMicroscale[1],TaylorMicroscale[2]);
return;
}
int main()
{
FILE *out, *in;
int NI,NJ,NK,ndims;
char ip_file_type[50];
strcpy(ip_file_type,"ascii");
printf("Reading file \"solver.inp\"...\n");
in = fopen("solver.inp","r");
if (!in) printf("Error: Input file \"solver.inp\" not found. Default values will be used.\n");
else {
char word[500];
fscanf(in,"%s",word);
if (!strcmp(word, "begin")){
while (strcmp(word, "end")){
fscanf(in,"%s",word);
if (!strcmp(word, "ndims")) fscanf(in,"%d",&ndims);
else if (!strcmp(word, "size")) {
fscanf(in,"%d",&NI);
fscanf(in,"%d",&NJ);
fscanf(in,"%d",&NK);
} else if (!strcmp(word, "ip_file_type")) fscanf(in,"%s",ip_file_type);
}
} else printf("Error: Illegal format in solver.inp. Crash and burn!\n");
}
fclose(in);
if (ndims != 3) {
printf("ndims is not 3 in solver.inp. this code is to generate 3D exact conditions\n");
return(0);
}
printf("Grid:\t\t\t%d x %d x %d\n",NI,NJ,NK);
if ((NI != NJ) || (NI != NK) || (NJ != NK)) {
printf("Error: NI,NJ,NK not equal. Bye!\n");
return(0);
}
int N = NI;
long N3 = N*N*N;
int i,j,k;
double dx = 2*PI / ((double)N);
/* Calculating the velocity components through a Fourier transform */
double* u = (double*) calloc (N3, sizeof(double));
double* v = (double*) calloc (N3, sizeof(double));
double* w = (double*) calloc (N3, sizeof(double));
setVelocityField(N, u, v, w);
/* grid and solution in conserved variable form */
double *x,*y,*z,*U;
x = (double*) calloc (N, sizeof(double));
y = (double*) calloc (N, sizeof(double));
z = (double*) calloc (N, sizeof(double));
U = (double*) calloc (5*N3, sizeof(double));
for (i = 0; i < N; i++){
for (j = 0; j < N; j++){
for (k = 0; k < N; k++){
x[i] = i*dx;
y[j] = j*dx;
z[k] = k*dx;
double RHO, uvel, vvel, wvel, P;
RHO = 1.0;
uvel = u[k+N*(j+N*i)];
vvel = v[k+N*(j+N*i)];
wvel = w[k+N*(j+N*i)];
P = 1.0/1.4;
long p = i + N*j + N*N*k;
U[5*p+0] = RHO;
U[5*p+1] = RHO*uvel;
U[5*p+2] = RHO*vvel;
U[5*p+3] = RHO*wvel;
U[5*p+4] = P/0.4 + 0.5 * RHO * (uvel*uvel + vvel*vvel + wvel*wvel);
}
}
}
free(u);
free(v);
free(w);
FILE *op;
if (!strcmp(ip_file_type,"ascii")) {
printf("Writing ASCII initial solution file initial.inp\n");
op = fopen("initial.inp","w");
for (i = 0; i < N; i++) fprintf(op,"%1.16E ",x[i]);
fprintf(op,"\n");
for (j = 0; j < N; j++) fprintf(op,"%1.16E ",y[j]);
fprintf(op,"\n");
for (k = 0; k < N; k++) fprintf(op,"%1.16E ",z[k]);
fprintf(op,"\n");
for (i = 0; i < N; i++) {
for (j = 0; j < N; j++) {
for (k = 0; k < N; k++) {
int p = i + N*j + N*N*k;
fprintf(op,"%1.16E ",U[5*p+0]);
}
}
}
fprintf(op,"\n");
for (i = 0; i < N; i++) {
for (j = 0; j < N; j++) {
for (k = 0; k < N; k++) {
int p = i + N*j + N*N*k;
fprintf(op,"%1.16E ",U[5*p+1]);
}
}
}
fprintf(op,"\n");
for (i = 0; i < N; i++) {
for (j = 0; j < N; j++) {
for (k = 0; k < N; k++) {
int p = i + N*j + N*N*k;
fprintf(op,"%1.16E ",U[5*p+2]);
}
}
}
fprintf(op,"\n");
for (i = 0; i < N; i++) {
for (j = 0; j < N; j++) {
for (k = 0; k < N; k++) {
int p = i + N*j + N*N*k;
fprintf(op,"%1.16E ",U[5*p+3]);
}
}
}
fprintf(op,"\n");
for (i = 0; i < N; i++) {
for (j = 0; j < N; j++) {
for (k = 0; k < N; k++) {
int p = i + N*j + N*N*k;
fprintf(op,"%1.16E ",U[5*p+4]);
}
}
}
fprintf(op,"\n");
fclose(op);
} else if ((!strcmp(ip_file_type,"binary")) || (!strcmp(ip_file_type,"bin"))) {
printf("Writing binary initial solution file initial.inp\n");
op = fopen("initial.inp","wb");
fwrite(x,sizeof(double),N,op);
fwrite(y,sizeof(double),N,op);
fwrite(z,sizeof(double),N,op);
fwrite(U,sizeof(double),5*N3,op);
fclose(op);
}
free(x);
free(y);
free(z);
free(U);
return(0);
}
Output:
Note that iproc is set to
2 2 1
in solver.inp (i.e., 2 processors along x, 2 processors along y, and 1 processor along z). Thus, this example should be run with 4 MPI ranks (or change iproc).
After running the code, there should be 11 output files op_00000.bin, op_00001.bin, ... op_00010.bin; the first one is the solution at \(t=0\) and the final one is the solution at \(t=5\). Since HyPar::op_overwrite is set to no in solver.inp, separate files are written for solutions at each output time. All the files are binary (HyPar::op_file_format is set to binary in solver.inp).
To generate compute the energy spectrum from a given solution, compile and run the following code in the run directory. This code wants to read a file called op.bin, so make a symbolic link with that name pointing to the solution file whose energy spectrum is to be computed. (If HyPar::op_overwrite is set to yes in solver.inp, then the solution file itself is called op.bin). Also note that the solution must be in binary format (HyPar::op_file_format must be binary in solver.inp). It will write out a ASCII text file spectrum.dat with two columns: \(k\) and \(E\left(k\right)\). Note: this code requires the FFTW library installed (http://www.fftw.org/). To compile:
gcc -I/path/to/fftw3.h -L/path/to/libfftw3.a -lfftw3 fourier.c
(see the FFTW website on ways to install it).
/*
This code computes the energy spectrum of a 3D compressible flow
solution.
+ The grid dimensions must be the same in all three dimensions.
+ The solution must be in HyPar's binary solution format.
+ This code looks for "op.bin"; if the simulation was unsteady with
multiple "op_<idx>.bin" files, create a symbolic link named "op.bin"
pointing to the specific "op_<idx>.bin" solution file for which the
spectrum should be computed.
This code requires the FFTW3 library (https://www.fftw.org/). Make sure
the fftw3.h and libfftw3 are available in the include and linking paths.
*/
#include <string.h>
#include <stdlib.h>
#include <math.h>
#include <fftw3.h>
void fourierTransform( const long N,
double* const uu,
fftw_complex* const uhat )
{
long i,j,k;
long N3 = N*N*N;
fftw_complex *u = (fftw_complex*) fftw_malloc(N3 * sizeof(fftw_complex));
fftw_plan transform_u;
transform_u = fftw_plan_dft_3d(N, N, N, u, uhat, -1, FFTW_MEASURE);
for (i = 0; i < N; i++){
for (j = 0; j < N; j++){
for (k = 0; k < N; k++){
u[k+N*(j+N*i)][0] = uu[k+N*(j+N*i)];
u[k+N*(j+N*i)][1] = 0;
}
}
}
fftw_execute(transform_u);
fftw_free(u);
for (i = 0; i < N; i++){
for (j = 0; j < N; j++){
for (k = 0; k < N; k++){
uhat[k+N*(j+N*i)][0] /= ((double)N3);
uhat[k+N*(j+N*i)][1] /= ((double)N3);
}
}
}
fftw_destroy_plan(transform_u);
return;
}
void energySpectrum(const long N,
const fftw_complex* const uhat,
const fftw_complex* const vhat,
const fftw_complex* const what )
{
long i,j,k;
long N3 = N*N*N;
double kk = sqrt(3 * (N/2)*(N/2));
int kkmax = (int) kk;
double *freq = (double*) calloc(kkmax+1, sizeof(double));
double *Eng = (double*) calloc(kkmax+1, sizeof(double));
double total_energy = 0.0;
for (i = 0; i < N; i++){
for (j = 0; j < N; j++){
for (k = 0; k < N; k++){
long p = k+N*(j+N*i);
long isq, jsq, ksq;
if (i > N/2) isq = (i-N) * (i-N);
else isq = i*i;
if (j > N/2) jsq = (j-N) * (j-N);
else jsq = j*j;
if (k > N/2) ksq = (k-N) * (k-N);
else ksq = k*k;
double kk = sqrt(isq + jsq + ksq);
freq[(int)kk] = kk;
Eng[(int)kk] = Eng[(int)kk]
+ 0.5 * ( (uhat[p][0]*uhat[p][0] + uhat[p][1]*uhat[p][1])
+ (vhat[p][0]*vhat[p][0] + vhat[p][1]*vhat[p][1])
+ (what[p][0]*what[p][0] + what[p][1]*what[p][1]) );
total_energy = total_energy
+ 0.5 * ( (uhat[p][0]*uhat[p][0] + uhat[p][1]*uhat[p][1])
+ (vhat[p][0]*vhat[p][0] + vhat[p][1]*vhat[p][1])
+ (what[p][0]*what[p][0] + what[p][1]*what[p][1]) );
}
}
}
printf("Total Energy: %1.16E\n",total_energy);
FILE *out;
out = fopen("spectrum.dat","w");
for (i = 1; i < kkmax; i++) fprintf(out,"%1.16E\t%1.16E\n",freq[i],Eng[i]/total_energy);
fclose(out);
free(freq);
free(Eng);
return;
}
int main()
{
long i,j,k;
int NI,NJ,NK;
char op_file_format[50];
FILE *in;
printf("Reading file \"solver.inp\"...\n");
in = fopen("solver.inp","r");
if (!in) {
printf("Error: Input file \"solver.inp\" not found.\n");
return(0);
} else {
char word[500];
fscanf(in,"%s",word);
if (!strcmp(word, "begin")){
while (strcmp(word, "end")){
fscanf(in,"%s",word);
if (!strcmp(word, "size")) {
fscanf(in,"%d",&NI);
fscanf(in,"%d",&NJ);
fscanf(in,"%d",&NK);
} else if (!strcmp(word, "op_file_format")) fscanf(in,"%s",op_file_format);
}
} else printf("Error: Illegal format in solver.inp. Crash and burn!\n");
}
fclose(in);
printf("Grid size: %d x %d x %d.\n",NI,NJ,NK);
long N = NI;
long N3 = N*N*N;
if ((!strcmp(op_file_format,"binary")) || (!strcmp(op_file_format,"bin"))) {
FILE *inp;
double *x = (double*) calloc (N,sizeof(double));
double *y = (double*) calloc (N,sizeof(double));
double *z = (double*) calloc (N,sizeof(double));
double *U = (double*) calloc (5*N3,sizeof(double));
int ndims, nvars, dims[3];
double *u,*v,*w;
u = (double*) calloc (N3, sizeof(double));
v = (double*) calloc (N3, sizeof(double));
w = (double*) calloc (N3, sizeof(double));
printf("Reading binary solution file op.bin\n");
inp = fopen("op.bin","rb");
if (!inp) {
printf("Output file op.bin not found!\n");
return(0);
}
fread(&ndims,sizeof(int),1,inp);
fread(&nvars,sizeof(int),1,inp);
fread(dims,sizeof(int),3,inp);
fread(x,sizeof(double),N,inp);
fread(y,sizeof(double),N,inp);
fread(z,sizeof(double),N,inp);
fread(U,sizeof(double),5*N3,inp);
fclose(inp);
for (i=0; i<N; i++) {
for (j=0; j<N; j++) {
for (k=0; k<N; k++) {
long p1 = 5*(i+N*(j+N*k));
long p2 = k+N*(j+N*i);
double rho = U[p1];
u[p2] = U[p1+1]/rho;
v[p2] = U[p1+2]/rho;
w[p2] = U[p1+3]/rho;
}
}
}
free(x);
free(y);
free(z);
free(U);
double rms_velocity = 0;
for (i = 0; i < N; i++) {
for (j = 0; j < N; j++) {
for (k = 0; k < N; k++) {
long p = k+N*(j+N*i);
rms_velocity += (u[p]*u[p] + v[p]*v[p] + w[p]*w[p]);
}
}
}
rms_velocity = sqrt(rms_velocity / (3*((double)N3)));
printf("RMS velocity (component-wise): %1.16E\n",rms_velocity);
/* calculate the divergence of velocity */
double pi = 4.0*atan(1.0);
double dx = 2*pi / ((double)N);
double DivergenceNorm = 0;
for (i=0; i<N; i++) {
for (j=0; j<N; j++) {
for (k=0; k<N; k++) {
double u1, u2, v1, v2, w1, w2;
u1 = (i==0 ? u[k+N*(j+N*(N-1))] : u[k+N*(j+N*(i-1))] );
u2 = (i==N-1 ? u[k+N*(j+N*(0 ))] : u[k+N*(j+N*(i+1))] );
v1 = (j==0 ? v[k+N*((N-1)+N*i)] : v[k+N*((j-1)+N*i)] );
v2 = (j==N-1 ? v[k+N*((0 )+N*i)] : v[k+N*((j+1)+N*i)] );
w1 = (k==0 ? w[(N-1)+N*(j+N*i)] : w[(k-1)+N*(j+N*i)] );
w2 = (k==N-1 ? w[(0 )+N*(j+N*i)] : w[(k+1)+N*(j+N*i)] );
double Divergence = ( (u2-u1) + (v2-v1) + (w2-w1) ) / (2.0*dx);
DivergenceNorm += (Divergence*Divergence);
}
}
}
DivergenceNorm = sqrt(DivergenceNorm / ((double)N3));
printf("Velocity divergence: %1.16E\n",DivergenceNorm);
/* calculate the Taylor microscales */
double TaylorMicroscale[3];
double Numerator[3] = {0,0,0};
double Denominator[3] = {0,0,0};
for (i=0; i<N; i++) {
for (j=0; j<N; j++) {
for (k=0; k<N; k++) {
double u1, u2, uc, v1, v2, vc, w1, w2, wc;
u1 = (i==0 ? u[k+N*(j+N*(N-1))] : u[k+N*(j+N*(i-1))] );
u2 = (i==N-1 ? u[k+N*(j+N*(0 ))] : u[k+N*(j+N*(i+1))] );
v1 = (j==0 ? v[k+N*((N-1)+N*i)] : v[k+N*((j-1)+N*i)] );
v2 = (j==N-1 ? v[k+N*((0 )+N*i)] : v[k+N*((j+1)+N*i)] );
w1 = (k==0 ? w[(N-1)+N*(j+N*i)] : w[(k-1)+N*(j+N*i)] );
w2 = (k==N-1 ? w[(0 )+N*(j+N*i)] : w[(k+1)+N*(j+N*i)] );
uc = u[k+N*(j+N*i)];
vc = v[k+N*(j+N*i)];
wc = w[k+N*(j+N*i)];
double du, dv, dw;
du = (u2 - u1) / (2.0*dx);
dv = (v2 - v1) / (2.0*dx);
dw = (w2 - w1) / (2.0*dx);
Numerator[0] += (uc*uc);
Numerator[1] += (vc*vc);
Numerator[2] += (wc*wc);
Denominator[0] += (du*du);
Denominator[1] += (dv*dv);
Denominator[2] += (dw*dw);
}
}
}
Numerator[0] /= ((double)N3); Denominator[0] /= ((double)N3);
Numerator[1] /= ((double)N3); Denominator[1] /= ((double)N3);
Numerator[2] /= ((double)N3); Denominator[2] /= ((double)N3);
TaylorMicroscale[0] = sqrt(Numerator[0]/Denominator[0]);
TaylorMicroscale[1] = sqrt(Numerator[1]/Denominator[1]);
TaylorMicroscale[2] = sqrt(Numerator[2]/Denominator[2]);
printf("Taylor microscales: %1.16E, %1.16E, %1.16E\n",
TaylorMicroscale[0],TaylorMicroscale[1],TaylorMicroscale[2]);
fftw_complex *uhat = (fftw_complex*) fftw_malloc(N3 * sizeof(fftw_complex));
printf("Computing Fourier transform (u).\n");
fourierTransform( N, u, uhat );
free(u);
fftw_complex *vhat = (fftw_complex*) fftw_malloc(N3 * sizeof(fftw_complex));
printf("Computing Fourier transform (v).\n");
fourierTransform( N, v, vhat );
free(v);
fftw_complex *what = (fftw_complex*) fftw_malloc(N3 * sizeof(fftw_complex));
printf("Computing Fourier transform (w).\n");
fourierTransform( N, w, what );
free(w);
energySpectrum(N, uhat, vhat, what);
fftw_free(uhat);
fftw_free(vhat);
fftw_free(what);
} else {
printf("Error: Unsupported output file type. Use binary output only!\n");
}
return(0);
}
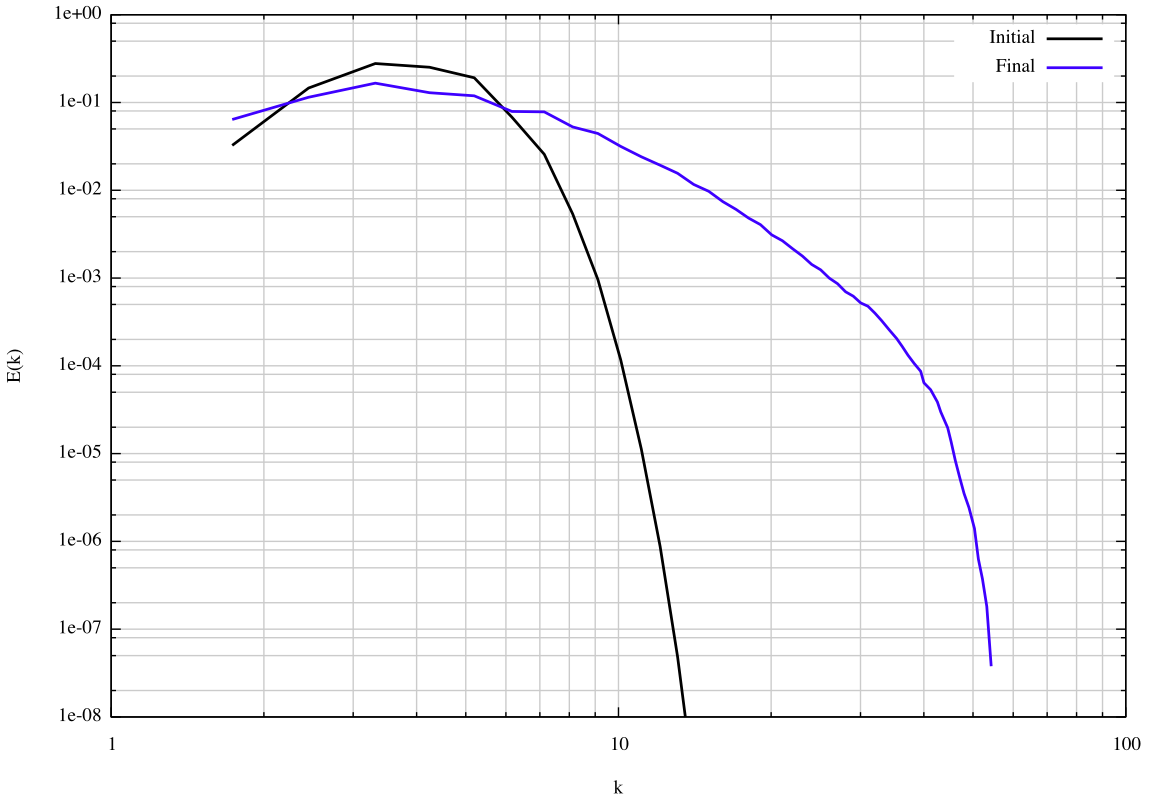
The following figure shows the initial and final (t=5) energy spectra:
The following file computes the kinetic energy as a function of time from the solution files. It writes out an ASCII text file energy.dat with two colums: time and kinetic energy.
/*
This code calculates the kinetic energy as
a function of time. It reads in the solution
files (assuming they are not overwritten and
are available as op_xxxxx.bin).
*/
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#include <math.h>
void IncrementFilename(char *f)
{
if (f[7] == '9') {
f[7] = '0';
if (f[6] == '9') {
f[6] = '0';
if (f[5] == '9') {
f[5] = '0';
if (f[4] == '9') {
f[4] = '0';
if (f[3] == '9') {
f[3] = '0';
fprintf(stderr,"Warning: file increment hit max limit. Resetting to zero.\n");
} else {
f[3]++;
}
} else {
f[4]++;
}
} else {
f[5]++;
}
} else {
f[6]++;
}
} else {
f[7]++;
}
}
int main()
{
FILE *out, *in, *inputs;
double dt;
int file_op_iter;
char filename[50], op_file_format[50];
inputs = fopen("solver.inp","r");
if (!inputs) {
fprintf(stderr,"Error: File \"solver.inp\" not found.\n");
return(1);
} else {
char word[100];
fscanf(inputs,"%s",word);
if (!strcmp(word, "begin")){
while (strcmp(word, "end")){
fscanf(inputs,"%s",word);
if (!strcmp(word, "dt" )) fscanf(inputs,"%lf",&dt );
else if (!strcmp(word, "op_file_format" )) fscanf(inputs,"%s" ,op_file_format);
else if (!strcmp(word, "file_op_iter" )) fscanf(inputs,"%d" ,&file_op_iter );
}
}
fclose(inputs);
}
if (strcmp(op_file_format,"binary") && strcmp(op_file_format,"bin")) {
printf("Error: solution output needs to be in binary files.\n");
return(0);
}
int count = 0;
double samay = 0.0;
out = fopen("energy.dat","w");
strcpy(filename,"op_00000.bin");
double energy0 = 1;
while(1) {
in = fopen(filename,"rb");
if (!in) {
printf("No more files found. Exiting.\n");
break;
} else {
printf("File %s.\n",filename);
int ndims, nvars, dims[3];
double energy = 0.0, *U,*x,*y,*z;
fread(&ndims,sizeof(int),1,in);
fread(&nvars,sizeof(int),1,in);
if (ndims != 3) {
printf("Error: ndims in %s not equal to 3!\n",filename);
return(0);
}
if (nvars != 5) {
printf("Error: nvars in %s not equal to 4!\n",filename);
return(0);
}
fread(dims,sizeof(int),ndims,in);
printf("Dimensions: %d x %d x %d\n",dims[0],dims[1],dims[2]);
int N = dims[0], N3 = N*N*N;
if ((dims[1] != N) || (dims[2] != N)) {
printf("Error: Unequal number of points in the 3 dimensions!\n");
return(0);
}
double pi = 4*atan(1.0);
double dx = 2*pi / (double)N;
double dx3 = dx*dx*dx;
x = (double*) calloc (N,sizeof(double));
y = (double*) calloc (N,sizeof(double));
z = (double*) calloc (N,sizeof(double));
U = (double*) calloc (N3*nvars,sizeof(double));
fread(x,sizeof(double),N,in);
fread(y,sizeof(double),N,in);
fread(z,sizeof(double),N,in);
fread(U,sizeof(double),N3*nvars,in);
int p;
for (p = 0; p < N3; p++) {
double rho, u, v, w;
rho = U[nvars*p];
u = U[nvars*p+1] / rho;
v = U[nvars*p+2] / rho;
w = U[nvars*p+3] / rho;
energy += ((u*u + v*v + w*w) * dx3);
}
energy /= 2.0;
/* non dimensionalize */
if (!count) energy0 = energy;
energy /= energy0;
free(U);
free(x);
free(y);
free(z);
fprintf(out, "%1.16E\t%1.16E\n", samay, energy);
fclose(in);
}
count++;
samay += (dt * (double)file_op_iter);
IncrementFilename(filename);
}
fclose(out);
return(0);
}
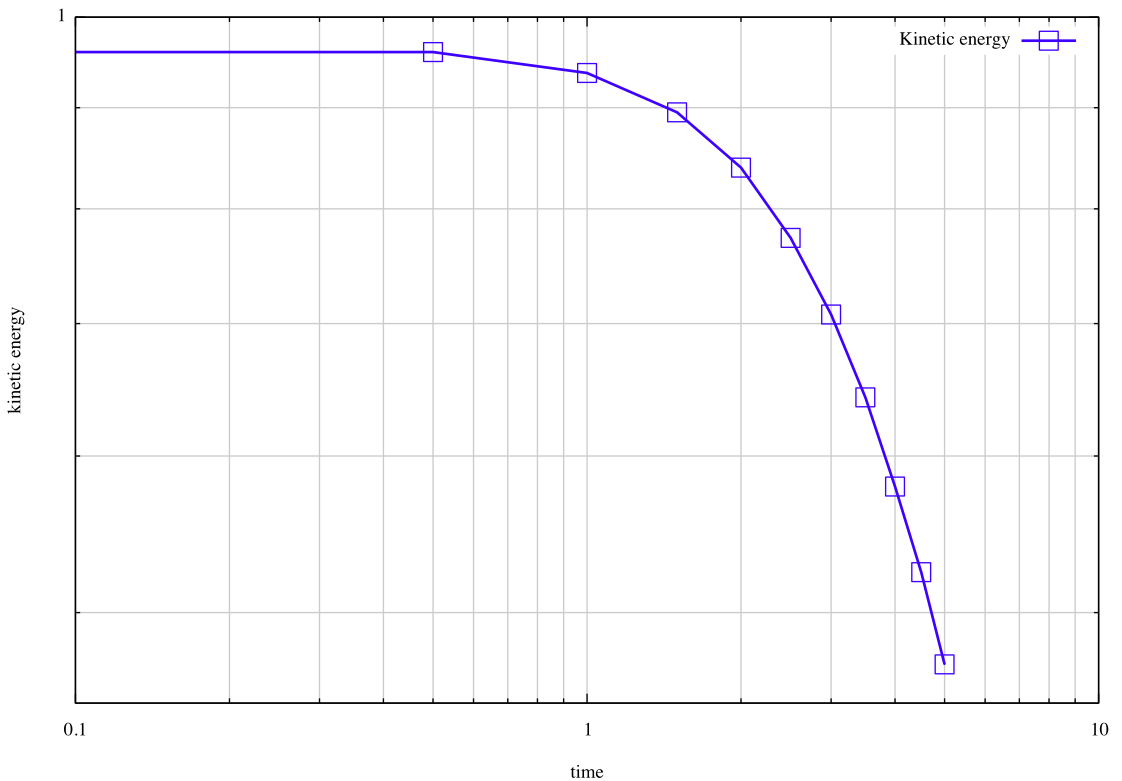
The following figure shows the kinetic energy decay:
The code hypar/Extras/BinaryToTecplot.c can be used to convert the binary solution files to 3D Tecplot files that can be visualized in any software supporting the Tecplot format. Similarly, the code hypar/Extras/BinaryToText.c can be used to convert the binary solution files to ASCII text files with the following data layout: the first three columns are grid indices, the next three columns are x, y, and z coordinates, and the remaining columns are the solution components ( \(\rho, \rho u, \rho v, \rho w, e\)).
The following figure shows the density iso-surface colored by the internal energy (plotted in ParaView after converting the binary solution to a Tecplot file):
Expected screen output:
HyPar - Parallel (MPI) version with 4 processes
Compiled with PETSc time integration.
Reading solver inputs from file "solver.inp".
No. of dimensions : 3
No. of variables : 5
Domain size : 64 64 64
Processes along each dimension : 2 2 1
No. of ghosts pts : 3
No. of iter. : 200
Restart iteration : 0
Time integration scheme : rk (44)
Spatial discretization scheme (hyperbolic) : crweno5
Split hyperbolic flux term? : no
Interpolation type for hyperbolic term : components
Spatial discretization type (parabolic ) : nonconservative-2stage
Spatial discretization scheme (parabolic ) : 4
Time Step : 2.500000E-02
Check for conservation : no
Screen output iterations : 10
File output iterations : 20
Initial solution file type : binary
Initial solution read mode : serial
Solution file write mode : serial
Solution file format : binary
Overwrite solution file : no
Physical model : navierstokes3d
Partitioning domain.
Allocating data arrays.
Reading array from binary file initial.inp (Serial mode).
Volume integral of the initial solution:
0: 2.4805021344266444E+02
1: 1.6653345369377348E-14
2: 1.3655743202889425E-14
3: -5.9952043329758453E-15
4: 4.7643358853329289E+02
Reading boundary conditions from "boundary.inp".
Boundary periodic: Along dimension 0 and face +1
Boundary periodic: Along dimension 0 and face -1
Boundary periodic: Along dimension 1 and face +1
Boundary periodic: Along dimension 1 and face -1
Boundary periodic: Along dimension 2 and face +1
Boundary periodic: Along dimension 2 and face -1
6 boundary condition(s) read.
Initializing solvers.
Reading WENO parameters from weno.inp.
Initializing physics. Model = "navierstokes3d"
Reading physical model inputs from file "physics.inp".
Setting up time integration.
Solving in time (from 0 to 200 iterations)
Writing solution file op_00000.bin.
Iteration: 10 Time: 2.500E-01 Max CFL: 6.276E-01 Max Diff. No.: -1.000E+00 Norm: 2.6011E-02
Iteration: 20 Time: 5.000E-01 Max CFL: 6.087E-01 Max Diff. No.: -1.000E+00 Norm: 2.5551E-02
Writing solution file op_00001.bin.
Iteration: 30 Time: 7.500E-01 Max CFL: 5.996E-01 Max Diff. No.: -1.000E+00 Norm: 2.6326E-02
Iteration: 40 Time: 1.000E+00 Max CFL: 5.768E-01 Max Diff. No.: -1.000E+00 Norm: 2.6866E-02
Writing solution file op_00002.bin.
Iteration: 50 Time: 1.250E+00 Max CFL: 5.808E-01 Max Diff. No.: -1.000E+00 Norm: 2.7645E-02
Iteration: 60 Time: 1.500E+00 Max CFL: 6.082E-01 Max Diff. No.: -1.000E+00 Norm: 2.7552E-02
Writing solution file op_00003.bin.
Iteration: 70 Time: 1.750E+00 Max CFL: 5.973E-01 Max Diff. No.: -1.000E+00 Norm: 2.7574E-02
Iteration: 80 Time: 2.000E+00 Max CFL: 5.832E-01 Max Diff. No.: -1.000E+00 Norm: 2.7398E-02
Writing solution file op_00004.bin.
Iteration: 90 Time: 2.250E+00 Max CFL: 5.770E-01 Max Diff. No.: -1.000E+00 Norm: 2.6709E-02
Iteration: 100 Time: 2.500E+00 Max CFL: 5.607E-01 Max Diff. No.: -1.000E+00 Norm: 2.6009E-02
Writing solution file op_00005.bin.
Iteration: 110 Time: 2.750E+00 Max CFL: 5.534E-01 Max Diff. No.: -1.000E+00 Norm: 2.5561E-02
Iteration: 120 Time: 3.000E+00 Max CFL: 5.698E-01 Max Diff. No.: -1.000E+00 Norm: 2.4610E-02
Writing solution file op_00006.bin.
Iteration: 130 Time: 3.250E+00 Max CFL: 5.288E-01 Max Diff. No.: -1.000E+00 Norm: 2.4219E-02
Iteration: 140 Time: 3.500E+00 Max CFL: 5.503E-01 Max Diff. No.: -1.000E+00 Norm: 2.3388E-02
Writing solution file op_00007.bin.
Iteration: 150 Time: 3.750E+00 Max CFL: 5.118E-01 Max Diff. No.: -1.000E+00 Norm: 2.2418E-02
Iteration: 160 Time: 4.000E+00 Max CFL: 5.156E-01 Max Diff. No.: -1.000E+00 Norm: 2.1473E-02
Writing solution file op_00008.bin.
Iteration: 170 Time: 4.250E+00 Max CFL: 4.965E-01 Max Diff. No.: -1.000E+00 Norm: 2.1132E-02
Iteration: 180 Time: 4.500E+00 Max CFL: 4.892E-01 Max Diff. No.: -1.000E+00 Norm: 2.0662E-02
Writing solution file op_00009.bin.
Iteration: 190 Time: 4.750E+00 Max CFL: 4.749E-01 Max Diff. No.: -1.000E+00 Norm: 1.9980E-02
Iteration: 200 Time: 5.000E+00 Max CFL: 4.787E-01 Max Diff. No.: -1.000E+00 Norm: 1.8848E-02
Writing solution file op_00010.bin.
Completed time integration (Final time: 5.000000).
Computed errors:
L1 Error : 0.0000000000000000E+00
L2 Error : 0.0000000000000000E+00
Linfinity Error : 0.0000000000000000E+00
Conservation Errors:
0.0000000000000000E+00
0.0000000000000000E+00
0.0000000000000000E+00
0.0000000000000000E+00
0.0000000000000000E+00
Solver runtime (in seconds): 1.4957965489999999E+03
Total runtime (in seconds): 1.4959968770000000E+03
Deallocating arrays.
Finished.