Location: hypar/Examples/1D/LinearDiffusion/SineWave_PETSc (This directory contains all the input files needed to run this case. If there is a Run.m, run it in MATLAB to quickly set up, run, and visualize the example).
Governing equations: 1D Linear Diffusion Equation (linearadr.h)
Domain: \(0 \le x < 1\), "periodic" (_PERIODIC_) boundary conditions
Initial solution: \(u\left(x,0\right) = \sin\left(2\pi x\right)\)
Numerical Method:
Input files required:
.petscrc
# See PETSc documentation for more details (https://petsc.org/release/overview/).
# Note that if the following are specified in this file, the corresponding inputs in solver.inp are *ignored*.
# + "-ts_dt" (time step size): ignores "dt" in solver.inp
# + "-ts_max_steps" (maximum number of time iterations): ignores "n_iter" in solver.inp
# + "-ts_max_time" (final simulation time): ignores "n_iter" X "dt" in solver.inp
# Use PETSc time-integration
-use-petscts
# Final time
-ts_max_time 10.0
# Time step size
-ts_dt 1.0
# Maximum number of iterations
-ts_max_steps 10
# Time integration scheme type - Crank-Nicholson
-ts_type cn
# No time-step adaptivity
-ts_adapt_type none
# Print time step information to screen
-ts_monitor
# For linear problens, tell nonlinear solver (SNES) to only use the linear solver (KSP)
-snes_type ksponly
# Print SNES iteration information to screen
-snes_monitor
# Linear solver (KSP) type
-ksp_type gmres
# Set relative tolerance
-ksp_rtol 1e-6
# Set absolute tolerance
-ksp_atol 1e-6
# Print KSP iteration information to screen
-ksp_monitor
solver.inp
begin
ndims 1
nvars 1
size 80
iproc 1
ghost 3
n_iter 200
time_scheme rk
time_scheme_type ssprk3
par_space_type conservative-1stage
par_space_scheme 2
dt 0.05
screen_op_iter 1
file_op_iter 2
op_file_format text
op_overwrite no
model linear-advection-diffusion-reaction
end
boundary.inp
2
periodic 0 1 0 0
periodic 0 -1 0 0
physics.inp
To generate initial.inp (initial solution) and exact.inp (exact solution), compile and run the following code in the run directory.
#include <stdio.h>
#include <stdlib.h>
#include <math.h>
#include <string.h>
double pi = 4.0*atan(1.0);
int NI,ndims,niter;
double nu, dt,final_time;
char ip_file_type[50];
strcpy(ip_file_type,"ascii");
FILE *in, *out;
printf("Reading file \"solver.inp\"...\n");
in = fopen("solver.inp","r");
if (!in) printf("Error: Input file \"solver.inp\" not found. Default values will be used.\n");
else {
char word[500];
fscanf(in,"%s",word);
if (!strcmp(word, "begin")){
while (strcmp(word, "end")){
fscanf(in,"%s",word);
if (!strcmp(word, "ndims")) fscanf(in,"%d",&ndims);
else if (!strcmp(word, "size")) fscanf(in,"%d",&NI);
else if (!strcmp(word, "dt")) fscanf(in,"%lf",&dt);
else if (!strcmp(word, "n_iter")) fscanf(in,"%d",&niter);
else if (!strcmp(word, "ip_file_type")) fscanf(in,"%s",ip_file_type);
}
} else printf("Error: Illegal format in solver.inp. Crash and burn!\n");
}
fclose(in);
if (ndims != 1) {
printf("ndims is not 1 in solver.inp. this code is to generate 1D initial conditions\n");
return(0);
}
printf("Grid:\t\t\t%d\n",NI);
final_time = (double)niter * dt;
printf("Final Time:\t\t\t%lf\n",final_time);
printf("Reading file \"physics.inp\"...\n");
in = fopen("physics.inp","r");
if (!in) {
printf("Error: Input file \"physics.inp\" not found. Default values will be used.\n");
nu = 1.0;
} else {
char word[500];
fscanf(in,"%s",word);
if (!strcmp(word, "begin")){
while (strcmp(word, "end")){
fscanf(in,"%s",word);
if (!strcmp(word,"diffusion")) fscanf(in,"%lf",&nu);
}
} else printf("Error: Illegal format in solver.inp. Crash and burn!\n");
}
fclose(in);
printf("Diffusion Coeff:\t\t\t%lf\n",nu);
int i;
double dx = 1.0 / ((double)NI);
double *x, *u;
x = (double*) calloc (NI, sizeof(double));
u = (double*) calloc (NI, sizeof(double));
for (i = 0; i < NI; i++) x[i] = i*dx;
for (i = 0; i < NI; i++) u[i] = sin(2*pi*x[i]);
if (!strcmp(ip_file_type,"ascii")) {
printf("Writing ASCII initial solution file initial.inp\n");
out = fopen("initial.inp","w");
for (i = 0; i < NI; i++) fprintf(out,"%lf ",x[i]);
fprintf(out,"\n");
for (i = 0; i < NI; i++) fprintf(out,"%lf ",u[i]);
fprintf(out,"\n");
fclose(out);
} else if ((!strcmp(ip_file_type,"binary")) || (!strcmp(ip_file_type,"bin"))) {
printf("Writing binary initial solution file initial.inp\n");
out = fopen("initial.inp","wb");
fwrite(x,sizeof(double),NI,out);
fwrite(u,sizeof(double),NI,out);
fclose(out);
}
for (i = 0; i < NI; i++) u[i] = exp(-nu*4*pi*pi*final_time)*sin(2*pi*x[i]);
if (!strcmp(ip_file_type,"ascii")) {
printf("Writing ASCII exact solution file exact.inp\n");
out = fopen("exact.inp","w");
for (i = 0; i < NI; i++) fprintf(out,"%lf ",x[i]);
fprintf(out,"\n");
for (i = 0; i < NI; i++) fprintf(out,"%lf ",u[i]);
fprintf(out,"\n");
fclose(out);
} else if ((!strcmp(ip_file_type,"binary")) || (!strcmp(ip_file_type,"bin"))) {
printf("Writing binary exact solution file exact.inp\n");
out = fopen("exact.inp","wb");
fwrite(x,sizeof(double),NI,out);
fwrite(u,sizeof(double),NI,out);
fclose(out);
}
free(x);
free(u);
return(0);
}
Output:
After running the code, there should be 6 output files op_00000.dat, op_00001.dat, ... op_00005.dat; the first one is the solution at \(t=0\) and the final one is the solution at \(t=10\). Since HyPar::op_overwrite is set to no in solver.inp, separate files are written for solutions at each output time. All the files are ASCII text (HyPar::op_file_format is set to text in solver.inp). In these files, the first column is grid index, the second column is x-coordinate, and the third column is the solution.
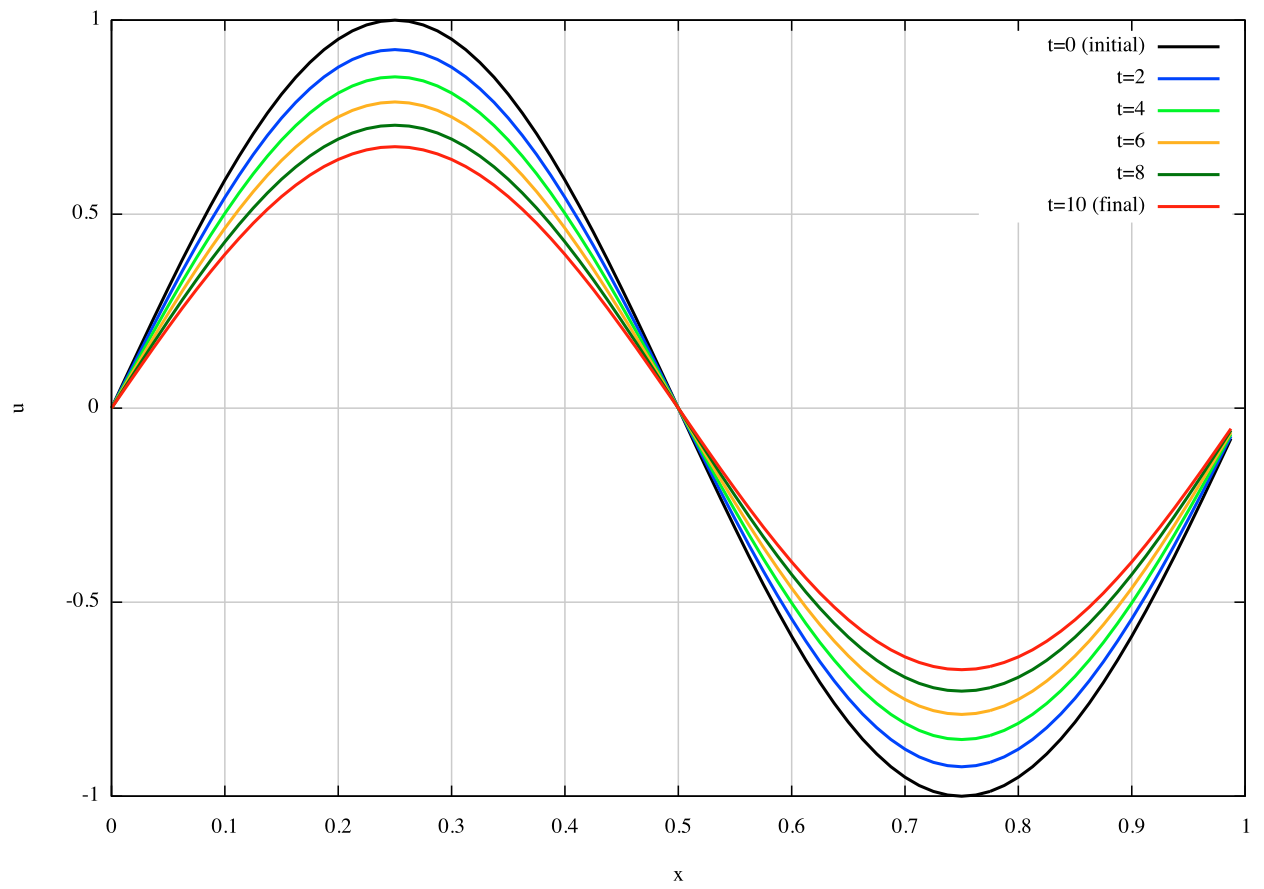
Solutions at t=0,2,4,6,8,10: The following figure is obtained by plotting the solution files.
Since the exact solution is available at the final time , the numerical errors are calculated and reported on screen (see below) as well as errors.dat:
80 1 5.0000000000000003E-02 1.5137204549144645E-04 1.5144589338237947E-04 1.5243229874191237E-04 4.7143999999999998E-02 4.7794999999999997E-02
The numbers are: number of grid points (HyPar::dim_global), number of processors (MPIVariables::iproc), time step size (HyPar::dt), L1, L2, and L-infinity errors (HyPar::error), solver wall time (seconds) (i.e., not accounting for initialization, and cleaning up), and total wall time.
Expected screen output:
HyPar - Parallel (MPI) version with 1 processes
Compiled with PETSc time integration.
Reading solver inputs from file "solver.inp".
No. of dimensions : 1
No. of variables : 1
Domain size : 80
Processes along each dimension : 1
No. of ghosts pts : 3
No. of iter. : 200
Restart iteration : 0
Time integration scheme : PETSc
Spatial discretization scheme (hyperbolic) : 1
Split hyperbolic flux term? : no
Interpolation type for hyperbolic term : characteristic
Spatial discretization type (parabolic ) : conservative-1stage
Spatial discretization scheme (parabolic ) : 2
Time Step : 5.000000E-02
Check for conservation : no
Screen output iterations : 1
File output iterations : 2
Initial solution file type : ascii
Initial solution read mode : serial
Solution file write mode : serial
Solution file format : text
Overwrite solution file : no
Physical model : linear-advection-diffusion-reaction
Partitioning domain.
Allocating data arrays.
Reading array from ASCII file initial.inp (Serial mode).
Volume integral of the initial solution:
0: 4.9005938196344800E-17
Reading boundary conditions from "boundary.inp".
Boundary periodic: Along dimension 0 and face +1
Boundary periodic: Along dimension 0 and face -1
2 boundary condition(s) read.
Initializing solvers.
Initializing physics. Model = "linear-advection-diffusion-reaction"
Reading physical model inputs from file "physics.inp".
Setting up PETSc time integration...
SolvePETSc(): Problem type is linear.
** Starting PETSc time integration **
0 TS dt 1. time 0.
Writing solution file op_00000.dat.
0 SNES Function norm 4.991102475213e-01
0 KSP Residual norm 4.991102475213e-01
1 KSP Residual norm 6.962037308773e-04
2 KSP Residual norm 1.012950664519e-04
3 KSP Residual norm 2.382699479453e-05
4 KSP Residual norm 8.138614230591e-06
5 KSP Residual norm 3.652734236012e-06
6 KSP Residual norm 1.609840186308e-06
7 KSP Residual norm 7.778170596475e-07
1 SNES Function norm 7.778170600692e-07
Iteration: 1 Time: 1.000E+00 Max CFL: 0.000E+00 Max Diff. No.: 6.400E+00
1 TS dt 1. time 1.
0 SNES Function norm 4.797973159676e-01
0 KSP Residual norm 4.797973159676e-01
1 KSP Residual norm 5.747952694550e-04
2 KSP Residual norm 7.833513076437e-05
3 KSP Residual norm 1.587336220931e-05
4 KSP Residual norm 4.761039329140e-06
5 KSP Residual norm 1.517295253640e-06
6 KSP Residual norm 6.546144957077e-07
1 SNES Function norm 6.546144952484e-07
Iteration: 2 Time: 2.000E+00 Max CFL: 0.000E+00 Max Diff. No.: 6.400E+00
Writing solution file op_00001.dat.
2 TS dt 1. time 2.
0 SNES Function norm 4.612316933851e-01
0 KSP Residual norm 4.612316933851e-01
1 KSP Residual norm 4.760016707446e-04
2 KSP Residual norm 6.149281763580e-05
3 KSP Residual norm 1.114455833715e-05
4 KSP Residual norm 3.343074822310e-06
5 KSP Residual norm 9.229640917063e-07
1 SNES Function norm 9.229640904854e-07
Iteration: 3 Time: 3.000E+00 Max CFL: 0.000E+00 Max Diff. No.: 6.400E+00
3 TS dt 1. time 3.
0 SNES Function norm 4.433844626305e-01
0 KSP Residual norm 4.433844626305e-01
1 KSP Residual norm 3.951724854780e-04
2 KSP Residual norm 4.870300472616e-05
3 KSP Residual norm 8.299367349374e-06
4 KSP Residual norm 2.673156368775e-06
5 KSP Residual norm 7.404350895583e-07
1 SNES Function norm 7.404350894310e-07
Iteration: 4 Time: 4.000E+00 Max CFL: 0.000E+00 Max Diff. No.: 6.400E+00
Writing solution file op_00002.dat.
4 TS dt 1. time 4.
0 SNES Function norm 4.262278256223e-01
0 KSP Residual norm 4.262278256223e-01
1 KSP Residual norm 3.287185349798e-04
2 KSP Residual norm 3.878782382748e-05
3 KSP Residual norm 6.181508465594e-06
4 KSP Residual norm 2.110463908832e-06
5 KSP Residual norm 5.886855585289e-07
1 SNES Function norm 5.886855576014e-07
Iteration: 5 Time: 5.000E+00 Max CFL: 0.000E+00 Max Diff. No.: 6.400E+00
5 TS dt 1. time 5.
0 SNES Function norm 4.097350599672e-01
0 KSP Residual norm 4.097350599672e-01
1 KSP Residual norm 2.739121699615e-04
2 KSP Residual norm 3.104320623701e-05
3 KSP Residual norm 4.612245458924e-06
4 KSP Residual norm 1.636117384369e-06
5 KSP Residual norm 4.628709620414e-07
1 SNES Function norm 4.628709605356e-07
Iteration: 6 Time: 6.000E+00 Max CFL: 0.000E+00 Max Diff. No.: 6.400E+00
Writing solution file op_00003.dat.
6 TS dt 1. time 6.
0 SNES Function norm 3.938804773094e-01
0 KSP Residual norm 3.938804773094e-01
1 KSP Residual norm 2.285909636229e-04
2 KSP Residual norm 2.495067888716e-05
3 KSP Residual norm 3.457387164788e-06
4 KSP Residual norm 1.240113460129e-06
5 KSP Residual norm 3.615990116765e-07
1 SNES Function norm 3.615990117171e-07
Iteration: 7 Time: 7.000E+00 Max CFL: 0.000E+00 Max Diff. No.: 6.400E+00
7 TS dt 1. time 7.
0 SNES Function norm 3.786393833109e-01
0 KSP Residual norm 3.786393833109e-01
1 KSP Residual norm 1.910271538593e-04
2 KSP Residual norm 2.012617663398e-05
3 KSP Residual norm 2.615125662104e-06
4 KSP Residual norm 9.189167436275e-07
1 SNES Function norm 9.189167435451e-07
Iteration: 8 Time: 8.000E+00 Max CFL: 0.000E+00 Max Diff. No.: 6.400E+00
Writing solution file op_00004.dat.
8 TS dt 1. time 8.
0 SNES Function norm 3.639880391862e-01
0 KSP Residual norm 3.639880391862e-01
1 KSP Residual norm 1.600091730000e-04
2 KSP Residual norm 1.630352171399e-05
3 KSP Residual norm 3.031522323873e-06
4 KSP Residual norm 1.236455894571e-06
5 KSP Residual norm 3.333920205313e-07
1 SNES Function norm 3.333920205967e-07
Iteration: 9 Time: 9.000E+00 Max CFL: 0.000E+00 Max Diff. No.: 6.400E+00
9 TS dt 1. time 9.
0 SNES Function norm 3.499036247089e-01
0 KSP Residual norm 3.499036247089e-01
1 KSP Residual norm 1.340160943955e-04
2 KSP Residual norm 1.301027023463e-05
3 KSP Residual norm 2.093675619948e-06
4 KSP Residual norm 8.678946259494e-07
1 SNES Function norm 8.678946260196e-07
Iteration: 10 Time: 1.000E+01 Max CFL: 0.000E+00 Max Diff. No.: 6.400E+00
Writing solution file op_00005.dat.
10 TS dt 1. time 10.
** Completed PETSc time integration **
Reading array from ASCII file exact.inp (Serial mode).
Computed errors:
L1 Error : 1.5137204549144645E-04
L2 Error : 1.5144589338237947E-04
Linfinity Error : 1.5243229874191237E-04
Conservation Errors:
0.0000000000000000E+00
Solver runtime (in seconds): 4.7143999999999998E-02
Total runtime (in seconds): 4.7794999999999997E-02
Deallocating arrays.
Finished.