Location: hypar/Examples/2D/LinearDiffusion/SineWave_PETSc (This directory contains all the input files needed to run this case. If there is a Run.m, run it in MATLAB to quickly set up, run, and visualize the example).

Governing equations: 2D Linear Diffusion Equation (linearadr.h)

Domain: \(0 \le x,y < 1\), "periodic" (_PERIODIC_) boundary conditions on all boundaries.

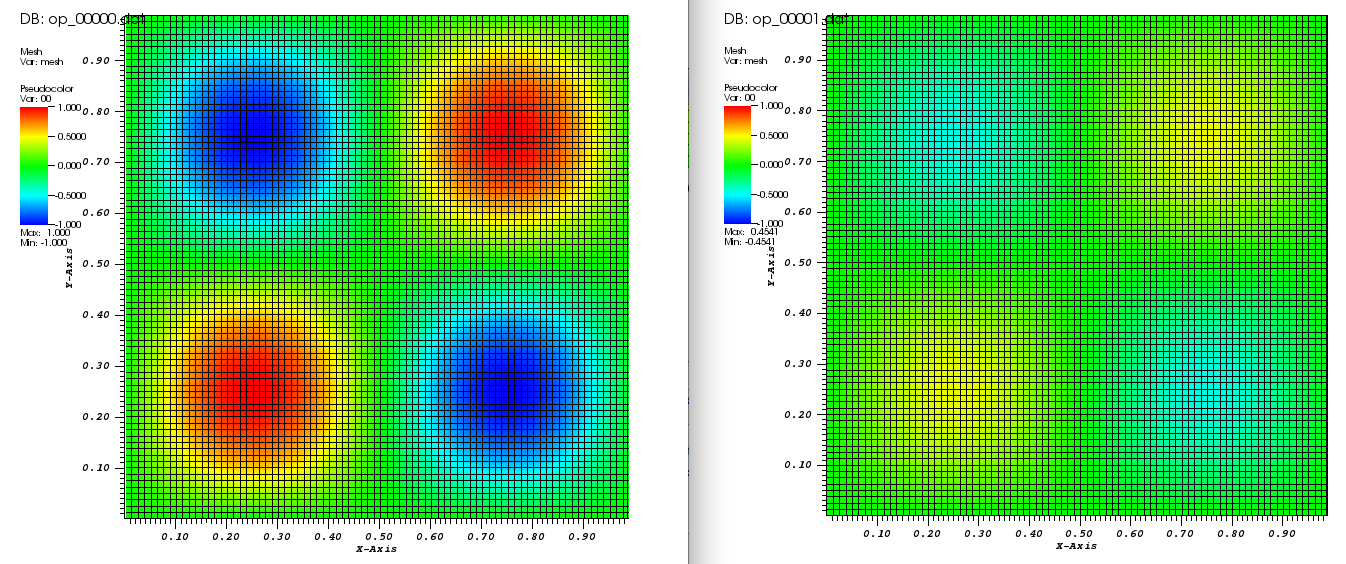
Initial solution: \(u\left(x,y,0\right) = u_0\left(x,y\right)= \sin\left(2\pi x\right)\sin\left(2\pi y\right)\)
Exact solution: \(u\left(x,y,t\right) = \exp\left[-\pi^2 \left(4\nu_x + 4\nu_y\right) t\right] u0\left(x,y\right)\).

Numerical Method:

Spatial discretization (parabolic): 2nd order (Interp2PrimSecondOrder()), conservative (ParabolicFunctionCons1Stage())
Time integration: PETSc (SolvePETSc())
- Method Class: Additive Runge-Kutta method (TSARKIMEX - https://petsc.org/release/docs/manualpages/TS/TSARKIMEX.html) - Although the ARK methods are semi-implicit (IMEX), here they are used in the "fully implicit" mode, i.e., the implicit method is used to solve the complete equation (Note the flag -ts_arkimex_fully_implicit in .petscrc).
- Specific method: Kennedy-Carpenter ARK4 (TSARKIMEX4 - https://petsc.org/release/docs/manualpages/TS/TSARKIMEX4.html)

Input files required:

.petscrc

# See PETSc documentation for more details (https://petsc.org/release/overview/).
# Note that if the following are specified in this file, the corresponding inputs in solver.inp are *ignored*.
# + "-ts_dt" (time step size): ignores "dt" in solver.inp
# + "-ts_max_steps" (maximum number of time iterations): ignores "n_iter" in solver.inp
# + "-ts_max_time" (final simulation time): ignores "n_iter" X "dt" in solver.inp
# Use PETSc time-integration
-use-petscts
# Final time
-ts_max_time 10.0
# Time step size
-ts_dt 1.0
# Maximum number of iterations
-ts_max_steps 10
# Time integration scheme type - ARK
-ts_type arkimex
-ts_arkimex_type 4
-ts_arkimex_fully_implicit
# Print time step information to screen
-ts_monitor
# Local truncation error-based time-step adaptivity
-ts_adapt_type basic
# Print time step adaptivity info to screen
-ts_adapt_monitor
# For linear problens, tell nonlinear solver (SNES) to only use the linear solver (KSP)
-snes_type ksponly
# Print SNES iteration information to screen
-snes_monitor
# Linear solver (KSP) type
-ksp_type gmres
# Set relative tolerance
-ksp_rtol 1e-6
# Set absolute tolerance
-ksp_atol 1e-6
# Print KSP iteration information to screen
-ksp_monitor

solver.inp

begin
  ndims             2
  nvars             1
  size              80 80
  iproc             2 2
  ghost             3
  n_iter            10
  time_scheme       rk
  time_scheme_type  ssprk3
  par_space_type    nonconservative-1stage
  par_space_scheme  4
  dt                1.0
  screen_op_iter    1
  file_op_iter      99999
  op_file_format    tecplot2d
  op_overwrite      no
  model             linear-advection-diffusion-reaction
end

boundary.inp

4
periodic      0     1     0     0   -3.0    3.0
periodic      0    -1     0     0   -3.0    3.0
periodic      1     1  -6.0   6.0      0      0
periodic      1    -1  -6.0   6.0      0      0

physics.inp (specifies \(\nu_x\) and \(\nu_y\))

begin
  diffusion 0.001 0.001
end

To generate initial.inp (initial solution) and exact.inp (exact solution), compile and run the following code in the run directory.

#include <stdio.h>
#include <stdlib.h>
#include <math.h>
#include <string.h>
int main()
{
  double pi = 4.0*atan(1.0);
    int NI=100,NJ=100,ndims=1,niter=0;
  FILE *in, *out;
  double nu_x,nu_y,dt,final_time;
  char ip_file_type[50];
  strcpy(ip_file_type,"ascii");
  printf("Reading file \"solver.inp\"...\n");
  in = fopen("solver.inp","r");
  if (!in) printf("Error: Input file \"solver.inp\" not found. Default values will be used.\n");
  else {
    char word[500];
    fscanf(in,"%s",word);
    if (!strcmp(word, "begin")){
      while (strcmp(word, "end")){
        fscanf(in,"%s",word);
        if (!strcmp(word, "ndims"))     fscanf(in,"%d",&ndims);
        else if (!strcmp(word, "size")) {
          fscanf(in,"%d",&NI);
          fscanf(in,"%d",&NJ);
        } else if (!strcmp(word, "dt")) fscanf(in,"%lf",&dt);
        else if (!strcmp(word, "n_iter")) fscanf(in,"%d",&niter);
        else if (!strcmp(word, "ip_file_type")) fscanf(in,"%s",ip_file_type);
      }
    } else printf("Error: Illegal format in solver.inp. Crash and burn!\n");
  }
  fclose(in);
  if (ndims != 2) {
    printf("ndims is not 2 in solver.inp. this code is to generate 2D initial conditions\n");
    return(0);
  }
    printf("Grid:\t\t\t%d X %d\n",NI,NJ);
  final_time = (double)niter * dt;
    printf("Final Time:\t\t\t%lf\n",final_time);
  printf("Reading file \"physics.inp\"...\n");
  in = fopen("physics.inp","r");
  if (!in) {
    printf("Error: Input file \"physics.inp\" not found. Default values will be used.\n");
    nu_x = nu_y = 1.0;
  } else {
    char word[500];
    fscanf(in,"%s",word);
    if (!strcmp(word, "begin")){
      while (strcmp(word, "end")){
        fscanf(in,"%s",word);
        if (!strcmp(word,"diffusion")) {
          fscanf(in,"%lf",&nu_x);
          fscanf(in,"%lf",&nu_y);
        }
      }
    } else printf("Error: Illegal format in solver.inp. Crash and burn!\n");
  }
  fclose(in);
    printf("Diffusion Coeff:\t\t\t%lf, %lf\n",nu_x,nu_y);
    int i,j;
    double dx = 1.0 / ((double)NI);
    double dy = 1.0 / ((double)NJ);
    double *x, *y, *u;
    x = (double*) calloc (NI   , sizeof(double));
    y = (double*) calloc (NJ   , sizeof(double));
    u = (double*) calloc (NI*NJ, sizeof(double));
  /* set grid */
    for (i = 0; i < NI; i++){
    for (j = 0; j < NJ; j++){
        x[i] = i*dx;
        y[j] = j*dy;
      }
    }
  /* initial solution */
    for (i = 0; i < NI; i++){
    for (j = 0; j < NJ; j++){
      int p = NJ*i + j;
          u[p] = sin(2*pi*x[i]) * sin(2*pi*y[j]);
      }
    }
  if (!strcmp(ip_file_type,"ascii")) {
    printf("Writing ASCII file initial.inp.\n");
      out = fopen("initial.inp","w");
    for (i = 0; i < NI; i++)  fprintf(out,"%lf ",x[i]);
    fprintf(out,"\n");
    for (j = 0; j < NJ; j++)  fprintf(out,"%lf ",y[j]);
    fprintf(out,"\n");
    for (j = 0; j < NJ; j++)    {
        for (i = 0; i < NI; i++)    {
        int p = NJ*i + j;
        fprintf(out,"%lf ",u[p]);
      }
    }
    fprintf(out,"\n");
      fclose(out);
  } else if ((!strcmp(ip_file_type,"binary")) || (!strcmp(ip_file_type,"bin"))) {
    printf("Error: Writing binary initial solution file not implemented. ");
    printf("Please choose ip_file_type in solver.inp as \"ascii\".\n");
  }
  /* exact solution */
    for (i = 0; i < NI; i++){
    for (j = 0; j < NJ; j++){
      int p = NJ*i + j;
          u[p] = exp(-pi*pi*(4*nu_x+4*nu_y)*final_time) * sin(2*pi*x[i]) * sin(2*pi*y[j]);
      }
    }
  if (!strcmp(ip_file_type,"ascii")) {
    printf("Writing ASCII file exact.inp.\n");
      out = fopen("exact.inp","w");
    for (i = 0; i < NI; i++)  fprintf(out,"%lf ",x[i]);
    fprintf(out,"\n");
    for (j = 0; j < NJ; j++)  fprintf(out,"%lf ",y[j]);
    fprintf(out,"\n");
    for (j = 0; j < NJ; j++)    {
        for (i = 0; i < NI; i++)    {
        int p = NJ*i + j;
        fprintf(out,"%lf ",u[p]);
      }
    }
    fprintf(out,"\n");
      fclose(out);
  } else if ((!strcmp(ip_file_type,"binary")) || (!strcmp(ip_file_type,"bin"))) {
    printf("Error: Writing binary exact solution file not implemented. ");
    printf("Please choose ip_file_type in solver.inp as \"ascii\".\n");
  }
    free(x);
    free(y);
    free(u);
    return(0);
}

Output:

Note that iproc is set to

2 2

in solver.inp (i.e., 2 processors along x, and 2 processors along y). Thus, this example should be run with 4 MPI ranks (or change iproc).

After running the code, there should be 2 output files: op_00000.dat (initial solution at t=0) and op_00001.dat (final solution at t=10). Since HyPar::op_overwrite is set to no in solver.inp, separate files are written for solutions at each output time.

HyPar::op_file_format is set to tecplot2d in solver.inp, and thus, all the files are in a format that Tecplot (http://www.tecplot.com/) or other visualization software supporting the Tecplot format (e.g. VisIt - https://wci.llnl.gov/simulation/computer-codes/visit/) can read. In these files, the first two lines are the Tecplot headers, after which the data is written out as: the first two columns are grid indices, the next two columns are x and y coordinates, and the final column is the solution. HyPar::op_file_format can be set to text to get the solution files in plain text format (which can be read in and visualized in MATLAB for example).

The following plots show the initial and final solutions:

Since the exact solution is available at the final time , the numerical errors are calculated and reported on screen (see below) as well as errors.dat:

80 80 2 2 1.0000000000000000E+00 9.0418545289592411E-05 9.0523947323434799E-05 9.0376457451387957E-05 6.7724700000000004E-01 6.8291199999999996E-01

The numbers are: number of grid points in each dimension (HyPar::dim_global), number of processors in each dimension (MPIVariables::iproc), time step size (HyPar::dt), L1, L2, and L-infinity errors (HyPar::error), solver wall time (seconds) (i.e., not accounting for initialization, and cleaning up), and total wall time.

Expected screen output:

HyPar - Parallel (MPI) version with 4 processes
Compiled with PETSc time integration.
Reading solver inputs from file "solver.inp".
    No. of dimensions                          : 2
    No. of variables                           : 1
    Domain size                                : 80 80 
    Processes along each dimension             : 2 2 
    No. of ghosts pts                          : 3
    No. of iter.                               : 10
    Restart iteration                          : 0
    Time integration scheme                    : PETSc 
    Spatial discretization scheme (hyperbolic) : 1
    Split hyperbolic flux term?                : no
    Interpolation type for hyperbolic term     : characteristic
    Spatial discretization type   (parabolic ) : nonconservative-1stage
    Spatial discretization scheme (parabolic ) : 4
    Time Step                                  : 1.000000E+00
    Check for conservation                     : no
    Screen output iterations                   : 1
    File output iterations                     : 99999
    Initial solution file type                 : ascii
    Initial solution read mode                 : serial
    Solution file write mode                   : serial
    Solution file format                       : tecplot2d
    Overwrite solution file                    : no
    Physical model                             : linear-advection-diffusion-reaction
Partitioning domain.
Allocating data arrays.
Reading array from ASCII file initial.inp (Serial mode).
Volume integral of the initial solution:
 6.9388939039072284E-17
Reading boundary conditions from "boundary.inp".
  Boundary                       periodic:  Along dimension  0 and face +1
  Boundary                       periodic:  Along dimension  0 and face -1
  Boundary                       periodic:  Along dimension  1 and face +1
  Boundary                       periodic:  Along dimension  1 and face -1
boundary condition(s) read.
Initializing solvers.
Initializing physics. Model = "linear-advection-diffusion-reaction"
Reading physical model inputs from file "physics.inp".
Setting up PETSc time integration... 
Implicit-Explicit time-integration:-
Hyperbolic        term: Explicit
Parabolic         term: Implicit
Source            term: Implicit
SolvePETSc(): Problem type is linear.
** Starting PETSc time integration **
TS dt 1. time 0.
Writing solution file op_00000.dat.
SNES Function norm 6.316544587530e+00 
KSP Residual norm 6.316544587530e+00 
KSP Residual norm 1.957710244371e-02 
KSP Residual norm 3.361519708928e-03 
KSP Residual norm 9.036909021230e-04 
KSP Residual norm 3.013121611804e-04 
KSP Residual norm 1.137242880954e-04 
KSP Residual norm 5.178226136166e-05 
KSP Residual norm 2.570197965195e-05 
KSP Residual norm 1.316528862842e-05 
KSP Residual norm 7.601607049462e-06 
KSP Residual norm 3.908442252440e-06 
SNES Function norm 3.908442250249e-06 
SNES Function norm 2.095079996653e+00 
KSP Residual norm 2.095079996653e+00 
KSP Residual norm 2.510344078062e-03 
KSP Residual norm 4.567813299765e-04 
KSP Residual norm 1.272576137252e-04 
KSP Residual norm 4.461493869201e-05 
KSP Residual norm 1.811026261651e-05 
KSP Residual norm 8.915721814240e-06 
KSP Residual norm 4.913216367368e-06 
KSP Residual norm 2.664096961097e-06 
KSP Residual norm 1.502540792653e-06 
SNES Function norm 1.502540795606e-06 
SNES Function norm 3.573714118015e+00 
KSP Residual norm 3.573714118015e+00 
KSP Residual norm 5.053890716060e-03 
KSP Residual norm 7.320195789742e-04 
KSP Residual norm 1.744389523801e-04 
KSP Residual norm 4.950310784859e-05 
KSP Residual norm 1.522546617408e-05 
KSP Residual norm 7.002876956220e-06 
KSP Residual norm 3.999190747677e-06 
KSP Residual norm 2.399450364472e-06 
SNES Function norm 2.399450367203e-06 
SNES Function norm 2.796553133414e+00 
KSP Residual norm 2.796553133414e+00 
KSP Residual norm 2.038620931170e-04 
KSP Residual norm 2.124492063383e-05 
KSP Residual norm 8.324415828222e-06 
KSP Residual norm 2.704220911566e-06 
SNES Function norm 2.704220925206e-06 
SNES Function norm 1.795270247389e+00 
KSP Residual norm 1.795270247389e+00 
KSP Residual norm 2.923950492658e-03 
KSP Residual norm 5.761824076292e-04 
KSP Residual norm 1.603745824616e-04 
KSP Residual norm 5.503478416224e-05 
KSP Residual norm 2.129684291986e-05 
KSP Residual norm 9.101849874831e-06 
KSP Residual norm 4.205090333701e-06 
KSP Residual norm 1.935475804159e-06 
KSP Residual norm 1.067584928673e-06 
SNES Function norm 1.067584944838e-06 
      TSAdapt 'basic': step   0 accepted t=0          + 1.000e+00 wlte=0.000157 family='arkimex' scheme=0:'4' dt=8.036e+00 
Iteration:      1  Time: 1.000E+00  Max CFL: 0.000E+00  Max Diff. No.: 5.143E+01  
TS dt 8.03591 time 1.
SNES Function norm 5.836991369676e+00 
KSP Residual norm 5.836991369676e+00 
KSP Residual norm 1.606571105711e-02 
KSP Residual norm 3.555429854438e-03 
KSP Residual norm 1.054145874303e-03 
KSP Residual norm 3.816560275222e-04 
KSP Residual norm 1.553148138111e-04 
KSP Residual norm 7.141447707860e-05 
KSP Residual norm 3.573885486615e-05 
KSP Residual norm 1.762311481526e-05 
KSP Residual norm 1.102632790155e-05 
KSP Residual norm 7.604890134366e-06 
KSP Residual norm 5.891062368248e-06 
KSP Residual norm 4.706157846087e-06 
SNES Function norm 4.706157830647e-06 
SNES Function norm 1.782942356388e+00 
KSP Residual norm 1.782942356388e+00 
KSP Residual norm 1.853260541300e-03 
KSP Residual norm 4.152156454596e-04 
KSP Residual norm 1.249350988068e-04 
KSP Residual norm 4.696061156813e-05 
KSP Residual norm 2.117380251812e-05 
KSP Residual norm 1.205120355741e-05 
KSP Residual norm 9.368337382944e-06 
KSP Residual norm 7.891654819102e-06 
KSP Residual norm 6.510195954867e-06 
KSP Residual norm 4.790589179572e-06 
KSP Residual norm 3.425898719082e-06 
KSP Residual norm 2.475991492431e-06 
KSP Residual norm 1.703848519171e-06 
SNES Function norm 1.703848525017e-06 
SNES Function norm 2.902135807469e+00 
KSP Residual norm 2.902135807469e+00 
KSP Residual norm 5.342770595234e-03 
KSP Residual norm 1.158645143640e-03 
KSP Residual norm 3.390080212082e-04 
KSP Residual norm 1.204503860550e-04 
KSP Residual norm 4.763446757099e-05 
KSP Residual norm 2.184096593991e-05 
KSP Residual norm 1.130727398036e-05 
KSP Residual norm 5.861271256970e-06 
KSP Residual norm 3.630792677972e-06 
KSP Residual norm 2.222925203565e-06 
SNES Function norm 2.222925226704e-06 
SNES Function norm 1.980333066245e+00 
KSP Residual norm 1.980333066245e+00 
KSP Residual norm 5.226840000371e-04 
KSP Residual norm 1.093141094418e-04 
KSP Residual norm 3.323418670939e-05 
KSP Residual norm 1.422858125667e-05 
KSP Residual norm 8.078849683438e-06 
KSP Residual norm 5.778091707955e-06 
KSP Residual norm 3.508662934946e-06 
KSP Residual norm 1.735392017695e-06 
SNES Function norm 1.735392015197e-06 
SNES Function norm 1.077300487771e+00 
KSP Residual norm 1.077300487771e+00 
KSP Residual norm 1.456726027125e-03 
KSP Residual norm 3.455843454324e-04 
KSP Residual norm 1.061231373462e-04 
KSP Residual norm 4.008293887161e-05 
KSP Residual norm 1.952757666668e-05 
KSP Residual norm 1.109244240131e-05 
KSP Residual norm 7.356562327907e-06 
KSP Residual norm 5.288314779945e-06 
KSP Residual norm 4.036767337599e-06 
KSP Residual norm 2.947354553864e-06 
KSP Residual norm 2.308355431743e-06 
KSP Residual norm 1.918350363886e-06 
KSP Residual norm 1.521771393111e-06 
KSP Residual norm 1.098473343667e-06 
KSP Residual norm 6.509223678076e-07 
SNES Function norm 6.509223650753e-07 
      TSAdapt 'basic': step   1 accepted t=1          + 8.036e+00 wlte=0.0845 family='arkimex' scheme=0:'4' dt=9.641e-01 
Iteration:      2  Time: 9.036E+00  Max CFL: 0.000E+00  Max Diff. No.: 6.170E+00  
TS dt 0.964091 time 9.03591
SNES Function norm 3.095086711822e+00 
KSP Residual norm 3.095086711822e+00 
KSP Residual norm 5.091402309070e-05 
KSP Residual norm 1.503364447884e-05 
KSP Residual norm 4.877560179260e-06 
KSP Residual norm 2.080593258447e-06 
SNES Function norm 2.080593257754e-06 
SNES Function norm 1.027053563489e+00 
KSP Residual norm 1.027053563489e+00 
KSP Residual norm 1.637020708637e-05 
KSP Residual norm 4.901437619396e-06 
KSP Residual norm 2.425813232555e-06 
KSP Residual norm 1.109960615936e-06 
KSP Residual norm 5.608757075441e-07 
SNES Function norm 5.608757095682e-07 
SNES Function norm 1.752240074891e+00 
KSP Residual norm 1.752240074891e+00 
KSP Residual norm 1.244726995357e-05 
KSP Residual norm 3.142472564310e-06 
KSP Residual norm 8.965080697849e-07 
SNES Function norm 8.965080704085e-07 
SNES Function norm 1.372183949527e+00 
KSP Residual norm 1.372183949527e+00 
KSP Residual norm 7.864867112361e-06 
KSP Residual norm 1.748857757569e-06 
KSP Residual norm 7.155189740006e-07 
SNES Function norm 7.155189732236e-07 
SNES Function norm 8.814088207223e-01 
KSP Residual norm 8.814088207223e-01 
KSP Residual norm 1.449905447682e-05 
KSP Residual norm 5.448657008534e-06 
KSP Residual norm 1.971204312598e-06 
KSP Residual norm 1.056736099819e-06 
KSP Residual norm 6.128162078077e-07 
SNES Function norm 6.128162098664e-07 
      TSAdapt 'basic': step   2 accepted t=9.03591    + 9.641e-01 wlte=1.34e-05 family='arkimex' scheme=0:'4' dt=9.641e+00 
Iteration:      3  Time: 1.000E+01  Max CFL: 0.000E+00  Max Diff. No.: 6.170E+01  
TS dt 9.64091 time 10.
** Completed PETSc time integration **
Writing solution file op_00001.dat.
Reading array from ASCII file exact.inp (Serial mode).
Computed errors:
  L1         Error           : 9.0418545289592411E-05
  L2         Error           : 9.0523947323434799E-05
  Linfinity  Error           : 9.0376457451387957E-05
Conservation Errors:
0000000000000000E+00
Solver runtime (in seconds): 6.7724700000000004E-01
Total  runtime (in seconds): 6.8291199999999996E-01
Deallocating arrays.
Finished.