2D Euler Equations (with gravitational force) - Rising Thermal Bubble
Location: hypar/Examples/2D/NavierStokes2D/RisingThermalBubble_PETSc_IMEX (This directory contains all the input files needed to run this case. If there is a Run.m, run it in MATLAB to quickly set up, run, and visualize the example).
Governing equations: 2D Euler Equations (navierstokes2d.h - By default, NavierStokes2D::Re is set to -1 which makes the code skip the parabolic terms, i.e., the 2D Euler equations are solved.)
Reference:
- Giraldo, F.X., Restelli, M., "A study of spectral element and discontinuous Galerkin methods for the Navier–Stokes equations in nonhydrostatic mesoscale atmospheric modeling: Equation sets and test cases", J. Comput. Phys., 227, 2008, 3849–3877, (Section 3.2).
The problem is solved here using implicit-explicit (IMEX) time integration, where the hyperbolic flux is partitioned into its entropy and acoustic components with the former integrated explicitly and the latter integrated implicitly. See the following reference:
- Ghosh, D., Constantinescu, E. M., "Semi-Implicit Time Integration of Atmospheric Flows with Characteristic-Based Flux Partitioning", SIAM Journal on Scientific Computing, 38 (3), 2016, A1848-A1875, http://dx.doi.org/10.1137/15M1044369.
Domain: \(0 \le x,y \le 1000\,m\), "slip-wall" (_SLIP_WALL_) boundary conditions on all sides.
Initial solution: See references above.
Other parameters (all dimensional quantities are in SI units):
- Specific heat ratio \(\gamma = 1.4\) (NavierStokes2D::gamma)
- Universal gas constant \(R = 287.058\) (NavierStokes2D::R)
- Gravitational force per unit mass \(g = 9.8\) along y-axis (NavierStokes2D::grav_y)
- Reference density (at zero altitude) \(\rho_{ref} = 1.1612055171196529\) (NavierStokes2D::rho0)
- Reference pressure (at zero altitude) \(P_{ref} = 100000\) (NavierStokes2D::p0)
- Hydrostatic balance type 2 (NavierStokes2D::HB)
Numerical method:
- Spatial discretization (hyperbolic): 5th order WENO (Interp1PrimFifthOrderWENO())
- Time integration: PETSc (SolvePETSc())
- Method Class: Additive Runge-Kutta method (TSARKIMEX - https://petsc.org/release/docs/manualpages/TS/TSARKIMEX.html)
- Specific method: Kennedy-Carpenter ARK4 (TSARKIMEX4 - https://petsc.org/release/docs/manualpages/TS/TSARKIMEX4.html)
Input files required:
.petscrc
# See PETSc documentation for more details (https://petsc.org/release/overview/).
# Note that if the following are specified in this file, the corresponding inputs in solver.inp are *ignored*.
# + "-ts_dt" (time step size): ignores "dt" in solver.inp
# + "-ts_max_steps" (maximum number of time iterations): ignores "n_iter" in solver.inp
# + "-ts_max_time" (final simulation time): ignores "n_iter" X "dt" in solver.inp
# Use PETSc time-integration
-use-petscts
# Final time
-ts_max_time 200.0
# Time step size
-ts_dt 0.2
# Maximum number of iterations
-ts_max_steps 1000000
# Time integration scheme type - ARK
-ts_type arkimex
-ts_arkimex_type 4
# Specify the terms to treat explicitly and implicitly
# In this example, the hyperbolic flux is partitioned
# into its entropy and acoustic components: f = [f-df] + [df]
# [f-df] - entropy component
# [df] - acoustic component
-hyperbolic_f_explicit # treat [f-df] explicitly
-hyperbolic_df_implicit # treat [df] implicitly
-source_implicit # treat source term implicitly
# thus, time step size is limited by the [f-df] term, i.e.,
# the flow velocity.
# print time step info to screen
-ts_monitor
# local truncation error based time-step adaptivity
-ts_adapt_type basic
# print time-step adaptivity info to screen
-ts_adapt_monitor
# For linear problens, tell nonlinear solver (SNES) to only use the linear solver (KSP)
-snes_type ksponly
# Linear solver (KSP) type
-ksp_type gmres
# Set relative tolerance
-ksp_rtol 1e-6
# Set absolute tolerance
-ksp_atol 1e-6
# use a preconditioner for solving the system
-with_pc
# preconditioner type - block Jacobi
-pc_type bjacobi
# apply right preconditioner
-ksp_pc_side RIGHT
solver.inp
begin
ndims 2
nvars 4
size 101 101
iproc 1 1
ghost 3
n_iter 1000
restart_iter 0
time_scheme rk
time_scheme_type ssprk3
hyp_space_scheme weno5
hyp_flux_split yes
hyp_interp_type components
par_space_type nonconservative-2stage
par_space_scheme 4
dt 0.2
conservation_check no
screen_op_iter 1
file_op_iter 99999
input_mode serial
ip_file_type binary
output_mode serial
op_file_format binary
op_overwrite yes
model navierstokes2d
end
boundary.inp
4
slip-wall 0 1 0 0 0 1000.0
0.0 0.0
slip-wall 0 -1 0 0 0 1000.0
0.0 0.0
slip-wall 1 1 0 1000.0 0 0
0.0 0.0
slip-wall 1 -1 0 1000.0 0 0
0.0 0.0
physics.inp
begin
gamma 1.4
upwinding rusanov
gravity 0.0 9.8
rho_ref 1.1612055171196529
p_ref 100000.0
R 287.058
HB 2
end
weno.inp (optional)
begin
mapped 0
borges 0
yc 0
no_limiting 1
epsilon 0.000001
p 2.0
rc 0.3
xi 0.001
end
To generate initial.inp (initial solution), compile and run the following code in the run directory.
#include <stdio.h>
#include <stdlib.h>
#include <math.h>
#include <string.h>
{
return(exp(a*log(x)));
}
int main()
{
double gamma = 1.4;
double R = 287.058;
double rho_ref = 1.1612055171196529;
double p_ref = 100000.0;
double grav_x = 0.0;
double grav_y = 9.8;
int HB = 0;
int NI,NJ,ndims;
char ip_file_type[50]; strcpy(ip_file_type,"ascii");
FILE *in;
printf("Reading file \"solver.inp\"...\n");
in = fopen("solver.inp","r");
if (!in) {
printf("Error: Input file \"solver.inp\" not found.\n");
return(0);
} else {
char word[500];
fscanf(in,"%s",word);
if (!strcmp(word, "begin")) {
while (strcmp(word, "end")) {
fscanf(in,"%s",word);
if (!strcmp(word, "ndims")) fscanf(in,"%d",&ndims);
else if (!strcmp(word, "size")) {
fscanf(in,"%d",&NI);
fscanf(in,"%d",&NJ);
} else if (!strcmp(word, "ip_file_type")) fscanf(in,"%s",ip_file_type);
}
} else printf("Error: Illegal format in solver.inp. Crash and burn!\n");
}
fclose(in);
printf("Reading file \"physics.inp\"...\n");
in = fopen("physics.inp","r");
if (!in) {
printf("Error: Input file \"physics.inp\" not found.\n");
return(0);
} else {
char word[500];
fscanf(in,"%s",word);
if (!strcmp(word, "begin")) {
while (strcmp(word, "end")) {
fscanf(in,"%s",word);
if (!strcmp(word, "rho_ref")) fscanf(in,"%lf",&rho_ref);
else if (!strcmp(word, "p_ref" )) fscanf(in,"%lf",&p_ref );
else if (!strcmp(word, "gamma" )) fscanf(in,"%lf",&gamma );
else if (!strcmp(word, "R" )) fscanf(in,"%lf",&R );
else if (!strcmp(word, "HB" )) fscanf(in,"%d" ,&HB );
else if (!strcmp(word, "gravity")) {
fscanf(in,"%lf",&grav_x );
fscanf(in,"%lf",&grav_y );
}
}
} else printf("Error: Illegal format in physics.inp. Crash and burn!\n");
}
fclose(in);
if (ndims != 2) {
printf("ndims is not 2 in solver.inp. this code is to generate 2D initial conditions\n");
return(0);
}
if (HB != 2) {
printf("Error: Specify \"HB\" as 2 in physics.inp.\n");
}
printf("Grid:\t\t\t%d X %d\n",NI,NJ);
printf("Reference density and pressure: %lf, %lf.\n",rho_ref,p_ref);
int i,j;
double dx = 1000.0 / ((double)(NI-1));
double dy = 1000.0 / ((double)(NJ-1));
double *x, *y, *u0, *u1, *u2, *u3;
x = (double*) calloc (NI , sizeof(double));
y = (double*) calloc (NJ , sizeof(double));
u0 = (double*) calloc (NI*NJ, sizeof(double));
u1 = (double*) calloc (NI*NJ, sizeof(double));
u2 = (double*) calloc (NI*NJ, sizeof(double));
u3 = (double*) calloc (NI*NJ, sizeof(double));
/* Initial perturbation center */
double xc = 500;
double yc = 350;
double Cp = gamma * R / (gamma-1.0);
/* initial perturbation parameters */
double tc = 0.5;
double pi = 4.0*atan(1.0);
double rc = 250.0;
double T_ref = p_ref / (R * rho_ref);
for (i = 0; i < NI; i++){
for (j = 0; j < NJ; j++){
x[i] = i*dx;
y[j] = j*dy;
int p = NJ*i + j;
/* temperature peturbation */
double r = sqrt((x[i]-xc)*(x[i]-xc)+(y[j]-yc)*(y[j]-yc));
double dtheta = (r>rc ? 0.0 : (0.5*tc*(1.0+cos(pi*r/rc))) );
double theta = T_ref + dtheta;
double Pexner = 1.0 - (grav_y*y[j])/(Cp*T_ref);
double rho = (p_ref/(R*theta)) * raiseto(Pexner, (1.0/(gamma-1.0)));
double E = rho * (R/(gamma-1.0)) * theta*Pexner;
u0[p] = rho;
u1[p] = 0.0;
u2[p] = 0.0;
u3[p] = E;
}
}
FILE *out;
if (!strcmp(ip_file_type,"ascii")) {
printf("Writing ASCII initial solution file initial.inp\n");
out = fopen("initial.inp","w");
for (i = 0; i < NI; i++) fprintf(out,"%lf ",x[i]);
fprintf(out,"\n");
for (j = 0; j < NJ; j++) fprintf(out,"%lf ",y[j]);
fprintf(out,"\n");
for (j = 0; j < NJ; j++) {
for (i = 0; i < NI; i++) {
int p = NJ*i + j;
fprintf(out,"%lf ",u0[p]);
}
}
fprintf(out,"\n");
for (j = 0; j < NJ; j++) {
for (i = 0; i < NI; i++) {
int p = NJ*i + j;
fprintf(out,"%lf ",u1[p]);
}
}
fprintf(out,"\n");
for (j = 0; j < NJ; j++) {
for (i = 0; i < NI; i++) {
int p = NJ*i + j;
fprintf(out,"%lf ",u2[p]);
}
}
fprintf(out,"\n");
for (j = 0; j < NJ; j++) {
for (i = 0; i < NI; i++) {
int p = NJ*i + j;
fprintf(out,"%lf ",u3[p]);
}
}
fprintf(out,"\n");
fclose(out);
} else if ((!strcmp(ip_file_type,"binary")) || (!strcmp(ip_file_type,"bin"))) {
printf("Writing binary initial solution file initial.inp\n");
out = fopen("initial.inp","wb");
fwrite(x,sizeof(double),NI,out);
fwrite(y,sizeof(double),NJ,out);
double *U = (double*) calloc (4*NI*NJ,sizeof(double));
for (i=0; i < NI; i++) {
for (j = 0; j < NJ; j++) {
int p = NJ*i + j;
int q = NI*j + i;
U[4*q+0] = u0[p];
U[4*q+1] = u1[p];
U[4*q+2] = u2[p];
U[4*q+3] = u3[p];
}
}
fwrite(U,sizeof(double),4*NI*NJ,out);
free(U);
fclose(out);
}
free(x);
free(y);
free(u0);
free(u1);
free(u2);
free(u3);
return(0);
}
Output:
Note that iproc is set to
1 1
in solver.inp (i.e., 1 processor along x, and 1 processor along y). Thus, this example should be run with 1 MPI rank (or change iproc).
After running the code, there should be a output file op.bin (final solution),
since HyPar::op_overwrite is set to yes in solver.inp.
HyPar::op_file_format is set to binary in solver.inp, and thus, the file is written out in the binary format, see WriteBinary(). The binary file contains the conserved variables \(\left(\rho, \rho u, \rho v, e\right)\). The following code converts these variables to the primitive variables of interest to atmospheric flows \(\left(\rho, u, v, p, \theta\right)\). It also writes out the hydrostatically balanced quantities \(\left(\rho_0,\pi_0, \theta_0\right)\) for this case that can be used to compute and plot the temperature and density perturbations. These variables are then written to either a tecplot2d or text file. (compile and run it in the run directory):
/*
Rising Thermal Bubble:-
The code takes a binary solution file (that contains the
conserved variable (rho, rho*u, rho*v, e) as its input
and calculates the primitive atmospheric flow variables:
rho, u, v, P, theta, pi, rho0, P0, theta0, pi0
and writes them to a tecplot file.
*/
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#include <math.h>
typedef struct _parameters_{
double grav_x, grav_y, R, gamma, P_ref, rho_ref;
int HB;
} Parameters;
void IncrementFilename(char *f)
{
if (f[7] == '9') {
f[7] = '0';
if (f[6] == '9') {
f[6] = '0';
if (f[5] == '9') {
f[5] = '0';
if (f[4] == '9') {
f[4] = '0';
if (f[3] == '9') {
f[3] = '0';
fprintf(stderr,"Warning: file increment hit max limit. Resetting to zero.\n");
} else {
f[3]++;
}
} else {
f[4]++;
}
} else {
f[5]++;
}
} else {
f[6]++;
}
} else {
f[7]++;
}
}
{
return(exp(a*log(x)));
}
{
printf("\tWriting tecplot solution file %s.\n",f);
FILE *out;
out = fopen(f,"w");
if (!out) {
fprintf(stderr,"Error: could not open %s for writing.\n",f);
return;
}
double *X = x;
double *Y = x+imax;
/* writing tecplot data file headers */
fprintf(out,"VARIABLES=\"I\",\"J\",\"X\",\"Y\",");
fprintf(out,"\"RHO\",\"U\",\"V\",\"P\",");
fprintf(out,"\"THETA\",\"RHO0\",\"P0\",");
fprintf(out,"\"PI0\",\"THETA0\",\n");
fprintf(out,"ZONE I=%d,J=%d,F=POINT\n",imax,jmax);
/* writing the data */
int i,j;
for (j=0; j<jmax; j++) {
for (i=0; i<imax; i++) {
int v, p = i + imax*j;
fprintf(out,"%4d %4d ",i,j);
fprintf(out,"%1.16E %1.16E ",X[i],Y[j]);
for (v=0; v<nvars; v++) fprintf(out,"%1.16E ",u[nvars*p+v]);
fprintf(out,"\n");
}
}
fclose(out);
return;
}
void WriteText2D(int nvars,int imax, int jmax,double *x,double *u,char *f)
{
printf("\tWriting text solution file %s.\n",f);
FILE *out;
out = fopen(f,"w");
if (!out) {
fprintf(stderr,"Error: could not open %s for writing.\n",f);
return;
}
double *X = x;
double *Y = x+imax;
/* writing the data */
int i,j;
for (j=0; j<jmax; j++) {
for (i=0; i<imax; i++) {
int v, p = i + imax*j;
fprintf(out,"%4d %4d ",i,j);
fprintf(out,"%1.16E %1.16E ",X[i],Y[j]);
for (v=0; v<nvars; v++) fprintf(out,"%1.16E ",u[nvars*p+v]);
fprintf(out,"\n");
}
}
fclose(out);
return;
}
int PostProcess(char *fname, char *oname, void *p, int flag)
{
Parameters *params = (Parameters*) p;
FILE *in; in = fopen(fname,"rb");
if (!in) return(-1);
printf("Reading file %s.\n",fname);
int ndims, nvars;
double *U,*x;
/* read the file headers */
fread(&ndims,sizeof(int),1,in);
fread(&nvars,sizeof(int),1,in);
/* some checks */
if (ndims != 2) {
printf("Error: ndims in %s not equal to 2!\n",fname);
return(1);
}
if (nvars != 4) {
printf("Error: nvars in %s not equal to 4!\n",fname);
return(1);
}
/* read dimensions */
int dims[ndims];
fread(dims,sizeof(int),ndims,in);
printf("Dimensions: %d x %d\n",dims[0],dims[1]);
printf("Nvars : %d\n",nvars);
/* allocate grid and solution arrays */
x = (double*) calloc (dims[0]+dims[1] ,sizeof(double));
U = (double*) calloc (dims[0]*dims[1]*nvars ,sizeof(double));
/* read grid and solution */
fread(x,sizeof(double),dims[0]+dims[1] ,in);
fread(U,sizeof(double),dims[0]*dims[1]*nvars,in);
/* done reading */
fclose(in);
int imax = dims[0];
int jmax = dims[1];
/* allocate primitive variable array (rho, u, v, P, theta, rho0, P0, pi0, theta0) */
int evars = 5;
double *Q = (double*) calloc ((nvars+evars)*imax*jmax,sizeof(double));
/* calculate primitive variables */
int i, j;
double *X = x;
double *Y = x+imax;
double grav_y = params->grav_y;
double R = params->R;
double gamma = params->gamma;
double P_ref = params->P_ref;
double rho_ref = params->rho_ref;
double T_ref = P_ref / (R*rho_ref);
double inv_gamma_m1 = 1.0 / (gamma-1.0);
double Cp = gamma * inv_gamma_m1 * R;
for (i=0; i<imax; i++) {
for (j=0; j<jmax; j++) {
int p = i + imax*j;
double rho0, theta0, Pexner, P0;
theta0 = T_ref;
Pexner = 1.0 - (grav_y*Y[j])/(Cp*T_ref);
rho0 = (P_ref/(R*theta0)) * raiseto(Pexner, inv_gamma_m1);
P0 = P_ref * raiseto(Pexner, gamma*inv_gamma_m1);
double rho, uvel, vvel, E, P, theta;
rho = U[nvars*p+0];
uvel = U[nvars*p+1] / rho;
vvel = U[nvars*p+2] / rho;
E = U[nvars*p+3];
P = (gamma-1.0) * (E - 0.5*rho*(uvel*uvel+vvel*vvel));
theta = (E-0.5*rho*(uvel*uvel+vvel*vvel))/(Pexner*rho) * ((gamma-1.0)/R);
Q[(nvars+evars)*p+0] = rho;
Q[(nvars+evars)*p+1] = uvel;
Q[(nvars+evars)*p+2] = vvel;
Q[(nvars+evars)*p+3] = P;
Q[(nvars+evars)*p+4] = theta;
Q[(nvars+evars)*p+5] = rho0;
Q[(nvars+evars)*p+6] = P0;
Q[(nvars+evars)*p+7] = Pexner;
Q[(nvars+evars)*p+8] = theta0;
}
}
/* write Tecplot/Text file */
if (flag) WriteTecplot2D(nvars+evars,imax,jmax,x,Q,oname);
else WriteText2D (nvars+evars,imax,jmax,x,Q,oname);
/* clean up */
free(U);
free(Q);
free(x);
}
int main()
{
FILE *out1, *out2, *in, *inputs;
char filename[50], op_file_format[50], tecfile[50], overwrite[50];
int flag;
printf("Write tecplot file (1) or plain text file (0): ");
scanf("%d",&flag);
if ((flag != 1) && (flag != 0)) {
printf("Error: Invalid input. Should be 1 or 0.\n");
return(0);
}
printf("Reading solver.inp.\n");
inputs = fopen("solver.inp","r");
if (!inputs) {
fprintf(stderr,"Error: File \"solver.inp\" not found.\n");
return(1);
} else {
char word[100];
fscanf(inputs,"%s",word);
if (!strcmp(word, "begin")){
while (strcmp(word, "end")){
fscanf(inputs,"%s",word);
if (!strcmp(word, "op_file_format" )) fscanf(inputs,"%s" ,op_file_format);
else if (!strcmp(word, "op_overwrite" )) fscanf(inputs,"%s" ,overwrite );
}
}
fclose(inputs);
}
if (strcmp(op_file_format,"binary") && strcmp(op_file_format,"bin")) {
printf("Error: solution output needs to be in binary files.\n");
return(0);
}
Parameters params;
/* default values */
params.grav_x = 0.0;
params.grav_y = 9.8;
params.R = 287.058;
params.gamma = 1.4;
params.P_ref = 100000.0;
params.rho_ref = 100000.0 / (params.R * 300.0);
params.HB = 0;
/* read these parameters from file */
printf("Reading physics.inp.\n");
inputs = fopen("physics.inp","r");
if (!inputs) {
fprintf(stderr,"Error: File \"physics.inp\" not found.\n");
return(1);
} else {
char word[100];
fscanf(inputs,"%s",word);
if (!strcmp(word, "begin")){
while (strcmp(word, "end")){
fscanf(inputs,"%s",word);
if (!strcmp(word, "gamma")) fscanf(inputs,"%lf",¶ms.gamma);
else if (!strcmp(word, "gravity")) {
fscanf(inputs,"%lf",¶ms.grav_x);
fscanf(inputs,"%lf",¶ms.grav_y);
} else if (!strcmp(word,"p_ref")) fscanf(inputs,"%lf",¶ms.P_ref);
else if (!strcmp(word,"rho_ref")) fscanf(inputs,"%lf",¶ms.rho_ref);
else if (!strcmp(word,"HB")) fscanf(inputs,"%d",¶ms.HB);
}
}
fclose(inputs);
}
if (params.HB != 2) {
printf("Error: \"HB\" must be specified as 2 in physics.inp.\n");
return(0);
}
if (!strcmp(overwrite,"no")) {
strcpy(filename,"op_00000.bin");
while(1) {
/* set filename */
strcpy(tecfile,filename);
tecfile[9] = 'd';
tecfile[10] = 'a';
tecfile[11] = 't';
int err = PostProcess(filename, tecfile, ¶ms, flag);
if (err == -1) {
printf("No more files found. Exiting.\n");
break;
}
IncrementFilename(filename);
}
} else if (!strcmp(overwrite,"yes")) {
strcpy(filename,"op.bin");
/* set filename */
strcpy(tecfile,filename);
tecfile[3] = 'd';
tecfile[4] = 'a';
tecfile[5] = 't';
int err = PostProcess(filename, tecfile, ¶ms, flag);
if (err == -1) {
printf("Error: op.bin not found.\n");
return(0);
}
}
return(0);
}
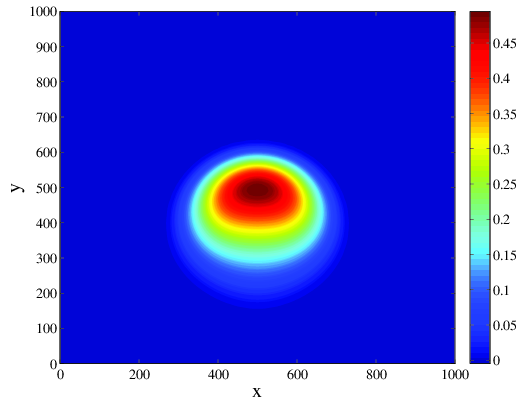
The following plot shows the potential temperature perturbation contours at the final time t=200s.
It was plotted by using the above postprocessing code to write the solution in text format and using the following MATLAB script:
% Script to plot the solution of the rising thermal bubble
% problem.
% Compile and run aux/PostProcess.c after simulation is
% completed and choose text output.
clear all;
close all;
flag = 1;
if (exist('op.dat','file'))
flag = 0;
elseif (exist('op_00000.dat','file'))
flag = 1;
else
fprintf('Error: No solution files exist.\n');
return;
end
% get physical domain dimensions from any one solution file
if (flag)
data = load('op_00000.dat');
else
data = load('op.dat');
end
imax = max(data(:,1)) + 1;
jmax = max(data(:,2)) + 1;
xcoord = reshape(data(:,3),imax,jmax);
ycoord = reshape(data(:,4),imax,jmax);
% Get screen size
scrsz = get(0,'ScreenSize');
height = 0.9 * width;
% open figure window
scrsz = get(0,'ScreenSize');
figSolution = figure('Position',[1 scrsz(4)/2 width height]);
maxfiles = 1000;
if (flag)
for n = 1:maxfiles
filename = ['op_',sprintf('%05d',n-1),'.dat'];
if (~exist(filename,'file'))
fprintf('No more files found.\n');
break;
end
fprintf('Plotting %s.\n',filename);
% read in the solution
data = load(filename);
rho = reshape(data(:, 5),imax,jmax);
uvel = reshape(data(:, 6),imax,jmax);
vvel = reshape(data(:, 7),imax,jmax);
P = reshape(data(:, 8),imax,jmax);
theta = reshape(data(:, 9),imax,jmax);
rho0 = reshape(data(:,10),imax,jmax);
P0 = reshape(data(:,11),imax,jmax);
Pexner = reshape(data(:,12),imax,jmax);
theta0 = reshape(data(:,13),imax,jmax);
% plot the solution
figure(figSolution);
handle = contourf(xcoord,ycoord,theta-theta0,'LineColor','none', ...
'LevelList',-0.05:0.005:0.5);
colorbar;
xlabel('x','FontName','Times','FontSize',20,'FontWeight','normal');
ylabel('y','FontName','Times','FontSize',20,'FontWeight','normal');
set(gca,'FontSize',14,'FontName','Times');
% write plot to files
print(figSolution,'-depsc',['Contour_',sprintf('%05d',n-1),'.eps']);
end
else
filename = 'op.dat';
if (~exist(filename,'file'))
break;
end
fprintf('Plotting %s.\n',filename);
% read in the solution
data = load(filename);
rho = reshape(data(:, 5),imax,jmax);
uvel = reshape(data(:, 6),imax,jmax);
vvel = reshape(data(:, 7),imax,jmax);
P = reshape(data(:, 8),imax,jmax);
theta = reshape(data(:, 9),imax,jmax);
rho0 = reshape(data(:,10),imax,jmax);
P0 = reshape(data(:,11),imax,jmax);
Pexner = reshape(data(:,12),imax,jmax);
theta0 = reshape(data(:,13),imax,jmax);
% plot the solution
figure(figSolution);
handle = contourf(xcoord,ycoord,theta-theta0,'LineColor','none', ...
'LevelList',-0.05:0.005:0.5);
colorbar;
xlabel('x','FontName','Times','FontSize',20,'FontWeight','normal');
ylabel('y','FontName','Times','FontSize',20,'FontWeight','normal');
set(gca,'FontSize',14,'FontName','Times');
% write plot to files
print(figSolution,'-depsc',['Contour.eps']);
end
The file function_counts.dat reports the computational expense (in terms of the number of function counts):
15
5049
0
4959
90
165
75
4794
The numbers are, respectively,
- Time iterations
- Number of times the hyperbolic term was evaluated
- Number of times the parabolic term was evaluated
- Number of times the source term was evaluated
- Number of calls to the explicit right-hand-side function (PetscRHSFunctionIMEX() or PetscRHSFunctionExpl())
- Number of calls to the implicit right-hand-side function (PetscIFunctionIMEX() or PetscRHSFunctionImpl())
- Number of calls to the Jacobian (PetscIJacobianIMEX() or PetscIJacobian())
- Number of calls to the matrix-free Jacobian function (PetscJacobianFunctionIMEX_Linear(), PetscJacobianFunctionIMEX_JFNK(), PetscJacobianFunction_JFNK(), or PetscJacobianFunction_Linear()).
Expected screen output:
HyPar - Parallel (MPI) version with 1 processes
Compiled with PETSc time integration.
Reading solver inputs from file "solver.inp".
No. of dimensions : 2
No. of variables : 4
Domain size : 101 101
Processes along each dimension : 1 1
No. of ghosts pts : 3
No. of iter. : 1000
Restart iteration : 0
Time integration scheme : PETSc
Spatial discretization scheme (hyperbolic) : weno5
Split hyperbolic flux term? : yes
Interpolation type for hyperbolic term : components
Spatial discretization type (parabolic ) : nonconservative-2stage
Spatial discretization scheme (parabolic ) : 4
Time Step : 2.000000E-01
Check for conservation : no
Screen output iterations : 1
File output iterations : 99999
Initial solution file type : binary
Initial solution read mode : serial
Solution file write mode : serial
Solution file format : binary
Overwrite solution file : yes
Physical model : navierstokes2d
Partitioning domain.
Allocating data arrays.
Reading array from binary file initial.inp (Serial mode).
Volume integral of the initial solution:
0: 1.1370768428280035E+06
1: 0.0000000000000000E+00
2: 0.0000000000000000E+00
3: 2.4090461867112698E+11
Reading boundary conditions from "boundary.inp".
Boundary slip-wall: Along dimension 0 and face +1
Boundary slip-wall: Along dimension 0 and face -1
Boundary slip-wall: Along dimension 1 and face +1
Boundary slip-wall: Along dimension 1 and face -1
4 boundary condition(s) read.
Initializing solvers.
Reading WENO parameters from weno.inp.
Initializing physics. Model = "navierstokes2d"
Reading physical model inputs from file "physics.inp".
Setting up PETSc time integration...
Implicit-Explicit time-integration:-
Hyperbolic (f-df) term: Explicit
Hyperbolic (df) term: Implicit
Parabolic term: Implicit
Source term: Implicit
SolvePETSc(): Problem type is linear.
** Starting PETSc time integration **
0 TS dt 0.2 time 0.
Writing solution file op.bin.
TSAdapt 'basic': step 0 accepted t=0 + 2.000e-01 wlte=0.000404 family='arkimex' scheme=0:'4' dt=1.270e+00
Iteration: 1 Time: 2.000E-01 Max CFL: 4.409E+01 Max Diff. No.: -1.000E+00
1 TS dt 1.26968 time 0.2
TSAdapt 'basic': step 1 accepted t=0.2 + 1.270e+00 wlte=0.0909 family='arkimex' scheme=0:'4' dt=2.081e+00
Iteration: 2 Time: 1.470E+00 Max CFL: 7.227E+01 Max Diff. No.: -1.000E+00
2 TS dt 2.08133 time 1.46968
TSAdapt 'basic': step 2 accepted t=1.46968 + 2.081e+00 wlte= 0.14 family='arkimex' scheme=0:'4' dt=3.062e+00
Iteration: 3 Time: 3.551E+00 Max CFL: 1.063E+02 Max Diff. No.: -1.000E+00
3 TS dt 3.06203 time 3.55101
TSAdapt 'basic': step 3 accepted t=3.55101 + 3.062e+00 wlte=0.223 family='arkimex' scheme=0:'4' dt=4.010e+00
Iteration: 4 Time: 6.613E+00 Max CFL: 1.392E+02 Max Diff. No.: -1.000E+00
4 TS dt 4.00957 time 6.61303
TSAdapt 'basic': step 4 accepted t=6.61303 + 4.010e+00 wlte=0.186 family='arkimex' scheme=0:'4' dt=5.498e+00
Iteration: 5 Time: 1.062E+01 Max CFL: 1.909E+02 Max Diff. No.: -1.000E+00
5 TS dt 5.49814 time 10.6226
TSAdapt 'basic': step 5 accepted t=10.6226 + 5.498e+00 wlte=0.367 family='arkimex' scheme=0:'4' dt=6.358e+00
Iteration: 6 Time: 1.612E+01 Max CFL: 2.208E+02 Max Diff. No.: -1.000E+00
6 TS dt 6.35839 time 16.1207
TSAdapt 'basic': step 6 accepted t=16.1207 + 6.358e+00 wlte=0.156 family='arkimex' scheme=0:'4' dt=9.107e+00
Iteration: 7 Time: 2.248E+01 Max CFL: 3.163E+02 Max Diff. No.: -1.000E+00
7 TS dt 9.10749 time 22.4791
TSAdapt 'basic': step 7 accepted t=22.4791 + 9.107e+00 wlte=0.153 family='arkimex' scheme=0:'4' dt=1.310e+01
Iteration: 8 Time: 3.159E+01 Max CFL: 4.548E+02 Max Diff. No.: -1.000E+00
8 TS dt 13.0973 time 31.5866
TSAdapt 'basic': step 8 accepted t=31.5866 + 1.310e+01 wlte=0.129 family='arkimex' scheme=0:'4' dt=1.965e+01
Iteration: 9 Time: 4.468E+01 Max CFL: 6.825E+02 Max Diff. No.: -1.000E+00
9 TS dt 19.6528 time 44.6839
TSAdapt 'basic': step 9 accepted t=44.6839 + 1.965e+01 wlte=0.124 family='arkimex' scheme=0:'4' dt=2.983e+01
Iteration: 10 Time: 6.434E+01 Max CFL: 1.036E+03 Max Diff. No.: -1.000E+00
10 TS dt 29.8343 time 64.3367
TSAdapt 'basic': step 10 accepted t=64.3367 + 2.983e+01 wlte=0.362 family='arkimex' scheme=0:'4' dt=3.461e+01
Iteration: 11 Time: 9.417E+01 Max CFL: 1.202E+03 Max Diff. No.: -1.000E+00
11 TS dt 34.6126 time 94.171
TSAdapt 'basic': step 11 accepted t=94.171 + 3.461e+01 wlte=0.604 family='arkimex' scheme=0:'4' dt=3.533e+01
Iteration: 12 Time: 1.288E+02 Max CFL: 1.227E+03 Max Diff. No.: -1.000E+00
12 TS dt 35.3308 time 128.784
TSAdapt 'basic': step 12 accepted t=128.784 + 3.533e+01 wlte=0.783 family='arkimex' scheme=0:'4' dt=3.380e+01
Iteration: 13 Time: 1.641E+02 Max CFL: 1.174E+03 Max Diff. No.: -1.000E+00
13 TS dt 33.8018 time 164.114
TSAdapt 'basic': step 13 accepted t=164.114 + 3.380e+01 wlte=0.875 family='arkimex' scheme=0:'4' dt=2.084e+00
Iteration: 14 Time: 1.979E+02 Max CFL: 7.239E+01 Max Diff. No.: -1.000E+00
14 TS dt 2.08381 time 197.916
TSAdapt 'basic': step 14 accepted t=197.916 + 2.084e+00 wlte=0.0177 family='arkimex' scheme=0:'4' dt=5.144e+00
Iteration: 15 Time: 2.000E+02 Max CFL: 1.787E+02 Max Diff. No.: -1.000E+00
15 TS dt 5.14388 time 200.
** Completed PETSc time integration **
Writing solution file op.bin.
Computed errors:
L1 Error : 0.0000000000000000E+00
L2 Error : 0.0000000000000000E+00
Linfinity Error : 0.0000000000000000E+00
Conservation Errors:
0.0000000000000000E+00
0.0000000000000000E+00
0.0000000000000000E+00
0.0000000000000000E+00
Solver runtime (in seconds): 8.3499854999999997E+01
Total runtime (in seconds): 8.3511033999999995E+01
Deallocating arrays.
Finished.