3D Navier-Stokes Equations - Rising Thermal Bubble
Location: hypar/Examples/3D/NavierStokes3D/RisingThermalBubble_PETSc_IMEX (This directory contains all the input files needed to run this case.)
Governing equations: 3D Navier-Stokes Equations (navierstokes3d.h)
Domain: \(0 \le x,y,z < 1000\,{\rm m}\), "slip-wall" (_SLIP_WALL_) boundaries everywhere, with zero wall velocity.
Reference:
- Kelly, J. F., Giraldo, F. X., "Continuous and discontinuous Galerkin methods for a scalable three-dimensional nonhydrostatic atmospheric model: Limited-area mode", J. Comput. Phys., 231, 2012, pp. 7988-8008 (see section 5.1.2).
- Giraldo, F. X., Kelly, J. F., Constantinescu, E. M., "Implicit-Explicit Formulations of a Three-Dimensional Nonhydrostatic Unified Model of the Atmosphere (NUMA)", SIAM J. Sci. Comput., 35 (5), 2013, pp. B1162-B1194 (see section 4.1).
The problem is solved here using implicit-explicit (IMEX) time integration, where the hyperbolic flux is partitioned into its entropy and acoustic components with the former integrated explicitly and the latter integrated implicitly. See the following reference:
- Ghosh, D., Constantinescu, E. M., "Semi-Implicit Time Integration of Atmospheric Flows with Characteristic-Based Flux Partitioning", SIAM Journal on Scientific Computing, 38 (3), 2016, A1848-A1875, http://dx.doi.org/10.1137/15M1044369.
Initial solution: A warm bubble in cool ambient atmosphere. Note that in this example, the gravitational forces and rising of the bubble is along the y-axis.
Other parameters (all dimensional quantities are in SI units):
- Specific heat ratio \(\gamma = 1.4\) (NavierStokes3D::gamma)
- Universal gas constant \(R = 287.058\) (NavierStokes3D::R)
- Gravitational force per unit mass \(g = 9.8\) along y-axis (NavierStokes3D::grav_y)
- Reference density (at zero altitude) \(\rho_{ref} = 1.1612055171196529\) (NavierStokes3D::rho0)
- Reference pressure (at zero altitude) \(P_{ref} = 100000\) (NavierStokes3D::p0)
- Hydrostatic balance type 2 (NavierStokes3D::HB)
Numerical Method:
- Spatial discretization (hyperbolic): 5th order WENO (Interp1PrimFifthOrderWENO())
- Time integration: PETSc (SolvePETSc())
- Method Class: Additive Runge-Kutta method (TSARKIMEX - https://petsc.org/release/docs/manualpages/TS/TSARKIMEX.html)
- Specific method: ARK 2e (TSARKIMEX2E - https://petsc.org/release/docs/manualpages/TS/TSARKIMEX2E.html)
Input files required:
.petscrc
# See PETSc documentation for more details (https://petsc.org/release/overview/).
# Note that if the following are specified in this file, the corresponding inputs in solver.inp are *ignored*.
# + "-ts_dt" (time step size): ignores "dt" in solver.inp
# + "-ts_max_steps" (maximum number of time iterations): ignores "n_iter" in solver.inp
# + "-ts_max_time" (final simulation time): ignores "n_iter" X "dt" in solver.inp
# Use PETSc time-integration
-use-petscts
# Time integration scheme type - ARK
-ts_type arkimex
-ts_arkimex_type 2e
# Specify the terms to treat explicitly and implicitly
# In this example, the hyperbolic flux is partitioned
# into its entropy and acoustic components: f = [f-df] + [df]
# [f-df] - entropy component
# [df] - acoustic component
-hyperbolic_f_explicit # treat [f-df] explicitly
-hyperbolic_df_implicit # treat [df] implicitly
-source_implicit # treat source term implicitly
# thus, time step size is limited by the [f-df] term, i.e.,
# the flow velocity.
# no time-step adaptivity
-ts_adapt_type none
# For linear problens, tell nonlinear solver (SNES) to only use the linear solver (KSP)
-snes_type ksponly
# Linear solver (KSP) type
-ksp_type gmres
# Set relative tolerance
-ksp_rtol 1e-6
# Set absolute tolerance
-ksp_atol 1e-6
# Print residual
-ksp_monitor
# use a preconditioner for solving the system
-with_pc
# preconditioner type - block Jacobi
-pc_type sor
-pc_sor_omega 1.0
-pc_sor_its 10
solver.inp
begin
ndims 3
nvars 5
size 64 64 64
iproc 4 4 4
ghost 3
n_iter 100
restart_iter 0
hyp_space_scheme weno5
hyp_flux_split yes
hyp_interp_type components
dt 4.0
conservation_check no
screen_op_iter 1
file_op_iter 10
input_mode serial
ip_file_type binary
output_mode serial
op_file_format binary
op_overwrite no
model navierstokes3d
end
boundary.inp
6
slip-wall 0 1 0 0 0 1000.0 0 1000.0
0.0 0.0 0.0
slip-wall 0 -1 0 0 0 1000.0 0 1000.0
0.0 0.0 0.0
slip-wall 1 1 0 1000.0 0 0 0 1000.0
0.0 0.0 0.0
slip-wall 1 -1 0 1000.0 0 0 0 1000.0
0.0 0.0 0.0
slip-wall 2 1 0 1000.0 0 1000.0 0 0
0.0 0.0 0.0
slip-wall 2 -1 0 1000.0 0 1000.0 0 0
0.0 0.0 0.0
physics.inp
begin
gamma 1.4
upwinding rusanov
gravity 0.0 9.8 0.0
rho_ref 1.1612055171196529
p_ref 100000.0
R 287.058
HB 2
end
weno.inp (optional)
begin
mapped 0
borges 0
yc 0
no_limiting 1
epsilon 0.000001
p 2.0
rc 0.3
xi 0.001
end
To generate initial.inp (initial solution), compile and run the following code in the run directory.
/*
This code generates the initial solution for the rising
thermal bubble case for the 3D Navier-Stokes equations.
Note: this code allocates the global domain, so be careful
when using it for a large number of grid points.
*/
#include <stdio.h>
#include <stdlib.h>
#include <math.h>
#include <string.h>
{
return(exp(a*log(x)));
}
int main()
{
double gamma = 1.4;
double R = 287.058;
double rho_ref = 1.1612055171196529;
double p_ref = 100000.0;
double grav_x = 0.0;
double grav_y = 9.8;
double grav_z = 0.0;
int HB = 0;
int NI,NJ,NK,ndims;
char ip_file_type[50]; strcpy(ip_file_type,"ascii");
FILE *in;
printf("Reading file \"solver.inp\"...\n");
in = fopen("solver.inp","r");
if (!in) {
printf("Error: Input file \"solver.inp\" not found.\n");
return(0);
} else {
char word[500];
fscanf(in,"%s",word);
if (!strcmp(word, "begin")) {
while (strcmp(word, "end")) {
fscanf(in,"%s",word);
if (!strcmp(word, "ndims")) fscanf(in,"%d",&ndims);
else if (!strcmp(word, "size")) {
fscanf(in,"%d",&NI);
fscanf(in,"%d",&NJ);
fscanf(in,"%d",&NK);
} else if (!strcmp(word, "ip_file_type")) fscanf(in,"%s",ip_file_type);
}
} else printf("Error: Illegal format in solver.inp. Crash and burn!\n");
}
fclose(in);
printf("Reading file \"physics.inp\"...\n");
in = fopen("physics.inp","r");
if (!in) {
printf("Error: Input file \"physics.inp\" not found.\n");
return(0);
} else {
char word[500];
fscanf(in,"%s",word);
if (!strcmp(word, "begin")) {
while (strcmp(word, "end")) {
fscanf(in,"%s",word);
if (!strcmp(word, "rho_ref")) fscanf(in,"%lf",&rho_ref);
else if (!strcmp(word, "p_ref" )) fscanf(in,"%lf",&p_ref );
else if (!strcmp(word, "gamma" )) fscanf(in,"%lf",&gamma );
else if (!strcmp(word, "R" )) fscanf(in,"%lf",&R );
else if (!strcmp(word, "HB" )) fscanf(in,"%d" ,&HB );
else if (!strcmp(word, "gravity")) {
fscanf(in,"%lf",&grav_x );
fscanf(in,"%lf",&grav_y );
fscanf(in,"%lf",&grav_z );
}
}
} else printf("Error: Illegal format in physics.inp. Crash and burn!\n");
}
fclose(in);
if (ndims != 3) {
printf("ndims is not 3 in solver.inp. this code is to generate 3D initial conditions\n");
return(0);
}
if (HB != 2) {
printf("Error: Specify \"HB\" as 2 in physics.inp.\n");
}
if ((grav_x != 0.0) || (grav_z != 0.0)) {
printf("Error: gravity must be zero along x and z for this example.\n");
return(0);
}
printf("Grid:\t\t\t%d X %d X %d\n",NI,NJ,NK);
printf("Reference density and pressure: %lf, %lf.\n",rho_ref,p_ref);
int i,j,k;
double dx = 1000.0 / ((double)(NI-1));
double dy = 1000.0 / ((double)(NJ-1));
double dz = 1000.0 / ((double)(NK-1));
double *x, *y, *z, *U;
x = (double*) calloc (NI , sizeof(double));
y = (double*) calloc (NJ , sizeof(double));
z = (double*) calloc (NK , sizeof(double));
U = (double*) calloc (5*NI*NJ*NK, sizeof(double));
/* Initial perturbation center */
double xc = 500;
double yc = 260;
double zc = 500;
double Cp = gamma * R / (gamma-1.0);
/* initial perturbation parameters */
double pi = 4.0*atan(1.0);
double rc = 250.0;
double T_ref = p_ref / (R * rho_ref);
for (i = 0; i < NI; i++){
for (j = 0; j < NJ; j++){
for (k = 0; k < NK; k++){
x[i] = i*dx;
y[j] = j*dy;
z[k] = k*dz;
int p = i + NI*j + NI*NJ*k;
/* temperature peturbation */
double r = sqrt((x[i]-xc)*(x[i]-xc)+(y[j]-yc)*(y[j]-yc)+(z[k]-zc)*(z[k]-zc));
double dtheta = (r>rc ? 0.0 : (0.5*(1.0+cos(pi*r/rc))) );
double theta = T_ref + dtheta;
double Pexner = 1.0 - (grav_y*y[j])/(Cp*T_ref);
double rho = (p_ref/(R*theta)) * raiseto(Pexner, (1.0/(gamma-1.0)));
double E = rho * (R/(gamma-1.0)) * theta*Pexner;
U[5*p+0] = rho;
U[5*p+1] = 0.0;
U[5*p+2] = 0.0;
U[5*p+3] = 0.0;
U[5*p+4] = E;
}
}
}
FILE *out;
if (!strcmp(ip_file_type,"ascii")) {
printf("Error: sorry, ASCII format initial solution file not implemented. ");
printf("Please choose \"ip_file_format\" in solver.inp as \"binary\".\n");
return(0);
} else if ((!strcmp(ip_file_type,"binary")) || (!strcmp(ip_file_type,"bin"))) {
printf("Writing binary initial solution file initial.inp\n");
out = fopen("initial.inp","wb");
fwrite(x,sizeof(double),NI,out);
fwrite(y,sizeof(double),NJ,out);
fwrite(z,sizeof(double),NK,out);
fwrite(U,sizeof(double),5*NI*NJ*NK,out);
fclose(out);
}
free(x);
free(y);
free(z);
free(U);
return(0);
}
Output:
Note that iproc is set to
4 4 4
in solver.inp (i.e., 4 processors along x, 4 processors along y, and 4 processor along z). Thus, this example should be run with 64 MPI ranks (or change iproc).
After running the code, there should be 11 output files op_00000.bin, op_00001.bin, ... op_00010.bin; the first one is the solution at \(t=0\) and the final one is the solution at \(t=200\,{\rm s}\). Since HyPar::op_overwrite is set to no in solver.inp, separate files are written for solutions at each output time. All the files are binary (HyPar::op_file_format is set to binary in solver.inp).
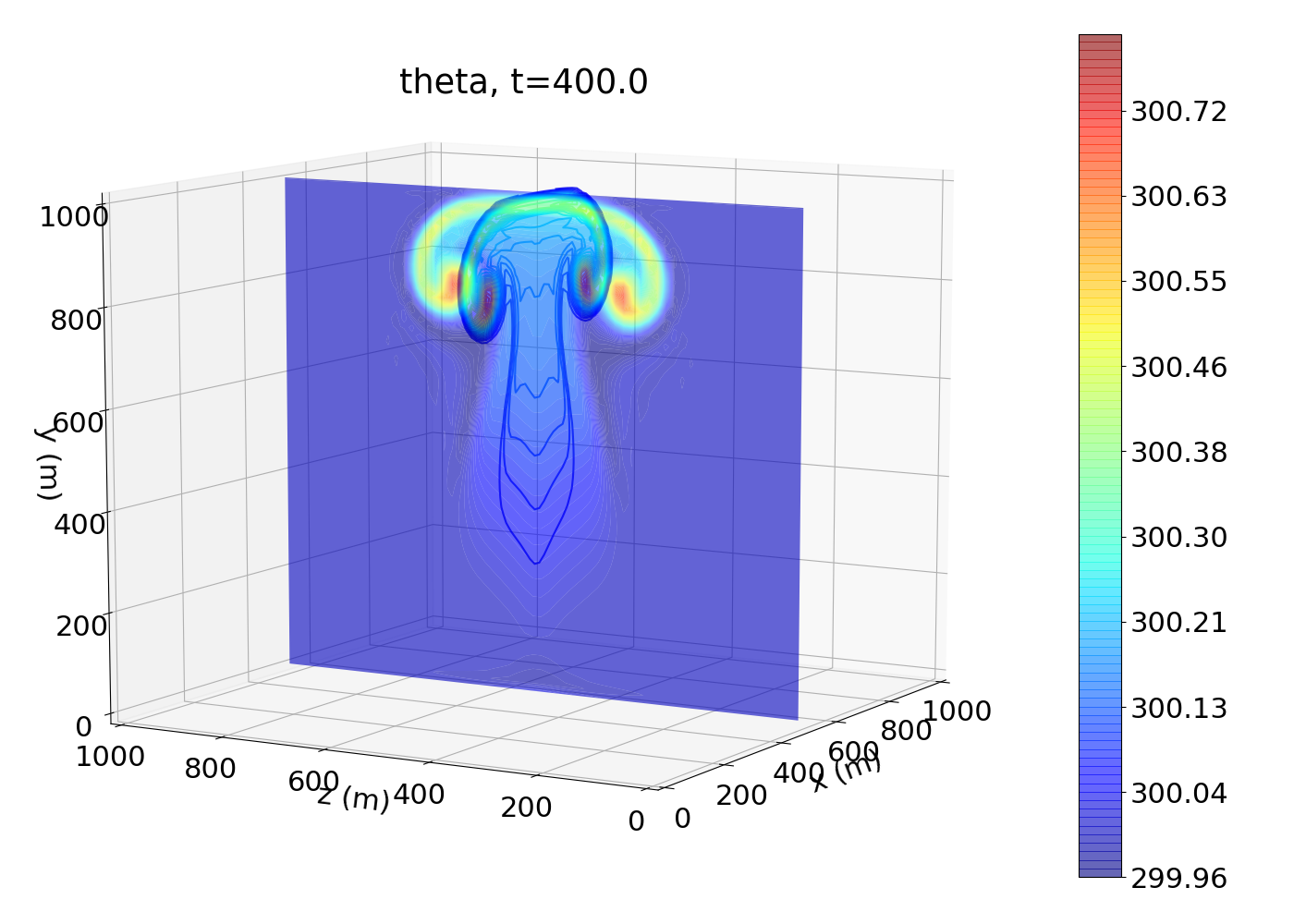
The binary solution file contains the conserved variables ( \(\rho,\rho u,\rho v,\rho w,e\)). The Python script plotSolution.py calculates the primitive and reference variables \(\rho,u,v,w,P,\theta,\rho_0,P_0,\pi,\theta_0\) (where the subscript \(0\) indicates the hydrostatic mean value) and plots 3D figures for \(\theta\) (potential temperature).
The following figure shows the potential temperature at the final time. Colored contours are plotted in the X-Y plane, and contour lines are plotted in the Z-Y plane:
The code Examples/3D/NavierStokes3D/RisingThermalBubble_PETSc_IMEX/aux/PostProcess.c can be used to convert the binary solution files to Tecplot or plain text files with the primitive and reference variables.
The file Extras/ExtractSlice.c can be used to extract a slice perpendicular to any dimension at a specified location along that dimension. The extract slice is written out in the same binary format as the original solutions files (with the same names op_xxxxx.bin) in a subdirectory called slices (Note: make the subdirectory called slices before running this code). The following code (Examples/3D/NavierStokes3D/RisingThermalBubble_PETSc_IMEX/aux/PostProcessSlice.c) can then be used (in the slices subdirectory) to convert the binary slice solution file (with conserved variables \(\rho,\rho u,\rho v,\rho w,e\)) to Tecplot or plain text files with the primitive and reference variables \(\rho,u,v,w,P,\theta,\rho_0,P_0,\pi,\theta_0\). Note that it needs the relevant solver.inp and physics.inp that can be created as follows:
- Copy the original solver.inp and physics.inp to the slices subdirectory.
- In solver.inp, set ndims as 2, and remove the component of size and iproc corresponding to the dimension being eliminated while extracting the slices (in this case, it is z or the 3rd component).
- In physics.inp, remove the component of gravity corresponding to the dimension perpendicular to the slice.
The file function_counts.dat reports the computational expense (in terms of the number of function counts):
100
9120
0
8820
300
300
200
8520
The numbers are, respectively,
- Time iterations
- Number of times the hyperbolic term was evaluated
- Number of times the parabolic term was evaluated
- Number of times the source term was evaluated
- Number of calls to the explicit right-hand-side function (PetscRHSFunctionIMEX() or PetscRHSFunctionExpl())
- Number of calls to the implicit right-hand-side function (PetscIFunctionIMEX() or PetscRHSFunctionImpl())
- Number of calls to the Jacobian (PetscIJacobianIMEX() or PetscIJacobian())
- Number of calls to the matrix-free Jacobian function (PetscJacobianFunctionIMEX_Linear(), PetscJacobianFunctionIMEX_JFNK(), PetscJacobianFunction_JFNK(), or PetscJacobianFunction_Linear()).
Expected screen output:
srun: job 10232779 queued and waiting for resources
srun: job 10232779 has been allocated resources
HyPar - Parallel (MPI) version with 64 processes
Compiled with PETSc time integration.
Allocated simulation object(s).
Reading solver inputs from file "solver.inp".
No. of dimensions : 3
No. of variables : 5
Domain size : 64 64 64
Processes along each dimension : 4 4 4
Exact solution domain size : 64 64 64
No. of ghosts pts : 3
No. of iter. : 100
Restart iteration : 0
Time integration scheme : PETSc
Spatial discretization scheme (hyperbolic) : weno5
Split hyperbolic flux term? : yes
Interpolation type for hyperbolic term : components
Spatial discretization type (parabolic ) : nonconservative-1stage
Spatial discretization scheme (parabolic ) : 2
Time Step : 4.000000E+00
Check for conservation : no
Screen output iterations : 1
File output iterations : 10
Initial solution file type : binary
Initial solution read mode : serial
Solution file write mode : serial
Solution file format : binary
Overwrite solution file : no
Physical model : navierstokes3d
Partitioning domain and allocating data arrays.
Reading array from binary file initial.inp (Serial mode).
Volume integral of the initial solution:
0: 1.1686650873135223E+09
1: 0.0000000000000000E+00
2: 0.0000000000000000E+00
3: 0.0000000000000000E+00
4: 2.4758406164981962E+14
Reading boundary conditions from boundary.inp.
Boundary slip-wall: Along dimension 0 and face +1
Boundary slip-wall: Along dimension 0 and face -1
Boundary slip-wall: Along dimension 1 and face +1
Boundary slip-wall: Along dimension 1 and face -1
Boundary slip-wall: Along dimension 2 and face +1
Boundary slip-wall: Along dimension 2 and face -1
6 boundary condition(s) read.
Initializing solvers.
Reading WENO parameters from weno.inp.
Initializing physics. Model = "navierstokes3d"
Reading physical model inputs from file "physics.inp".
Setting up PETSc time integration...
Setting up libROM interface.
PETSc: total number of computational points is 262144.
PETSc: total number of computational DOFs is 1310720.
Implicit-Explicit time-integration:-
Hyperbolic (f-df) term: Explicit
Hyperbolic (df) term: Implicit
Parabolic term: Implicit
Source term: Implicit
SolvePETSc(): Problem type is linear.
** Starting PETSc time integration **
Writing solution file op_00000.bin.
iter= 1 dt=4.000E+00 t=4.000E+00 CFL=8.750E+01 norm=8.3897E-01 wctime: 6.3E+00 (s)
iter= 2 dt=4.000E+00 t=8.000E+00 CFL=8.751E+01 norm=4.9377E-01 wctime: 5.1E+00 (s)
iter= 3 dt=4.000E+00 t=1.200E+01 CFL=8.751E+01 norm=3.0869E-01 wctime: 5.1E+00 (s)
iter= 4 dt=4.000E+00 t=1.600E+01 CFL=8.751E+01 norm=1.6931E-01 wctime: 5.2E+00 (s)
iter= 5 dt=4.000E+00 t=2.000E+01 CFL=8.751E+01 norm=6.9070E-02 wctime: 5.3E+00 (s)
iter= 6 dt=4.000E+00 t=2.400E+01 CFL=8.752E+01 norm=1.8199E-02 wctime: 5.6E+00 (s)
iter= 7 dt=4.000E+00 t=2.800E+01 CFL=8.752E+01 norm=5.2558E-02 wctime: 5.7E+00 (s)
iter= 8 dt=4.000E+00 t=3.200E+01 CFL=8.752E+01 norm=7.8811E-02 wctime: 5.6E+00 (s)
iter= 9 dt=4.000E+00 t=3.600E+01 CFL=8.753E+01 norm=7.9325E-02 wctime: 5.5E+00 (s)
iter= 10 dt=4.000E+00 t=4.000E+01 CFL=8.753E+01 norm=7.9721E-02 wctime: 5.6E+00 (s)
Writing solution file op_00001.bin.
iter= 11 dt=4.000E+00 t=4.400E+01 CFL=8.753E+01 norm=6.1882E-02 wctime: 5.7E+00 (s)
iter= 12 dt=4.000E+00 t=4.800E+01 CFL=8.755E+01 norm=5.4698E-02 wctime: 5.7E+00 (s)
iter= 13 dt=4.000E+00 t=5.200E+01 CFL=8.756E+01 norm=3.4127E-02 wctime: 5.7E+00 (s)
iter= 14 dt=4.000E+00 t=5.600E+01 CFL=8.757E+01 norm=3.0238E-02 wctime: 5.7E+00 (s)
iter= 15 dt=4.000E+00 t=6.000E+01 CFL=8.759E+01 norm=1.8179E-02 wctime: 5.7E+00 (s)
iter= 16 dt=4.000E+00 t=6.400E+01 CFL=8.760E+01 norm=1.9501E-02 wctime: 5.6E+00 (s)
iter= 17 dt=4.000E+00 t=6.800E+01 CFL=8.762E+01 norm=2.0295E-02 wctime: 5.6E+00 (s)
iter= 18 dt=4.000E+00 t=7.200E+01 CFL=8.763E+01 norm=1.9870E-02 wctime: 5.5E+00 (s)
iter= 19 dt=4.000E+00 t=7.600E+01 CFL=8.764E+01 norm=2.4144E-02 wctime: 5.5E+00 (s)
iter= 20 dt=4.000E+00 t=8.000E+01 CFL=8.765E+01 norm=2.1905E-02 wctime: 5.5E+00 (s)
Writing solution file op_00002.bin.
iter= 21 dt=4.000E+00 t=8.400E+01 CFL=8.767E+01 norm=2.5809E-02 wctime: 5.6E+00 (s)
iter= 22 dt=4.000E+00 t=8.800E+01 CFL=8.768E+01 norm=2.4004E-02 wctime: 5.5E+00 (s)
iter= 23 dt=4.000E+00 t=9.200E+01 CFL=8.769E+01 norm=2.6924E-02 wctime: 5.4E+00 (s)
iter= 24 dt=4.000E+00 t=9.600E+01 CFL=8.770E+01 norm=2.6488E-02 wctime: 5.4E+00 (s)
iter= 25 dt=4.000E+00 t=1.000E+02 CFL=8.771E+01 norm=2.8471E-02 wctime: 5.4E+00 (s)
iter= 26 dt=4.000E+00 t=1.040E+02 CFL=8.772E+01 norm=2.9182E-02 wctime: 5.4E+00 (s)
iter= 27 dt=4.000E+00 t=1.080E+02 CFL=8.773E+01 norm=3.0556E-02 wctime: 5.4E+00 (s)
iter= 28 dt=4.000E+00 t=1.120E+02 CFL=8.774E+01 norm=3.1884E-02 wctime: 5.4E+00 (s)
iter= 29 dt=4.000E+00 t=1.160E+02 CFL=8.774E+01 norm=3.3030E-02 wctime: 5.4E+00 (s)
iter= 30 dt=4.000E+00 t=1.200E+02 CFL=8.775E+01 norm=3.4593E-02 wctime: 5.4E+00 (s)
Writing solution file op_00003.bin.
iter= 31 dt=4.000E+00 t=1.240E+02 CFL=8.776E+01 norm=3.5780E-02 wctime: 5.4E+00 (s)
iter= 32 dt=4.000E+00 t=1.280E+02 CFL=8.776E+01 norm=3.7400E-02 wctime: 5.5E+00 (s)
iter= 33 dt=4.000E+00 t=1.320E+02 CFL=8.777E+01 norm=3.8749E-02 wctime: 5.4E+00 (s)
iter= 34 dt=4.000E+00 t=1.360E+02 CFL=8.777E+01 norm=4.0389E-02 wctime: 5.4E+00 (s)
iter= 35 dt=4.000E+00 t=1.400E+02 CFL=8.778E+01 norm=4.1922E-02 wctime: 5.5E+00 (s)
iter= 36 dt=4.000E+00 t=1.440E+02 CFL=8.778E+01 norm=4.3614E-02 wctime: 5.5E+00 (s)
iter= 37 dt=4.000E+00 t=1.480E+02 CFL=8.778E+01 norm=4.5323E-02 wctime: 5.5E+00 (s)
iter= 38 dt=4.000E+00 t=1.520E+02 CFL=8.779E+01 norm=4.7126E-02 wctime: 5.5E+00 (s)
iter= 39 dt=4.000E+00 t=1.560E+02 CFL=8.779E+01 norm=4.9019E-02 wctime: 5.5E+00 (s)
iter= 40 dt=4.000E+00 t=1.600E+02 CFL=8.779E+01 norm=5.1002E-02 wctime: 5.5E+00 (s)
Writing solution file op_00004.bin.
iter= 41 dt=4.000E+00 t=1.640E+02 CFL=8.779E+01 norm=5.3115E-02 wctime: 5.5E+00 (s)
iter= 42 dt=4.000E+00 t=1.680E+02 CFL=8.779E+01 norm=5.5348E-02 wctime: 5.4E+00 (s)
iter= 43 dt=4.000E+00 t=1.720E+02 CFL=8.779E+01 norm=5.7737E-02 wctime: 5.5E+00 (s)
iter= 44 dt=4.000E+00 t=1.760E+02 CFL=8.779E+01 norm=6.0271E-02 wctime: 5.4E+00 (s)
iter= 45 dt=4.000E+00 t=1.800E+02 CFL=8.779E+01 norm=6.2967E-02 wctime: 5.4E+00 (s)
iter= 46 dt=4.000E+00 t=1.840E+02 CFL=8.779E+01 norm=6.5806E-02 wctime: 5.4E+00 (s)
iter= 47 dt=4.000E+00 t=1.880E+02 CFL=8.779E+01 norm=6.8780E-02 wctime: 5.4E+00 (s)
iter= 48 dt=4.000E+00 t=1.920E+02 CFL=8.779E+01 norm=7.1853E-02 wctime: 5.4E+00 (s)
iter= 49 dt=4.000E+00 t=1.960E+02 CFL=8.778E+01 norm=7.5002E-02 wctime: 5.4E+00 (s)
iter= 50 dt=4.000E+00 t=2.000E+02 CFL=8.778E+01 norm=7.8176E-02 wctime: 5.4E+00 (s)
Writing solution file op_00005.bin.
iter= 51 dt=4.000E+00 t=2.040E+02 CFL=8.778E+01 norm=8.1351E-02 wctime: 5.4E+00 (s)
iter= 52 dt=4.000E+00 t=2.080E+02 CFL=8.778E+01 norm=8.4469E-02 wctime: 5.4E+00 (s)
iter= 53 dt=4.000E+00 t=2.120E+02 CFL=8.777E+01 norm=8.7517E-02 wctime: 5.4E+00 (s)
iter= 54 dt=4.000E+00 t=2.160E+02 CFL=8.777E+01 norm=9.0442E-02 wctime: 5.4E+00 (s)
iter= 55 dt=4.000E+00 t=2.200E+02 CFL=8.777E+01 norm=9.3247E-02 wctime: 5.4E+00 (s)
iter= 56 dt=4.000E+00 t=2.240E+02 CFL=8.776E+01 norm=9.5891E-02 wctime: 5.3E+00 (s)
iter= 57 dt=4.000E+00 t=2.280E+02 CFL=8.776E+01 norm=9.8388E-02 wctime: 5.3E+00 (s)
iter= 58 dt=4.000E+00 t=2.320E+02 CFL=8.776E+01 norm=1.0072E-01 wctime: 5.3E+00 (s)
iter= 59 dt=4.000E+00 t=2.360E+02 CFL=8.775E+01 norm=1.0289E-01 wctime: 5.4E+00 (s)
iter= 60 dt=4.000E+00 t=2.400E+02 CFL=8.775E+01 norm=1.0491E-01 wctime: 5.4E+00 (s)
Writing solution file op_00006.bin.
iter= 61 dt=4.000E+00 t=2.440E+02 CFL=8.775E+01 norm=1.0679E-01 wctime: 5.5E+00 (s)
iter= 62 dt=4.000E+00 t=2.480E+02 CFL=8.774E+01 norm=1.0855E-01 wctime: 5.4E+00 (s)
iter= 63 dt=4.000E+00 t=2.520E+02 CFL=8.774E+01 norm=1.1019E-01 wctime: 5.4E+00 (s)
iter= 64 dt=4.000E+00 t=2.560E+02 CFL=8.774E+01 norm=1.1175E-01 wctime: 5.4E+00 (s)
iter= 65 dt=4.000E+00 t=2.600E+02 CFL=8.773E+01 norm=1.1323E-01 wctime: 5.4E+00 (s)
iter= 66 dt=4.000E+00 t=2.640E+02 CFL=8.773E+01 norm=1.1466E-01 wctime: 5.4E+00 (s)
iter= 67 dt=4.000E+00 t=2.680E+02 CFL=8.773E+01 norm=1.1607E-01 wctime: 5.4E+00 (s)
iter= 68 dt=4.000E+00 t=2.720E+02 CFL=8.772E+01 norm=1.1745E-01 wctime: 5.4E+00 (s)
iter= 69 dt=4.000E+00 t=2.760E+02 CFL=8.772E+01 norm=1.1887E-01 wctime: 5.4E+00 (s)
iter= 70 dt=4.000E+00 t=2.800E+02 CFL=8.772E+01 norm=1.2031E-01 wctime: 5.4E+00 (s)
Writing solution file op_00007.bin.
iter= 71 dt=4.000E+00 t=2.840E+02 CFL=8.772E+01 norm=1.2183E-01 wctime: 5.4E+00 (s)
iter= 72 dt=4.000E+00 t=2.880E+02 CFL=8.771E+01 norm=1.2343E-01 wctime: 5.4E+00 (s)
iter= 73 dt=4.000E+00 t=2.920E+02 CFL=8.771E+01 norm=1.2515E-01 wctime: 5.4E+00 (s)
iter= 74 dt=4.000E+00 t=2.960E+02 CFL=8.771E+01 norm=1.2701E-01 wctime: 5.4E+00 (s)
iter= 75 dt=4.000E+00 t=3.000E+02 CFL=8.771E+01 norm=1.2903E-01 wctime: 5.4E+00 (s)
iter= 76 dt=4.000E+00 t=3.040E+02 CFL=8.770E+01 norm=1.3120E-01 wctime: 5.4E+00 (s)
iter= 77 dt=4.000E+00 t=3.080E+02 CFL=8.770E+01 norm=1.3355E-01 wctime: 5.4E+00 (s)
iter= 78 dt=4.000E+00 t=3.120E+02 CFL=8.770E+01 norm=1.3604E-01 wctime: 5.4E+00 (s)
iter= 79 dt=4.000E+00 t=3.160E+02 CFL=8.770E+01 norm=1.3869E-01 wctime: 5.4E+00 (s)
iter= 80 dt=4.000E+00 t=3.200E+02 CFL=8.769E+01 norm=1.4147E-01 wctime: 5.4E+00 (s)
Writing solution file op_00008.bin.
iter= 81 dt=4.000E+00 t=3.240E+02 CFL=8.769E+01 norm=1.4436E-01 wctime: 5.5E+00 (s)
iter= 82 dt=4.000E+00 t=3.280E+02 CFL=8.769E+01 norm=1.4733E-01 wctime: 5.4E+00 (s)
iter= 83 dt=4.000E+00 t=3.320E+02 CFL=8.769E+01 norm=1.5035E-01 wctime: 5.4E+00 (s)
iter= 84 dt=4.000E+00 t=3.360E+02 CFL=8.768E+01 norm=1.5338E-01 wctime: 5.4E+00 (s)
iter= 85 dt=4.000E+00 t=3.400E+02 CFL=8.768E+01 norm=1.5636E-01 wctime: 5.4E+00 (s)
iter= 86 dt=4.000E+00 t=3.440E+02 CFL=8.768E+01 norm=1.5925E-01 wctime: 5.4E+00 (s)
iter= 87 dt=4.000E+00 t=3.480E+02 CFL=8.768E+01 norm=1.6198E-01 wctime: 5.4E+00 (s)
iter= 88 dt=4.000E+00 t=3.520E+02 CFL=8.767E+01 norm=1.6452E-01 wctime: 5.4E+00 (s)
iter= 89 dt=4.000E+00 t=3.560E+02 CFL=8.767E+01 norm=1.6679E-01 wctime: 5.4E+00 (s)
iter= 90 dt=4.000E+00 t=3.600E+02 CFL=8.767E+01 norm=1.6875E-01 wctime: 5.4E+00 (s)
Writing solution file op_00009.bin.
iter= 91 dt=4.000E+00 t=3.640E+02 CFL=8.766E+01 norm=1.7036E-01 wctime: 5.4E+00 (s)
iter= 92 dt=4.000E+00 t=3.680E+02 CFL=8.766E+01 norm=1.7160E-01 wctime: 5.4E+00 (s)
iter= 93 dt=4.000E+00 t=3.720E+02 CFL=8.765E+01 norm=1.7247E-01 wctime: 5.3E+00 (s)
iter= 94 dt=4.000E+00 t=3.760E+02 CFL=8.764E+01 norm=1.7296E-01 wctime: 5.2E+00 (s)
iter= 95 dt=4.000E+00 t=3.800E+02 CFL=8.764E+01 norm=1.7312E-01 wctime: 5.1E+00 (s)
iter= 96 dt=4.000E+00 t=3.840E+02 CFL=8.763E+01 norm=1.7304E-01 wctime: 5.0E+00 (s)
iter= 97 dt=4.000E+00 t=3.880E+02 CFL=8.762E+01 norm=1.7295E-01 wctime: 4.9E+00 (s)
iter= 98 dt=4.000E+00 t=3.920E+02 CFL=8.760E+01 norm=1.7336E-01 wctime: 4.8E+00 (s)
iter= 99 dt=4.000E+00 t=3.960E+02 CFL=8.759E+01 norm=1.7536E-01 wctime: 4.7E+00 (s)
iter= 100 dt=4.000E+00 t=4.000E+02 CFL=8.757E+01 norm=1.8111E-01 wctime: 4.5E+00 (s)
Writing solution file op_00010.bin.
** Completed PETSc time integration (Final time: 400.000000), total wctime: 539.706822 (seconds) **
Solver runtime (in seconds): 5.4347381399999995E+02
Total runtime (in seconds): 5.4361646699999994E+02
Deallocating arrays.
Finished.