2D Euler Equations (with gravitational force) - Inertia-Gravity Waves
Location: hypar/Examples/2D/NavierStokes2D/InertiaGravityWave_PETSc_IMEX (This directory contains all the input files needed to run this case. If there is a Run.m, run it in MATLAB to quickly set up, run, and visualize the example).
Governing equations: 2D Euler Equations (navierstokes2d.h - By default, NavierStokes2D::Re is set to -1 which makes the code skip the parabolic terms, i.e., the 2D Euler equations are solved.)
Reference:
- W. C. Skamarock and J. B. Klemp, "Efficiency and accuracy of the Klemp-Wilhelmson timesplitting technique", Monthly Weather Review, 122 (1994), pp. 2623–2630.
- Giraldo, F.X., Restelli, M., "A study of spectral element and discontinuous Galerkin methods for the Navier–Stokes equations in nonhydrostatic mesoscale atmospheric modeling: Equation sets and test cases", J. Comput. Phys., 227, 2008, 3849–3877, (Section 3.1).
The problem is solved here using implicit-explicit (IMEX) time integration, where the hyperbolic flux is partitioned into its entropy and acoustic components with the former integrated explicitly and the latter integrated implicitly. See the following reference:
- Ghosh, D., Constantinescu, E. M., "Semi-Implicit Time Integration of Atmospheric Flows with Characteristic-Based Flux Partitioning", SIAM Journal on Scientific Computing, 38 (3), 2016, A1848-A1875, http://dx.doi.org/10.1137/15M1044369.
Domain: \(0 \le x \le 300,000\,m, 0 \le y \le 10,000\,m\), "periodic" (_PERIODIC_) boundary conditions along \(x\), "slip-wall" (_SLIP_WALL_) boundary conditions along \(y\).
Initial solution: See references above.
Other parameters (all dimensional quantities are in SI units):
- Specific heat ratio \(\gamma = 1.4\) (NavierStokes2D::gamma)
- Universal gas constant \(R = 287.058\) (NavierStokes2D::R)
- Gravitational force per unit mass \(g = 9.8\) along y-axis (NavierStokes2D::grav_y)
- Reference density (at zero altitude) \(\rho_{ref} = 1.1612055171196529\) (NavierStokes2D::rho0)
- Reference pressure (at zero altitude) \(P_{ref} = 100000\) (NavierStokes2D::p0)
- Hydrostatic balance type 3 (NavierStokes2D::HB)
- Brunt-Vaisala frequency 0.01 (NavierStokes2D::N_bv)
Numerical method:
- Spatial discretization (hyperbolic): 5th order compact upwind (Interp1PrimFifthOrderCompactUpwind())
- Time integration: PETSc (SolvePETSc())
- Method Class: Additive Runge-Kutta method (TSARKIMEX - https://petsc.org/release/docs/manualpages/TS/TSARKIMEX.html)
- Specific method: Kennedy-Carpenter ARK4 (TSARKIMEX4 - https://petsc.org/release/docs/manualpages/TS/TSARKIMEX4.html)
Input files required:
.petscrc
# See PETSc documentation for more details (https://petsc.org/release/overview/).
# Note that if the following are specified in this file, the corresponding inputs in solver.inp are *ignored*.
# + "-ts_dt" (time step size): ignores "dt" in solver.inp
# + "-ts_max_steps" (maximum number of time iterations): ignores "n_iter" in solver.inp
# + "-ts_max_time" (final simulation time): ignores "n_iter" X "dt" in solver.inp
# Use PETSc time-integration
-use-petscts
# Time integration scheme type - ARK
-ts_type arkimex
-ts_arkimex_type 4
# Specify the terms to treat explicitly and implicitly
# In this example, the hyperbolic flux is partitioned
# into its entropy and acoustic components: f = [f-df] + [df]
# [f-df] - entropy component
# [df] - acoustic component
-hyperbolic_f_explicit # treat [f-df] explicitly
-hyperbolic_df_implicit # treat [df] implicitly
-source_implicit # treat source term implicitly
# thus, time step size is limited by the [f-df] term, i.e.,
# the flow velocity.
# no time-step adaptivity
-ts_adapt_type none
# For linear problens, tell nonlinear solver (SNES) to only use the linear solver (KSP)
-snes_type ksponly
# Linear solver (KSP) type
-ksp_type gmres
# Set relative tolerance
-ksp_rtol 1e-6
# Set absolute tolerance
-ksp_atol 1e-6
# use a preconditioner for solving the system
-with_pc
# preconditioner type - SOR
-pc_type sor
-pc_sor_omega 1.0
-pc_sor_its 2
# apply right preconditioner
-ksp_pc_side RIGHT
solver.inp
begin
ndims 2
nvars 4
size 1200 50
iproc 12 1
ghost 3
n_iter 300
restart_iter 0
time_scheme rk
time_scheme_type ssprk3
hyp_space_scheme cupw5
hyp_flux_split yes
hyp_interp_type components
par_space_type nonconservative-2stage
par_space_scheme 4
dt 10.0
conservation_check no
screen_op_iter 1
file_op_iter 20
input_mode serial
ip_file_type binary
output_mode serial
op_file_format binary
op_overwrite no
model navierstokes2d
end
boundary.inp
4
periodic 0 1 0 0 0.0 10000.0
periodic 0 -1 0 0 0.0 10000.0
slip-wall 1 1 0.0 300000.0 0.0 0.0
0.0 0.0
slip-wall 1 -1 0.0 300000.0 0.0 0.0
0.0 0.0
physics.inp
begin
gamma 1.4
upwinding rusanov
gravity 0.0 9.8
rho_ref 1.1612055171196529
p_ref 100000.0
HB 3 0.01
R 287.058
end
To generate initial.inp (initial solution), compile and run the following code in the run directory.
#include <stdio.h>
#include <stdlib.h>
#include <math.h>
#include <string.h>
{
return(exp(a*log(x)));
}
int main()
{
double gamma = 1.4;
double R = 287.058;
double rho_ref = 1.1612055171196529;
double p_ref = 100000.0;
double grav_x = 0.0;
double grav_y = 9.8;
int HB = 0;
double BV = 0.0;
int NI,NK,ndims;
char ip_file_type[50];
strcpy(ip_file_type,"ascii");
FILE *in;
printf("Reading file \"solver.inp\"...\n");
in = fopen("solver.inp","r");
if (!in) {
printf ("Error: Input file \"solver.inp\" not found.\n");
return(1);
} else {
char word[500];
fscanf(in,"%s",word);
if (!strcmp(word, "begin")){
while (strcmp(word, "end")){
fscanf(in,"%s",word);
if (!strcmp(word, "ndims")) fscanf(in,"%d",&ndims);
else if (!strcmp(word, "size")) {
fscanf(in,"%d",&NI);
fscanf(in,"%d",&NK);
} else if (!strcmp(word, "ip_file_type")) fscanf(in,"%s",ip_file_type);
}
} else printf("Error: Illegal format in solver.inp. Crash and burn!\n");
}
fclose(in);
printf("Reading file \"physics.inp\"...\n");
in = fopen("physics.inp","r");
if (!in) {
printf("Error: Input file \"physics.inp\" not found.\n");
return(0);
} else {
char word[500];
fscanf(in,"%s",word);
if (!strcmp(word, "begin")) {
while (strcmp(word, "end")) {
fscanf(in,"%s",word);
if (!strcmp(word, "rho_ref")) fscanf(in,"%lf",&rho_ref);
else if (!strcmp(word, "p_ref" )) fscanf(in,"%lf",&p_ref );
else if (!strcmp(word, "gamma" )) fscanf(in,"%lf",&gamma );
else if (!strcmp(word, "R" )) fscanf(in,"%lf",&R );
else if (!strcmp(word, "HB" )) {
fscanf(in,"%d" ,&HB );
if (HB == 3) fscanf(in, "%lf", &BV);
} else if (!strcmp(word, "gravity")) {
fscanf(in,"%lf",&grav_x );
fscanf(in,"%lf",&grav_y );
}
}
} else printf("Error: Illegal format in physics.inp. Crash and burn!\n");
}
fclose(in);
if (ndims != 2) {
printf("ndims is not 2 in solver.inp. this code is to generate 2D initial conditions\n");
return(0);
}
if (HB != 3) {
printf("Error: Specify \"HB\" as 3 in physics.inp.\n");
}
if (grav_x != 0.0) {
printf("Error: Gravity force along x must be zero for HB = 3.\n");
return(0);
}
printf("Grid:\t\t\t%d X %d\n",NI,NK);
printf("Reference density and pressure: %lf, %lf.\n",rho_ref,p_ref);
/* Define the domain */
double xmin, xmax, zmin, zmax;
xmin = 0.0;
xmax = 300000;
zmin = 0.0;
zmax = 10000.0 ;
double Lx = xmax - xmin;
double Lz = zmax - zmin;
int i,k;
double dx = Lx / ((double)NI-1);
double dz = Lz / ((double)NK-1);
double *x, *z, *U;
FILE *out;
x = (double*) calloc (NI , sizeof(double));
z = (double*) calloc (NK , sizeof(double));
U = (double*) calloc (4*NI*NK, sizeof(double));
double inv_gamma_m1 = 1.0 / (gamma-1.0);
double Cp = gamma * R * inv_gamma_m1;
double Cv = R * inv_gamma_m1;
double T_ref = p_ref / (R*rho_ref);
/* initial perturbation parameters */
double pi = 4.0*atan(1.0);
double tc = 0.01;
double hc = 10000;
double ac = 5000;
double xc = 100000;
double uc = 20.0;
for (i = 0; i < NI; i++){
for (k = 0; k < NK; k++){
x[i] = xmin + i*dx;
z[k] = zmin + k*dz;
int p = i + NI*k;
/* temperature peturbation */
double dtheta = tc * sin(pi*z[k]/hc) / (1.0 + ((x[i]-xc)/ac)*((x[i]-xc)/ac));
double theta = T_ref*exp(BV*BV*z[k]/grav_y) + dtheta;
double Pexner = 1.0 + ((grav_y*grav_y)/(Cp*T_ref*BV*BV))*(exp(-BV*BV*z[k]/grav_y)-1.0);
double rho = (p_ref/(R*theta)) * raiseto(Pexner,inv_gamma_m1);
double E = Cv * theta * Pexner + 0.5 * (uc * uc);
U[4*p+0] = rho;
U[4*p+1] = rho*uc;
U[4*p+2] = 0.0;
U[4*p+3] = rho*E;
}
}
if (!strcmp(ip_file_type,"ascii")) {
printf("ASCII not supported. Use binary format\n");
} else if ((!strcmp(ip_file_type,"binary")) || (!strcmp(ip_file_type,"bin"))) {
printf("Writing binary initial solution file initial.inp\n");
out = fopen("initial.inp","wb");
fwrite(x,sizeof(double),NI,out);
fwrite(z,sizeof(double),NK,out);
fwrite(U,sizeof(double),4*NI*NK,out);
fclose(out);
}
free(x);
free(z);
free(U);
return(0);
}
Output:
Note that iproc is set to
12 1
in solver.inp (i.e., 12 processors along x, and 1 processor along y). Thus, this example should be run with 12 MPI ranks (or change iproc).
After running the code, there should be 16 output files op_00000.bin, op_00001.bin, ... op_00015.bin; the first one is the solution at \(t=0s\) and the final one is the solution at \(t=3000s\). Since HyPar::op_overwrite is set to no in solver.inp, separate files are written for solutions at each output time.
HyPar::op_file_format is set to binary in solver.inp, and thus, all the files are written out in the binary format, see WriteBinary(). The binary file contains the conserved variables \(\left(\rho, \rho u, \rho v, e\right)\). The following code converts these variables to the primitive variables of interest to atmospheric flows \(\left(\rho, u, v, p, \theta\right)\). It also writes out the hydrostatically balanced quantities \(\left(\rho_0,\pi_0, \theta_0\right)\) for this case that can be used to compute and plot the temperature and density perturbations. These variables are then written to either a tecplot2d or text file. (compile and run it in the run directory):
/*
Inertia-Gravity Waves:-
The code takes a binary solution file (that contains the
conserved variable (rho, rho*u, rho*v, e) as its input
and calculates the primitive atmospheric flow variables:
rho, u, v, P, theta, pi, rho0, P0, theta0, pi0
and writes them to a tecplot file.
*/
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#include <math.h>
typedef struct _parameters_{
double g, R, gamma, P_ref, rho_ref, Nbv;
int HB;
} Parameters;
void IncrementFilename(char *f)
{
if (f[7] == '9') {
f[7] = '0';
if (f[6] == '9') {
f[6] = '0';
if (f[5] == '9') {
f[5] = '0';
if (f[4] == '9') {
f[4] = '0';
if (f[3] == '9') {
f[3] = '0';
fprintf(stderr,"Warning: file increment hit max limit. Resetting to zero.\n");
} else {
f[3]++;
}
} else {
f[4]++;
}
} else {
f[5]++;
}
} else {
f[6]++;
}
} else {
f[7]++;
}
}
{
return(exp(a*log(x)));
}
{
printf("\tWriting tecplot solution file %s.\n",f);
FILE *out;
out = fopen(f,"w");
if (!out) {
fprintf(stderr,"Error: could not open %s for writing.\n",f);
return;
}
double *X = x;
double *Y = x+imax;
/* writing tecplot data file headers */
fprintf(out,"VARIABLES=\"I\",\"J\",\"X\",\"Y\",");
fprintf(out,"\"RHO\",\"U\",\"V\",\"P\",");
fprintf(out,"\"THETA\",\"RHO0\",\"P0\",");
fprintf(out,"\"PI0\",\"THETA0\",\n");
fprintf(out,"ZONE I=%d,J=%d,F=POINT\n",imax,jmax);
/* writing the data */
int i,j;
for (j=0; j<jmax; j++) {
for (i=0; i<imax; i++) {
int v, p = i + imax*j;
fprintf(out,"%4d %4d ",i,j);
fprintf(out,"%1.16E %1.16E ",X[i],Y[j]);
for (v=0; v<nvars; v++) fprintf(out,"%1.16E ",u[nvars*p+v]);
fprintf(out,"\n");
}
}
fclose(out);
return;
}
void WriteText2D(int nvars,int imax, int jmax,double *x,double *u,char *f)
{
printf("\tWriting text solution file %s.\n",f);
FILE *out;
out = fopen(f,"w");
if (!out) {
fprintf(stderr,"Error: could not open %s for writing.\n",f);
return;
}
double *X = x;
double *Y = x+imax;
/* writing the data */
int i,j;
for (j=0; j<jmax; j++) {
for (i=0; i<imax; i++) {
int v, p = i + imax*j;
fprintf(out,"%4d %4d ",i,j);
fprintf(out,"%1.16E %1.16E ",X[i],Y[j]);
for (v=0; v<nvars; v++) fprintf(out,"%1.16E ",u[nvars*p+v]);
fprintf(out,"\n");
}
}
fclose(out);
return;
}
int PostProcess(char *fname, char *oname, void *p, int flag)
{
Parameters *params = (Parameters*) p;
FILE *in; in = fopen(fname,"rb");
if (!in) return(-1);
printf("Reading file %s.\n",fname);
int ndims, nvars;
double *U,*x;
/* read the file headers */
fread(&ndims,sizeof(int),1,in);
fread(&nvars,sizeof(int),1,in);
/* some checks */
if (ndims != 2) {
printf("Error: ndims in %s not equal to 2!\n",fname);
return(1);
}
if (nvars != 4) {
printf("Error: nvars in %s not equal to 4!\n",fname);
return(1);
}
/* read dimensions */
int dims[ndims];
fread(dims,sizeof(int),ndims,in);
printf("Dimensions: %d x %d\n",dims[0],dims[1]);
printf("Nvars : %d\n",nvars);
/* allocate grid and solution arrays */
x = (double*) calloc (dims[0]+dims[1] ,sizeof(double));
U = (double*) calloc (dims[0]*dims[1]*nvars ,sizeof(double));
/* read grid and solution */
fread(x,sizeof(double),dims[0]+dims[1] ,in);
fread(U,sizeof(double),dims[0]*dims[1]*nvars,in);
/* done reading */
fclose(in);
int imax = dims[0];
int jmax = dims[1];
/* allocate primitive variable array (rho, u, v, P, theta, rho0, P0, pi0, theta0) */
int evars = 5;
double *Q = (double*) calloc ((nvars+evars)*imax*jmax,sizeof(double));
/* calculate primitive variables */
int i, j;
double *X = x;
double *Y = x+imax;
double g = params->g;
double R = params->R;
double gamma = params->gamma;
double P_ref = params->P_ref;
double rho_ref = params->rho_ref;
double T_ref = P_ref / (R*rho_ref);
double inv_gamma_m1 = 1.0 / (gamma-1.0);
double Cp = gamma * inv_gamma_m1 * R;
double BV = params->Nbv;
for (i=0; i<imax; i++) {
for (j=0; j<jmax; j++) {
int p = i + imax*j;
double rho0, theta0, Pexner, P0;
Pexner = 1.0 + ((g*g)/(Cp*T_ref*BV*BV))*(exp(-BV*BV*Y[j]/g)-1.0);
theta0 = T_ref * exp(BV*BV*Y[j]/g);
P0 = P_ref * raiseto(Pexner, gamma*inv_gamma_m1);
rho0 = rho_ref * raiseto(Pexner, inv_gamma_m1 ) * exp(-BV*BV*Y[j]/g);
double rho, uvel, vvel, E, P, theta;
rho = U[nvars*p+0];
uvel = U[nvars*p+1] / rho;
vvel = U[nvars*p+2] / rho;
E = U[nvars*p+3];
P = (gamma-1.0) * (E - 0.5*rho*(uvel*uvel+vvel*vvel));
theta = (E-0.5*rho*(uvel*uvel+vvel*vvel))/(Pexner*rho) * ((gamma-1.0)/R);
Q[(nvars+evars)*p+0] = rho;
Q[(nvars+evars)*p+1] = uvel;
Q[(nvars+evars)*p+2] = vvel;
Q[(nvars+evars)*p+3] = P;
Q[(nvars+evars)*p+4] = theta;
Q[(nvars+evars)*p+5] = rho0;
Q[(nvars+evars)*p+6] = P0;
Q[(nvars+evars)*p+7] = Pexner;
Q[(nvars+evars)*p+8] = theta0;
}
}
/* write Tecplot/Text file */
if (flag) WriteTecplot2D(nvars+evars,imax,jmax,x,Q,oname);
else WriteText2D (nvars+evars,imax,jmax,x,Q,oname);
/* clean up */
free(U);
free(Q);
free(x);
}
int main()
{
FILE *out1, *out2, *in, *inputs;
char filename[50], op_file_format[50], tecfile[50], overwrite[50];
int flag;
printf("Write tecplot file (1) or plain text file (0): ");
scanf("%d",&flag);
if ((flag != 1) && (flag != 0)) {
printf("Error: Invalid input. Should be 1 or 0.\n");
return(0);
}
printf("Reading solver.inp.\n");
inputs = fopen("solver.inp","r");
if (!inputs) {
fprintf(stderr,"Error: File \"solver.inp\" not found.\n");
return(1);
} else {
char word[100];
fscanf(inputs,"%s",word);
if (!strcmp(word, "begin")){
while (strcmp(word, "end")){
fscanf(inputs,"%s",word);
if (!strcmp(word, "op_file_format" )) fscanf(inputs,"%s" ,op_file_format);
else if (!strcmp(word, "op_overwrite" )) fscanf(inputs,"%s" ,overwrite );
}
}
fclose(inputs);
}
if (strcmp(op_file_format,"binary") && strcmp(op_file_format,"bin")) {
printf("Error: solution output needs to be in binary files.\n");
return(0);
}
Parameters params;
/* default values */
params.g = 9.8;
params.R = 287.058;
params.gamma = 1.4;
params.P_ref = 100000.0;
params.rho_ref = 100000.0 / (params.R * 300.0);
params.HB = 0;
params.Nbv = 0.0;
/* read these parameters from file */
printf("Reading physics.inp.\n");
inputs = fopen("physics.inp","r");
if (!inputs) {
fprintf(stderr,"Error: File \"physics.inp\" not found.\n");
return(1);
} else {
char word[100];
fscanf(inputs,"%s",word);
if (!strcmp(word, "begin")){
while (strcmp(word, "end")){
fscanf(inputs,"%s",word);
if (!strcmp(word, "gamma")) fscanf(inputs,"%lf",¶ms.gamma);
else if (!strcmp(word, "gravity")) {
double crap; fscanf(inputs,"%lf",&crap);
fscanf(inputs,"%lf",¶ms.g);
} else if (!strcmp(word,"p_ref")) fscanf(inputs,"%lf",¶ms.P_ref);
else if (!strcmp(word,"rho_ref")) fscanf(inputs,"%lf",¶ms.rho_ref);
else if (!strcmp(word,"HB")) {
fscanf(inputs,"%d",¶ms.HB);
if (params.HB == 3) fscanf(inputs,"%lf",¶ms.Nbv);
}
}
}
fclose(inputs);
}
if (params.HB != 3) {
printf("Error: \"HB\" must be specified as 3 in physics.inp.\n");
return(0);
}
if (!strcmp(overwrite,"no")) {
strcpy(filename,"op_00000.bin");
while(1) {
/* set filename */
strcpy(tecfile,filename);
tecfile[9] = 'd';
tecfile[10] = 'a';
tecfile[11] = 't';
int err = PostProcess(filename, tecfile, ¶ms, flag);
if (err == -1) {
printf("No more files found. Exiting.\n");
break;
}
IncrementFilename(filename);
}
} else if (!strcmp(overwrite,"yes")) {
strcpy(filename,"op.bin");
/* set filename */
strcpy(tecfile,filename);
tecfile[3] = 'd';
tecfile[4] = 'a';
tecfile[5] = 't';
int err = PostProcess(filename, tecfile, ¶ms, flag);
if (err == -1) {
printf("Error: op.bin not found.\n");
return(0);
}
}
return(0);
}
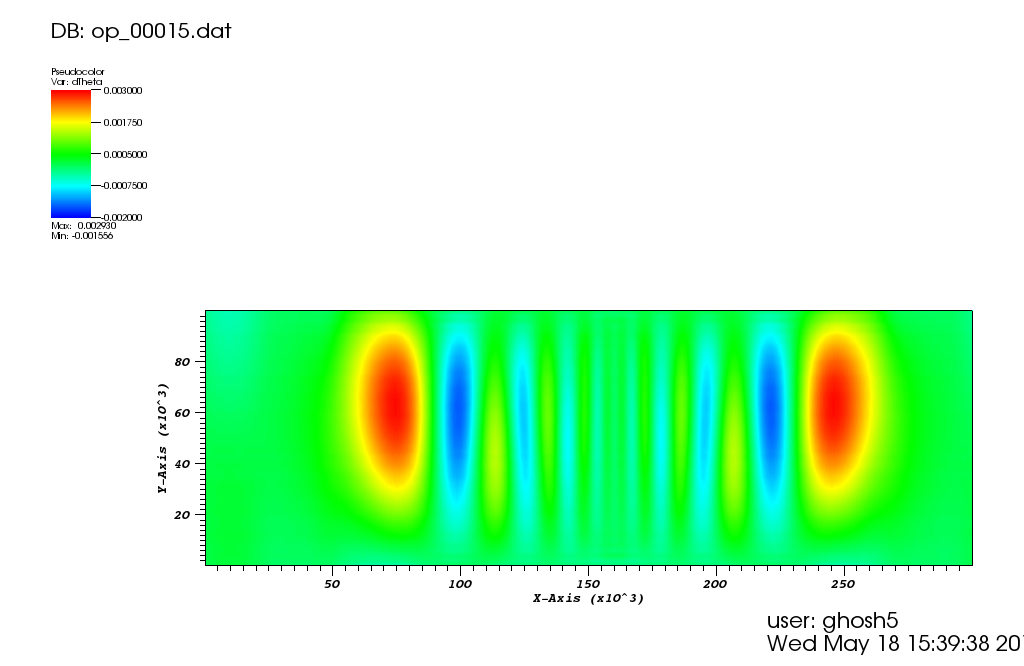
The following plot shows the potential temperature perturbation contours at the final time t=3000. It was plotted using VisIt (https://wci.llnl.gov/simulation/computer-codes/visit/) with tecplot2d format chosen in the above postprocessing code.
The file function_counts.dat reports the computational expense (in terms of the number of function counts):
300
39777
0
37977
1800
3300
1500
34677
The numbers are, respectively,
- Time iterations
- Number of times the hyperbolic term was evaluated
- Number of times the parabolic term was evaluated
- Number of times the source term was evaluated
- Number of calls to the explicit right-hand-side function (PetscRHSFunctionIMEX() or PetscRHSFunctionExpl())
- Number of calls to the implicit right-hand-side function (PetscIFunctionIMEX() or PetscRHSFunctionImpl())
- Number of calls to the Jacobian (PetscIJacobianIMEX() or PetscIJacobian())
- Number of calls to the matrix-free Jacobian function (PetscJacobianFunctionIMEX_Linear(), PetscJacobianFunctionIMEX_JFNK(), PetscJacobianFunction_JFNK(), or PetscJacobianFunction_Linear()).
Expected screen output:
HyPar - Parallel (MPI) version with 12 processes
Compiled with PETSc time integration.
Reading solver inputs from file "solver.inp".
No. of dimensions : 2
No. of variables : 4
Domain size : 1200 50
Processes along each dimension : 12 1
No. of ghosts pts : 3
No. of iter. : 300
Restart iteration : 0
Time integration scheme : PETSc
Spatial discretization scheme (hyperbolic) : cupw5
Split hyperbolic flux term? : yes
Interpolation type for hyperbolic term : components
Spatial discretization type (parabolic ) : nonconservative-2stage
Spatial discretization scheme (parabolic ) : 4
Time Step : 1.000000E+01
Check for conservation : no
Screen output iterations : 1
File output iterations : 20
Initial solution file type : binary
Initial solution read mode : serial
Solution file write mode : serial
Solution file format : binary
Overwrite solution file : no
Physical model : navierstokes2d
Partitioning domain.
Allocating data arrays.
Reading array from binary file initial.inp (Serial mode).
Volume integral of the initial solution:
0: 2.2722878895077519E+09
1: 4.5445757790155090E+10
2: 0.0000000000000000E+00
3: 4.4309563899845662E+14
Reading boundary conditions from "boundary.inp".
Boundary periodic: Along dimension 0 and face +1
Boundary periodic: Along dimension 0 and face -1
Boundary slip-wall: Along dimension 1 and face +1
Boundary slip-wall: Along dimension 1 and face -1
4 boundary condition(s) read.
Initializing solvers.
tridiagLUInit: File "lusolver.inp" not found. Using default values.
Initializing physics. Model = "navierstokes2d"
Reading physical model inputs from file "physics.inp".
Setting up PETSc time integration...
Implicit-Explicit time-integration:-
Hyperbolic (f-df) term: Explicit
Hyperbolic (df) term: Implicit
Parabolic term: Implicit
Source term: Implicit
SolvePETSc(): Problem type is linear.
** Starting PETSc time integration **
Writing solution file op_00000.bin.
Iteration: 1 Time: 1.000E+01 Max CFL: 1.701E+01 Max Diff. No.: -1.000E+00
Iteration: 2 Time: 2.000E+01 Max CFL: 1.701E+01 Max Diff. No.: -1.000E+00
Iteration: 3 Time: 3.000E+01 Max CFL: 1.701E+01 Max Diff. No.: -1.000E+00
Iteration: 4 Time: 4.000E+01 Max CFL: 1.701E+01 Max Diff. No.: -1.000E+00
Iteration: 5 Time: 5.000E+01 Max CFL: 1.701E+01 Max Diff. No.: -1.000E+00
Iteration: 6 Time: 6.000E+01 Max CFL: 1.701E+01 Max Diff. No.: -1.000E+00
Iteration: 7 Time: 7.000E+01 Max CFL: 1.701E+01 Max Diff. No.: -1.000E+00
Iteration: 8 Time: 8.000E+01 Max CFL: 1.701E+01 Max Diff. No.: -1.000E+00
Iteration: 9 Time: 9.000E+01 Max CFL: 1.701E+01 Max Diff. No.: -1.000E+00
Iteration: 10 Time: 1.000E+02 Max CFL: 1.701E+01 Max Diff. No.: -1.000E+00
Iteration: 11 Time: 1.100E+02 Max CFL: 1.701E+01 Max Diff. No.: -1.000E+00
Iteration: 12 Time: 1.200E+02 Max CFL: 1.701E+01 Max Diff. No.: -1.000E+00
Iteration: 13 Time: 1.300E+02 Max CFL: 1.701E+01 Max Diff. No.: -1.000E+00
Iteration: 14 Time: 1.400E+02 Max CFL: 1.701E+01 Max Diff. No.: -1.000E+00
Iteration: 15 Time: 1.500E+02 Max CFL: 1.701E+01 Max Diff. No.: -1.000E+00
Iteration: 16 Time: 1.600E+02 Max CFL: 1.701E+01 Max Diff. No.: -1.000E+00
Iteration: 17 Time: 1.700E+02 Max CFL: 1.701E+01 Max Diff. No.: -1.000E+00
Iteration: 18 Time: 1.800E+02 Max CFL: 1.701E+01 Max Diff. No.: -1.000E+00
Iteration: 19 Time: 1.900E+02 Max CFL: 1.701E+01 Max Diff. No.: -1.000E+00
Iteration: 20 Time: 2.000E+02 Max CFL: 1.701E+01 Max Diff. No.: -1.000E+00
Writing solution file op_00001.bin.
Iteration: 21 Time: 2.100E+02 Max CFL: 1.701E+01 Max Diff. No.: -1.000E+00
Iteration: 22 Time: 2.200E+02 Max CFL: 1.701E+01 Max Diff. No.: -1.000E+00
Iteration: 23 Time: 2.300E+02 Max CFL: 1.701E+01 Max Diff. No.: -1.000E+00
Iteration: 24 Time: 2.400E+02 Max CFL: 1.701E+01 Max Diff. No.: -1.000E+00
Iteration: 25 Time: 2.500E+02 Max CFL: 1.701E+01 Max Diff. No.: -1.000E+00
Iteration: 26 Time: 2.600E+02 Max CFL: 1.701E+01 Max Diff. No.: -1.000E+00
Iteration: 27 Time: 2.700E+02 Max CFL: 1.701E+01 Max Diff. No.: -1.000E+00
Iteration: 28 Time: 2.800E+02 Max CFL: 1.701E+01 Max Diff. No.: -1.000E+00
Iteration: 29 Time: 2.900E+02 Max CFL: 1.701E+01 Max Diff. No.: -1.000E+00
Iteration: 30 Time: 3.000E+02 Max CFL: 1.701E+01 Max Diff. No.: -1.000E+00
Iteration: 31 Time: 3.100E+02 Max CFL: 1.701E+01 Max Diff. No.: -1.000E+00
Iteration: 32 Time: 3.200E+02 Max CFL: 1.701E+01 Max Diff. No.: -1.000E+00
Iteration: 33 Time: 3.300E+02 Max CFL: 1.701E+01 Max Diff. No.: -1.000E+00
Iteration: 34 Time: 3.400E+02 Max CFL: 1.701E+01 Max Diff. No.: -1.000E+00
Iteration: 35 Time: 3.500E+02 Max CFL: 1.701E+01 Max Diff. No.: -1.000E+00
Iteration: 36 Time: 3.600E+02 Max CFL: 1.701E+01 Max Diff. No.: -1.000E+00
Iteration: 37 Time: 3.700E+02 Max CFL: 1.701E+01 Max Diff. No.: -1.000E+00
Iteration: 38 Time: 3.800E+02 Max CFL: 1.701E+01 Max Diff. No.: -1.000E+00
Iteration: 39 Time: 3.900E+02 Max CFL: 1.701E+01 Max Diff. No.: -1.000E+00
Iteration: 40 Time: 4.000E+02 Max CFL: 1.701E+01 Max Diff. No.: -1.000E+00
Writing solution file op_00002.bin.
Iteration: 41 Time: 4.100E+02 Max CFL: 1.701E+01 Max Diff. No.: -1.000E+00
Iteration: 42 Time: 4.200E+02 Max CFL: 1.701E+01 Max Diff. No.: -1.000E+00
Iteration: 43 Time: 4.300E+02 Max CFL: 1.701E+01 Max Diff. No.: -1.000E+00
Iteration: 44 Time: 4.400E+02 Max CFL: 1.701E+01 Max Diff. No.: -1.000E+00
Iteration: 45 Time: 4.500E+02 Max CFL: 1.701E+01 Max Diff. No.: -1.000E+00
Iteration: 46 Time: 4.600E+02 Max CFL: 1.701E+01 Max Diff. No.: -1.000E+00
Iteration: 47 Time: 4.700E+02 Max CFL: 1.701E+01 Max Diff. No.: -1.000E+00
Iteration: 48 Time: 4.800E+02 Max CFL: 1.701E+01 Max Diff. No.: -1.000E+00
Iteration: 49 Time: 4.900E+02 Max CFL: 1.701E+01 Max Diff. No.: -1.000E+00
Iteration: 50 Time: 5.000E+02 Max CFL: 1.701E+01 Max Diff. No.: -1.000E+00
Iteration: 51 Time: 5.100E+02 Max CFL: 1.701E+01 Max Diff. No.: -1.000E+00
Iteration: 52 Time: 5.200E+02 Max CFL: 1.701E+01 Max Diff. No.: -1.000E+00
Iteration: 53 Time: 5.300E+02 Max CFL: 1.701E+01 Max Diff. No.: -1.000E+00
Iteration: 54 Time: 5.400E+02 Max CFL: 1.701E+01 Max Diff. No.: -1.000E+00
Iteration: 55 Time: 5.500E+02 Max CFL: 1.701E+01 Max Diff. No.: -1.000E+00
Iteration: 56 Time: 5.600E+02 Max CFL: 1.701E+01 Max Diff. No.: -1.000E+00
Iteration: 57 Time: 5.700E+02 Max CFL: 1.701E+01 Max Diff. No.: -1.000E+00
Iteration: 58 Time: 5.800E+02 Max CFL: 1.701E+01 Max Diff. No.: -1.000E+00
Iteration: 59 Time: 5.900E+02 Max CFL: 1.701E+01 Max Diff. No.: -1.000E+00
Iteration: 60 Time: 6.000E+02 Max CFL: 1.701E+01 Max Diff. No.: -1.000E+00
Writing solution file op_00003.bin.
Iteration: 61 Time: 6.100E+02 Max CFL: 1.701E+01 Max Diff. No.: -1.000E+00
Iteration: 62 Time: 6.200E+02 Max CFL: 1.701E+01 Max Diff. No.: -1.000E+00
Iteration: 63 Time: 6.300E+02 Max CFL: 1.701E+01 Max Diff. No.: -1.000E+00
Iteration: 64 Time: 6.400E+02 Max CFL: 1.701E+01 Max Diff. No.: -1.000E+00
Iteration: 65 Time: 6.500E+02 Max CFL: 1.701E+01 Max Diff. No.: -1.000E+00
Iteration: 66 Time: 6.600E+02 Max CFL: 1.701E+01 Max Diff. No.: -1.000E+00
Iteration: 67 Time: 6.700E+02 Max CFL: 1.701E+01 Max Diff. No.: -1.000E+00
Iteration: 68 Time: 6.800E+02 Max CFL: 1.701E+01 Max Diff. No.: -1.000E+00
Iteration: 69 Time: 6.900E+02 Max CFL: 1.701E+01 Max Diff. No.: -1.000E+00
Iteration: 70 Time: 7.000E+02 Max CFL: 1.701E+01 Max Diff. No.: -1.000E+00
Iteration: 71 Time: 7.100E+02 Max CFL: 1.701E+01 Max Diff. No.: -1.000E+00
Iteration: 72 Time: 7.200E+02 Max CFL: 1.701E+01 Max Diff. No.: -1.000E+00
Iteration: 73 Time: 7.300E+02 Max CFL: 1.701E+01 Max Diff. No.: -1.000E+00
Iteration: 74 Time: 7.400E+02 Max CFL: 1.701E+01 Max Diff. No.: -1.000E+00
Iteration: 75 Time: 7.500E+02 Max CFL: 1.701E+01 Max Diff. No.: -1.000E+00
Iteration: 76 Time: 7.600E+02 Max CFL: 1.701E+01 Max Diff. No.: -1.000E+00
Iteration: 77 Time: 7.700E+02 Max CFL: 1.701E+01 Max Diff. No.: -1.000E+00
Iteration: 78 Time: 7.800E+02 Max CFL: 1.701E+01 Max Diff. No.: -1.000E+00
Iteration: 79 Time: 7.900E+02 Max CFL: 1.701E+01 Max Diff. No.: -1.000E+00
Iteration: 80 Time: 8.000E+02 Max CFL: 1.701E+01 Max Diff. No.: -1.000E+00
Writing solution file op_00004.bin.
Iteration: 81 Time: 8.100E+02 Max CFL: 1.701E+01 Max Diff. No.: -1.000E+00
Iteration: 82 Time: 8.200E+02 Max CFL: 1.701E+01 Max Diff. No.: -1.000E+00
Iteration: 83 Time: 8.300E+02 Max CFL: 1.701E+01 Max Diff. No.: -1.000E+00
Iteration: 84 Time: 8.400E+02 Max CFL: 1.701E+01 Max Diff. No.: -1.000E+00
Iteration: 85 Time: 8.500E+02 Max CFL: 1.701E+01 Max Diff. No.: -1.000E+00
Iteration: 86 Time: 8.600E+02 Max CFL: 1.701E+01 Max Diff. No.: -1.000E+00
Iteration: 87 Time: 8.700E+02 Max CFL: 1.701E+01 Max Diff. No.: -1.000E+00
Iteration: 88 Time: 8.800E+02 Max CFL: 1.701E+01 Max Diff. No.: -1.000E+00
Iteration: 89 Time: 8.900E+02 Max CFL: 1.701E+01 Max Diff. No.: -1.000E+00
Iteration: 90 Time: 9.000E+02 Max CFL: 1.701E+01 Max Diff. No.: -1.000E+00
Iteration: 91 Time: 9.100E+02 Max CFL: 1.701E+01 Max Diff. No.: -1.000E+00
Iteration: 92 Time: 9.200E+02 Max CFL: 1.701E+01 Max Diff. No.: -1.000E+00
Iteration: 93 Time: 9.300E+02 Max CFL: 1.701E+01 Max Diff. No.: -1.000E+00
Iteration: 94 Time: 9.400E+02 Max CFL: 1.701E+01 Max Diff. No.: -1.000E+00
Iteration: 95 Time: 9.500E+02 Max CFL: 1.701E+01 Max Diff. No.: -1.000E+00
Iteration: 96 Time: 9.600E+02 Max CFL: 1.701E+01 Max Diff. No.: -1.000E+00
Iteration: 97 Time: 9.700E+02 Max CFL: 1.701E+01 Max Diff. No.: -1.000E+00
Iteration: 98 Time: 9.800E+02 Max CFL: 1.701E+01 Max Diff. No.: -1.000E+00
Iteration: 99 Time: 9.900E+02 Max CFL: 1.701E+01 Max Diff. No.: -1.000E+00
Iteration: 100 Time: 1.000E+03 Max CFL: 1.701E+01 Max Diff. No.: -1.000E+00
Writing solution file op_00005.bin.
Iteration: 101 Time: 1.010E+03 Max CFL: 1.701E+01 Max Diff. No.: -1.000E+00
Iteration: 102 Time: 1.020E+03 Max CFL: 1.701E+01 Max Diff. No.: -1.000E+00
Iteration: 103 Time: 1.030E+03 Max CFL: 1.701E+01 Max Diff. No.: -1.000E+00
Iteration: 104 Time: 1.040E+03 Max CFL: 1.701E+01 Max Diff. No.: -1.000E+00
Iteration: 105 Time: 1.050E+03 Max CFL: 1.701E+01 Max Diff. No.: -1.000E+00
Iteration: 106 Time: 1.060E+03 Max CFL: 1.701E+01 Max Diff. No.: -1.000E+00
Iteration: 107 Time: 1.070E+03 Max CFL: 1.701E+01 Max Diff. No.: -1.000E+00
Iteration: 108 Time: 1.080E+03 Max CFL: 1.701E+01 Max Diff. No.: -1.000E+00
Iteration: 109 Time: 1.090E+03 Max CFL: 1.701E+01 Max Diff. No.: -1.000E+00
Iteration: 110 Time: 1.100E+03 Max CFL: 1.701E+01 Max Diff. No.: -1.000E+00
Iteration: 111 Time: 1.110E+03 Max CFL: 1.701E+01 Max Diff. No.: -1.000E+00
Iteration: 112 Time: 1.120E+03 Max CFL: 1.701E+01 Max Diff. No.: -1.000E+00
Iteration: 113 Time: 1.130E+03 Max CFL: 1.701E+01 Max Diff. No.: -1.000E+00
Iteration: 114 Time: 1.140E+03 Max CFL: 1.701E+01 Max Diff. No.: -1.000E+00
Iteration: 115 Time: 1.150E+03 Max CFL: 1.701E+01 Max Diff. No.: -1.000E+00
Iteration: 116 Time: 1.160E+03 Max CFL: 1.701E+01 Max Diff. No.: -1.000E+00
Iteration: 117 Time: 1.170E+03 Max CFL: 1.701E+01 Max Diff. No.: -1.000E+00
Iteration: 118 Time: 1.180E+03 Max CFL: 1.701E+01 Max Diff. No.: -1.000E+00
Iteration: 119 Time: 1.190E+03 Max CFL: 1.701E+01 Max Diff. No.: -1.000E+00
Iteration: 120 Time: 1.200E+03 Max CFL: 1.701E+01 Max Diff. No.: -1.000E+00
Writing solution file op_00006.bin.
Iteration: 121 Time: 1.210E+03 Max CFL: 1.701E+01 Max Diff. No.: -1.000E+00
Iteration: 122 Time: 1.220E+03 Max CFL: 1.701E+01 Max Diff. No.: -1.000E+00
Iteration: 123 Time: 1.230E+03 Max CFL: 1.701E+01 Max Diff. No.: -1.000E+00
Iteration: 124 Time: 1.240E+03 Max CFL: 1.701E+01 Max Diff. No.: -1.000E+00
Iteration: 125 Time: 1.250E+03 Max CFL: 1.701E+01 Max Diff. No.: -1.000E+00
Iteration: 126 Time: 1.260E+03 Max CFL: 1.701E+01 Max Diff. No.: -1.000E+00
Iteration: 127 Time: 1.270E+03 Max CFL: 1.701E+01 Max Diff. No.: -1.000E+00
Iteration: 128 Time: 1.280E+03 Max CFL: 1.701E+01 Max Diff. No.: -1.000E+00
Iteration: 129 Time: 1.290E+03 Max CFL: 1.701E+01 Max Diff. No.: -1.000E+00
Iteration: 130 Time: 1.300E+03 Max CFL: 1.701E+01 Max Diff. No.: -1.000E+00
Iteration: 131 Time: 1.310E+03 Max CFL: 1.701E+01 Max Diff. No.: -1.000E+00
Iteration: 132 Time: 1.320E+03 Max CFL: 1.701E+01 Max Diff. No.: -1.000E+00
Iteration: 133 Time: 1.330E+03 Max CFL: 1.701E+01 Max Diff. No.: -1.000E+00
Iteration: 134 Time: 1.340E+03 Max CFL: 1.701E+01 Max Diff. No.: -1.000E+00
Iteration: 135 Time: 1.350E+03 Max CFL: 1.701E+01 Max Diff. No.: -1.000E+00
Iteration: 136 Time: 1.360E+03 Max CFL: 1.701E+01 Max Diff. No.: -1.000E+00
Iteration: 137 Time: 1.370E+03 Max CFL: 1.701E+01 Max Diff. No.: -1.000E+00
Iteration: 138 Time: 1.380E+03 Max CFL: 1.701E+01 Max Diff. No.: -1.000E+00
Iteration: 139 Time: 1.390E+03 Max CFL: 1.701E+01 Max Diff. No.: -1.000E+00
Iteration: 140 Time: 1.400E+03 Max CFL: 1.701E+01 Max Diff. No.: -1.000E+00
Writing solution file op_00007.bin.
Iteration: 141 Time: 1.410E+03 Max CFL: 1.701E+01 Max Diff. No.: -1.000E+00
Iteration: 142 Time: 1.420E+03 Max CFL: 1.701E+01 Max Diff. No.: -1.000E+00
Iteration: 143 Time: 1.430E+03 Max CFL: 1.701E+01 Max Diff. No.: -1.000E+00
Iteration: 144 Time: 1.440E+03 Max CFL: 1.701E+01 Max Diff. No.: -1.000E+00
Iteration: 145 Time: 1.450E+03 Max CFL: 1.701E+01 Max Diff. No.: -1.000E+00
Iteration: 146 Time: 1.460E+03 Max CFL: 1.701E+01 Max Diff. No.: -1.000E+00
Iteration: 147 Time: 1.470E+03 Max CFL: 1.701E+01 Max Diff. No.: -1.000E+00
Iteration: 148 Time: 1.480E+03 Max CFL: 1.701E+01 Max Diff. No.: -1.000E+00
Iteration: 149 Time: 1.490E+03 Max CFL: 1.701E+01 Max Diff. No.: -1.000E+00
Iteration: 150 Time: 1.500E+03 Max CFL: 1.701E+01 Max Diff. No.: -1.000E+00
Iteration: 151 Time: 1.510E+03 Max CFL: 1.701E+01 Max Diff. No.: -1.000E+00
Iteration: 152 Time: 1.520E+03 Max CFL: 1.701E+01 Max Diff. No.: -1.000E+00
Iteration: 153 Time: 1.530E+03 Max CFL: 1.701E+01 Max Diff. No.: -1.000E+00
Iteration: 154 Time: 1.540E+03 Max CFL: 1.701E+01 Max Diff. No.: -1.000E+00
Iteration: 155 Time: 1.550E+03 Max CFL: 1.701E+01 Max Diff. No.: -1.000E+00
Iteration: 156 Time: 1.560E+03 Max CFL: 1.701E+01 Max Diff. No.: -1.000E+00
Iteration: 157 Time: 1.570E+03 Max CFL: 1.701E+01 Max Diff. No.: -1.000E+00
Iteration: 158 Time: 1.580E+03 Max CFL: 1.701E+01 Max Diff. No.: -1.000E+00
Iteration: 159 Time: 1.590E+03 Max CFL: 1.701E+01 Max Diff. No.: -1.000E+00
Iteration: 160 Time: 1.600E+03 Max CFL: 1.701E+01 Max Diff. No.: -1.000E+00
Writing solution file op_00008.bin.
Iteration: 161 Time: 1.610E+03 Max CFL: 1.701E+01 Max Diff. No.: -1.000E+00
Iteration: 162 Time: 1.620E+03 Max CFL: 1.701E+01 Max Diff. No.: -1.000E+00
Iteration: 163 Time: 1.630E+03 Max CFL: 1.701E+01 Max Diff. No.: -1.000E+00
Iteration: 164 Time: 1.640E+03 Max CFL: 1.701E+01 Max Diff. No.: -1.000E+00
Iteration: 165 Time: 1.650E+03 Max CFL: 1.701E+01 Max Diff. No.: -1.000E+00
Iteration: 166 Time: 1.660E+03 Max CFL: 1.701E+01 Max Diff. No.: -1.000E+00
Iteration: 167 Time: 1.670E+03 Max CFL: 1.701E+01 Max Diff. No.: -1.000E+00
Iteration: 168 Time: 1.680E+03 Max CFL: 1.701E+01 Max Diff. No.: -1.000E+00
Iteration: 169 Time: 1.690E+03 Max CFL: 1.701E+01 Max Diff. No.: -1.000E+00
Iteration: 170 Time: 1.700E+03 Max CFL: 1.701E+01 Max Diff. No.: -1.000E+00
Iteration: 171 Time: 1.710E+03 Max CFL: 1.701E+01 Max Diff. No.: -1.000E+00
Iteration: 172 Time: 1.720E+03 Max CFL: 1.701E+01 Max Diff. No.: -1.000E+00
Iteration: 173 Time: 1.730E+03 Max CFL: 1.701E+01 Max Diff. No.: -1.000E+00
Iteration: 174 Time: 1.740E+03 Max CFL: 1.701E+01 Max Diff. No.: -1.000E+00
Iteration: 175 Time: 1.750E+03 Max CFL: 1.701E+01 Max Diff. No.: -1.000E+00
Iteration: 176 Time: 1.760E+03 Max CFL: 1.701E+01 Max Diff. No.: -1.000E+00
Iteration: 177 Time: 1.770E+03 Max CFL: 1.701E+01 Max Diff. No.: -1.000E+00
Iteration: 178 Time: 1.780E+03 Max CFL: 1.701E+01 Max Diff. No.: -1.000E+00
Iteration: 179 Time: 1.790E+03 Max CFL: 1.701E+01 Max Diff. No.: -1.000E+00
Iteration: 180 Time: 1.800E+03 Max CFL: 1.701E+01 Max Diff. No.: -1.000E+00
Writing solution file op_00009.bin.
Iteration: 181 Time: 1.810E+03 Max CFL: 1.701E+01 Max Diff. No.: -1.000E+00
Iteration: 182 Time: 1.820E+03 Max CFL: 1.701E+01 Max Diff. No.: -1.000E+00
Iteration: 183 Time: 1.830E+03 Max CFL: 1.701E+01 Max Diff. No.: -1.000E+00
Iteration: 184 Time: 1.840E+03 Max CFL: 1.701E+01 Max Diff. No.: -1.000E+00
Iteration: 185 Time: 1.850E+03 Max CFL: 1.701E+01 Max Diff. No.: -1.000E+00
Iteration: 186 Time: 1.860E+03 Max CFL: 1.701E+01 Max Diff. No.: -1.000E+00
Iteration: 187 Time: 1.870E+03 Max CFL: 1.701E+01 Max Diff. No.: -1.000E+00
Iteration: 188 Time: 1.880E+03 Max CFL: 1.701E+01 Max Diff. No.: -1.000E+00
Iteration: 189 Time: 1.890E+03 Max CFL: 1.701E+01 Max Diff. No.: -1.000E+00
Iteration: 190 Time: 1.900E+03 Max CFL: 1.701E+01 Max Diff. No.: -1.000E+00
Iteration: 191 Time: 1.910E+03 Max CFL: 1.701E+01 Max Diff. No.: -1.000E+00
Iteration: 192 Time: 1.920E+03 Max CFL: 1.701E+01 Max Diff. No.: -1.000E+00
Iteration: 193 Time: 1.930E+03 Max CFL: 1.701E+01 Max Diff. No.: -1.000E+00
Iteration: 194 Time: 1.940E+03 Max CFL: 1.701E+01 Max Diff. No.: -1.000E+00
Iteration: 195 Time: 1.950E+03 Max CFL: 1.701E+01 Max Diff. No.: -1.000E+00
Iteration: 196 Time: 1.960E+03 Max CFL: 1.701E+01 Max Diff. No.: -1.000E+00
Iteration: 197 Time: 1.970E+03 Max CFL: 1.701E+01 Max Diff. No.: -1.000E+00
Iteration: 198 Time: 1.980E+03 Max CFL: 1.701E+01 Max Diff. No.: -1.000E+00
Iteration: 199 Time: 1.990E+03 Max CFL: 1.701E+01 Max Diff. No.: -1.000E+00
Iteration: 200 Time: 2.000E+03 Max CFL: 1.701E+01 Max Diff. No.: -1.000E+00
Writing solution file op_00010.bin.
Iteration: 201 Time: 2.010E+03 Max CFL: 1.701E+01 Max Diff. No.: -1.000E+00
Iteration: 202 Time: 2.020E+03 Max CFL: 1.701E+01 Max Diff. No.: -1.000E+00
Iteration: 203 Time: 2.030E+03 Max CFL: 1.701E+01 Max Diff. No.: -1.000E+00
Iteration: 204 Time: 2.040E+03 Max CFL: 1.701E+01 Max Diff. No.: -1.000E+00
Iteration: 205 Time: 2.050E+03 Max CFL: 1.701E+01 Max Diff. No.: -1.000E+00
Iteration: 206 Time: 2.060E+03 Max CFL: 1.701E+01 Max Diff. No.: -1.000E+00
Iteration: 207 Time: 2.070E+03 Max CFL: 1.701E+01 Max Diff. No.: -1.000E+00
Iteration: 208 Time: 2.080E+03 Max CFL: 1.701E+01 Max Diff. No.: -1.000E+00
Iteration: 209 Time: 2.090E+03 Max CFL: 1.701E+01 Max Diff. No.: -1.000E+00
Iteration: 210 Time: 2.100E+03 Max CFL: 1.701E+01 Max Diff. No.: -1.000E+00
Iteration: 211 Time: 2.110E+03 Max CFL: 1.701E+01 Max Diff. No.: -1.000E+00
Iteration: 212 Time: 2.120E+03 Max CFL: 1.701E+01 Max Diff. No.: -1.000E+00
Iteration: 213 Time: 2.130E+03 Max CFL: 1.701E+01 Max Diff. No.: -1.000E+00
Iteration: 214 Time: 2.140E+03 Max CFL: 1.701E+01 Max Diff. No.: -1.000E+00
Iteration: 215 Time: 2.150E+03 Max CFL: 1.701E+01 Max Diff. No.: -1.000E+00
Iteration: 216 Time: 2.160E+03 Max CFL: 1.701E+01 Max Diff. No.: -1.000E+00
Iteration: 217 Time: 2.170E+03 Max CFL: 1.701E+01 Max Diff. No.: -1.000E+00
Iteration: 218 Time: 2.180E+03 Max CFL: 1.701E+01 Max Diff. No.: -1.000E+00
Iteration: 219 Time: 2.190E+03 Max CFL: 1.701E+01 Max Diff. No.: -1.000E+00
Iteration: 220 Time: 2.200E+03 Max CFL: 1.701E+01 Max Diff. No.: -1.000E+00
Writing solution file op_00011.bin.
Iteration: 221 Time: 2.210E+03 Max CFL: 1.701E+01 Max Diff. No.: -1.000E+00
Iteration: 222 Time: 2.220E+03 Max CFL: 1.701E+01 Max Diff. No.: -1.000E+00
Iteration: 223 Time: 2.230E+03 Max CFL: 1.701E+01 Max Diff. No.: -1.000E+00
Iteration: 224 Time: 2.240E+03 Max CFL: 1.701E+01 Max Diff. No.: -1.000E+00
Iteration: 225 Time: 2.250E+03 Max CFL: 1.701E+01 Max Diff. No.: -1.000E+00
Iteration: 226 Time: 2.260E+03 Max CFL: 1.701E+01 Max Diff. No.: -1.000E+00
Iteration: 227 Time: 2.270E+03 Max CFL: 1.701E+01 Max Diff. No.: -1.000E+00
Iteration: 228 Time: 2.280E+03 Max CFL: 1.701E+01 Max Diff. No.: -1.000E+00
Iteration: 229 Time: 2.290E+03 Max CFL: 1.701E+01 Max Diff. No.: -1.000E+00
Iteration: 230 Time: 2.300E+03 Max CFL: 1.701E+01 Max Diff. No.: -1.000E+00
Iteration: 231 Time: 2.310E+03 Max CFL: 1.701E+01 Max Diff. No.: -1.000E+00
Iteration: 232 Time: 2.320E+03 Max CFL: 1.701E+01 Max Diff. No.: -1.000E+00
Iteration: 233 Time: 2.330E+03 Max CFL: 1.701E+01 Max Diff. No.: -1.000E+00
Iteration: 234 Time: 2.340E+03 Max CFL: 1.701E+01 Max Diff. No.: -1.000E+00
Iteration: 235 Time: 2.350E+03 Max CFL: 1.701E+01 Max Diff. No.: -1.000E+00
Iteration: 236 Time: 2.360E+03 Max CFL: 1.701E+01 Max Diff. No.: -1.000E+00
Iteration: 237 Time: 2.370E+03 Max CFL: 1.701E+01 Max Diff. No.: -1.000E+00
Iteration: 238 Time: 2.380E+03 Max CFL: 1.701E+01 Max Diff. No.: -1.000E+00
Iteration: 239 Time: 2.390E+03 Max CFL: 1.701E+01 Max Diff. No.: -1.000E+00
Iteration: 240 Time: 2.400E+03 Max CFL: 1.701E+01 Max Diff. No.: -1.000E+00
Writing solution file op_00012.bin.
Iteration: 241 Time: 2.410E+03 Max CFL: 1.701E+01 Max Diff. No.: -1.000E+00
Iteration: 242 Time: 2.420E+03 Max CFL: 1.701E+01 Max Diff. No.: -1.000E+00
Iteration: 243 Time: 2.430E+03 Max CFL: 1.701E+01 Max Diff. No.: -1.000E+00
Iteration: 244 Time: 2.440E+03 Max CFL: 1.701E+01 Max Diff. No.: -1.000E+00
Iteration: 245 Time: 2.450E+03 Max CFL: 1.701E+01 Max Diff. No.: -1.000E+00
Iteration: 246 Time: 2.460E+03 Max CFL: 1.701E+01 Max Diff. No.: -1.000E+00
Iteration: 247 Time: 2.470E+03 Max CFL: 1.701E+01 Max Diff. No.: -1.000E+00
Iteration: 248 Time: 2.480E+03 Max CFL: 1.701E+01 Max Diff. No.: -1.000E+00
Iteration: 249 Time: 2.490E+03 Max CFL: 1.701E+01 Max Diff. No.: -1.000E+00
Iteration: 250 Time: 2.500E+03 Max CFL: 1.701E+01 Max Diff. No.: -1.000E+00
Iteration: 251 Time: 2.510E+03 Max CFL: 1.701E+01 Max Diff. No.: -1.000E+00
Iteration: 252 Time: 2.520E+03 Max CFL: 1.701E+01 Max Diff. No.: -1.000E+00
Iteration: 253 Time: 2.530E+03 Max CFL: 1.701E+01 Max Diff. No.: -1.000E+00
Iteration: 254 Time: 2.540E+03 Max CFL: 1.701E+01 Max Diff. No.: -1.000E+00
Iteration: 255 Time: 2.550E+03 Max CFL: 1.701E+01 Max Diff. No.: -1.000E+00
Iteration: 256 Time: 2.560E+03 Max CFL: 1.701E+01 Max Diff. No.: -1.000E+00
Iteration: 257 Time: 2.570E+03 Max CFL: 1.701E+01 Max Diff. No.: -1.000E+00
Iteration: 258 Time: 2.580E+03 Max CFL: 1.701E+01 Max Diff. No.: -1.000E+00
Iteration: 259 Time: 2.590E+03 Max CFL: 1.701E+01 Max Diff. No.: -1.000E+00
Iteration: 260 Time: 2.600E+03 Max CFL: 1.701E+01 Max Diff. No.: -1.000E+00
Writing solution file op_00013.bin.
Iteration: 261 Time: 2.610E+03 Max CFL: 1.701E+01 Max Diff. No.: -1.000E+00
Iteration: 262 Time: 2.620E+03 Max CFL: 1.701E+01 Max Diff. No.: -1.000E+00
Iteration: 263 Time: 2.630E+03 Max CFL: 1.701E+01 Max Diff. No.: -1.000E+00
Iteration: 264 Time: 2.640E+03 Max CFL: 1.701E+01 Max Diff. No.: -1.000E+00
Iteration: 265 Time: 2.650E+03 Max CFL: 1.701E+01 Max Diff. No.: -1.000E+00
Iteration: 266 Time: 2.660E+03 Max CFL: 1.701E+01 Max Diff. No.: -1.000E+00
Iteration: 267 Time: 2.670E+03 Max CFL: 1.701E+01 Max Diff. No.: -1.000E+00
Iteration: 268 Time: 2.680E+03 Max CFL: 1.701E+01 Max Diff. No.: -1.000E+00
Iteration: 269 Time: 2.690E+03 Max CFL: 1.701E+01 Max Diff. No.: -1.000E+00
Iteration: 270 Time: 2.700E+03 Max CFL: 1.701E+01 Max Diff. No.: -1.000E+00
Iteration: 271 Time: 2.710E+03 Max CFL: 1.701E+01 Max Diff. No.: -1.000E+00
Iteration: 272 Time: 2.720E+03 Max CFL: 1.701E+01 Max Diff. No.: -1.000E+00
Iteration: 273 Time: 2.730E+03 Max CFL: 1.701E+01 Max Diff. No.: -1.000E+00
Iteration: 274 Time: 2.740E+03 Max CFL: 1.701E+01 Max Diff. No.: -1.000E+00
Iteration: 275 Time: 2.750E+03 Max CFL: 1.701E+01 Max Diff. No.: -1.000E+00
Iteration: 276 Time: 2.760E+03 Max CFL: 1.701E+01 Max Diff. No.: -1.000E+00
Iteration: 277 Time: 2.770E+03 Max CFL: 1.701E+01 Max Diff. No.: -1.000E+00
Iteration: 278 Time: 2.780E+03 Max CFL: 1.701E+01 Max Diff. No.: -1.000E+00
Iteration: 279 Time: 2.790E+03 Max CFL: 1.701E+01 Max Diff. No.: -1.000E+00
Iteration: 280 Time: 2.800E+03 Max CFL: 1.701E+01 Max Diff. No.: -1.000E+00
Writing solution file op_00014.bin.
Iteration: 281 Time: 2.810E+03 Max CFL: 1.701E+01 Max Diff. No.: -1.000E+00
Iteration: 282 Time: 2.820E+03 Max CFL: 1.701E+01 Max Diff. No.: -1.000E+00
Iteration: 283 Time: 2.830E+03 Max CFL: 1.701E+01 Max Diff. No.: -1.000E+00
Iteration: 284 Time: 2.840E+03 Max CFL: 1.701E+01 Max Diff. No.: -1.000E+00
Iteration: 285 Time: 2.850E+03 Max CFL: 1.701E+01 Max Diff. No.: -1.000E+00
Iteration: 286 Time: 2.860E+03 Max CFL: 1.701E+01 Max Diff. No.: -1.000E+00
Iteration: 287 Time: 2.870E+03 Max CFL: 1.701E+01 Max Diff. No.: -1.000E+00
Iteration: 288 Time: 2.880E+03 Max CFL: 1.701E+01 Max Diff. No.: -1.000E+00
Iteration: 289 Time: 2.890E+03 Max CFL: 1.701E+01 Max Diff. No.: -1.000E+00
Iteration: 290 Time: 2.900E+03 Max CFL: 1.701E+01 Max Diff. No.: -1.000E+00
Iteration: 291 Time: 2.910E+03 Max CFL: 1.701E+01 Max Diff. No.: -1.000E+00
Iteration: 292 Time: 2.920E+03 Max CFL: 1.701E+01 Max Diff. No.: -1.000E+00
Iteration: 293 Time: 2.930E+03 Max CFL: 1.701E+01 Max Diff. No.: -1.000E+00
Iteration: 294 Time: 2.940E+03 Max CFL: 1.701E+01 Max Diff. No.: -1.000E+00
Iteration: 295 Time: 2.950E+03 Max CFL: 1.701E+01 Max Diff. No.: -1.000E+00
Iteration: 296 Time: 2.960E+03 Max CFL: 1.701E+01 Max Diff. No.: -1.000E+00
Iteration: 297 Time: 2.970E+03 Max CFL: 1.701E+01 Max Diff. No.: -1.000E+00
Iteration: 298 Time: 2.980E+03 Max CFL: 1.701E+01 Max Diff. No.: -1.000E+00
Iteration: 299 Time: 2.990E+03 Max CFL: 1.701E+01 Max Diff. No.: -1.000E+00
Iteration: 300 Time: 3.000E+03 Max CFL: 1.701E+01 Max Diff. No.: -1.000E+00
Writing solution file op_00015.bin.
** Completed PETSc time integration **
Computed errors:
L1 Error : 0.0000000000000000E+00
L2 Error : 0.0000000000000000E+00
Linfinity Error : 0.0000000000000000E+00
Conservation Errors:
0.0000000000000000E+00
0.0000000000000000E+00
0.0000000000000000E+00
0.0000000000000000E+00
Solver runtime (in seconds): 1.4787465340000001E+03
Total runtime (in seconds): 1.4787629099999999E+03
Deallocating arrays.
Finished.