2D Euler Equations - Density Sine Wave
Location: hypar/Examples/2D/NavierStokes2D/DensitySineWave_SparseGrids (This directory contains all the input files needed to run this case.)
Governing equations: 2D Euler Equations (navierstokes2d.h - By default, NavierStokes2D::Re is set to -1 which makes the code skip the parabolic terms, i.e., the 2D Euler equations are solved.)
Domain: \(0 \le x,y \le 1\), "periodic" (_PERIODIC_) boundary conditions.
Initial solution: The freestream flow is given by
\begin{equation} \rho_\infty = 1,\ u_\infty = 1,\ v_\infty = 1,\ p_\infty = \frac{1}{\gamma} \end{equation}
and the density wave is
\begin{align} \rho = \rho_\infty + \frac{1}{10} \sin\left(2\pi x\right)\cos\left(2\pi y\right) \end{align}
Numerical method:
- Spatial discretization (hyperbolic): 5th order compact upwind (Interp1PrimFifthOrderCompactUpwind())
- Time integration: RK4 (TimeRK(), _RK_44_)
Input files required:
sparse_grids.inp
begin
log2_imin 3
interp_order 6
write_sg_solutions no
write_sg_errors no
end
Note: The remaining files are the same as what would be required for a conventional (non-sparse-grids) simulation.
solver.inp
begin
ndims 2
nvars 4
size 128 128
ghost 3
n_iter 400
restart_iter 0
time_scheme rk
time_scheme_type 44
hyp_space_scheme cupw5
hyp_flux_split no
hyp_interp_type components
par_space_type nonconservative-2stage
par_space_scheme 4
dt 0.0025
conservation_check no
screen_op_iter 10
file_op_iter 40
op_file_format tecplot2d
ip_file_type binary
input_mode serial
output_mode serial
op_overwrite no
model navierstokes2d
end
boundary.inp
4
periodic 0 1 0 0 0 1
periodic 0 -1 0 0 0 1
periodic 1 1 0 1 0 0
periodic 1 -1 0 1 0 0
physics.inp
begin
gamma 1.3999999999999999e+00
upwinding roe
Pr 7.1999999999999997e-01
Re -1.0000000000000000e+00
Minf 1.0000000000000000e+00
gravity 0.0000000000000000e+00 0.0000000000000000e+00
rho_ref 1.0000000000000000e+00
p_ref 1.0000000000000000e+00
HB 0
R 1.0000000000000000e+00
end
lusolver.inp
begin
reducedsolvetype jacobi
evaluate_norm 1
maxiter 10
atol 9.9999999999999998e-13
rtol 1.0000000000000000e-10
verbose 0
end
To generate initial.inp (initial solution) and exact.inp (exact solution), compile and run the following code in the run directory. (It is the same file as the one used in running a conventional non-sparse-grids simulation).
#include <stdio.h>
#include <stdlib.h>
#include <math.h>
#include <string.h>
double power(double x,double a)
{
return(exp(a*log(x)));
}
int main(){
const double pi = 4.0*atan(1.0);
const double GAMMA = 1.4;
int NI,NJ,ndims,n_iter;
double tf, dt;
char ip_file_type[50]; strcpy(ip_file_type,"ascii");
FILE *in, *out;
printf("Reading file \"solver.inp\"...\n");
in = fopen("solver.inp","r");
if (!in) {
printf("Error: Input file \"solver.inp\" not found. Default values will be used.\n");
return(0);
} else {
char word[500];
fscanf(in,"%s",word);
if (!strcmp(word, "begin")) {
while (strcmp(word, "end")) {
fscanf(in,"%s",word);
if (!strcmp(word, "ndims")) fscanf(in,"%d",&ndims);
else if (!strcmp(word, "size")) {
fscanf(in,"%d",&NI);
fscanf(in,"%d",&NJ);
} else if (!strcmp(word, "n_iter")) fscanf(in,"%d",&n_iter);
else if (!strcmp(word, "dt")) fscanf(in,"%lf",&dt);
else if (!strcmp(word, "ip_file_type")) fscanf(in,"%s",ip_file_type);
}
} else printf("Error: Illegal format in solver.inp. Crash and burn!\n");
}
fclose(in);
if (ndims != 2) {
printf("ndims is not 2 in solver.inp. this code is to generate 2D exact solution\n");
return(0);
}
printf("Grid:\t\t\t%d X %d\n",NI,NJ);
int i,j;
double dx = 1.0 / ((double)NI);
double dy = 1.0 / ((double)NJ);
tf = (double)n_iter * dt;
printf("Final time: %lf\n", tf);
double *x, *y, *u0, *u1, *u2, *u3;
x = (double*) calloc (NI , sizeof(double));
y = (double*) calloc (NJ , sizeof(double));
u0 = (double*) calloc (NI*NJ, sizeof(double));
u1 = (double*) calloc (NI*NJ, sizeof(double));
u2 = (double*) calloc (NI*NJ, sizeof(double));
u3 = (double*) calloc (NI*NJ, sizeof(double));
double rho_inf = 1.0;
double drho = 0.1;
double u_inf = 1.0;
double v_inf = 1.0;
double P_inf = 1.0/GAMMA;
/* Initial solution */
for (i = 0; i < NI; i++) {
for (j = 0; j < NJ; j++) {
x[i] = i*dx;
y[j] = j*dy;
int p = NJ*i + j;
double rho, u, v, P;
rho = rho_inf + drho * sin(2*pi*x[i]) * cos(2*pi*y[j]);
P = P_inf;
u = u_inf;
v = v_inf;
u0[p] = rho;
u1[p] = rho*u;
u2[p] = rho*v;
u3[p] = P/(GAMMA-1.0) + 0.5*rho*(u*u+v*v);
}
}
if (!strcmp(ip_file_type,"ascii")) {
printf("Writing ASCII initial solution file initial.inp\n");
out = fopen("initial.inp","w");
for (i = 0; i < NI; i++) fprintf(out,"%lf ",x[i]);
fprintf(out,"\n");
for (j = 0; j < NJ; j++) fprintf(out,"%lf ",y[j]);
fprintf(out,"\n");
for (j = 0; j < NJ; j++) {
for (i = 0; i < NI; i++) {
int p = NJ*i + j;
fprintf(out,"%lf ",u0[p]);
}
}
fprintf(out,"\n");
for (j = 0; j < NJ; j++) {
for (i = 0; i < NI; i++) {
int p = NJ*i + j;
fprintf(out,"%lf ",u1[p]);
}
}
fprintf(out,"\n");
for (j = 0; j < NJ; j++) {
for (i = 0; i < NI; i++) {
int p = NJ*i + j;
fprintf(out,"%lf ",u2[p]);
}
}
fprintf(out,"\n");
for (j = 0; j < NJ; j++) {
for (i = 0; i < NI; i++) {
int p = NJ*i + j;
fprintf(out,"%lf ",u3[p]);
}
}
fprintf(out,"\n");
fclose(out);
} else if ((!strcmp(ip_file_type,"binary")) || (!strcmp(ip_file_type,"bin"))) {
printf("Writing binary initial solution file initial.inp\n");
out = fopen("initial.inp","wb");
fwrite(x,sizeof(double),NI,out);
fwrite(y,sizeof(double),NJ,out);
double *U = (double*) calloc (4*NI*NJ,sizeof(double));
for (i=0; i < NI; i++) {
for (j = 0; j < NJ; j++) {
int p = NJ*i + j;
int q = NI*j + i;
U[4*q+0] = u0[p];
U[4*q+1] = u1[p];
U[4*q+2] = u2[p];
U[4*q+3] = u3[p];
}
}
fwrite(U,sizeof(double),4*NI*NJ,out);
free(U);
fclose(out);
}
/* Exact solution */
for (i = 0; i < NI; i++) {
for (j = 0; j < NJ; j++) {
x[i] = i*dx;
y[j] = j*dy;
int p = NJ*i + j;
double rho, u, v, P;
rho = rho_inf + drho * sin(2*pi*(x[i]-u_inf*tf)) * cos(2*pi*(y[j]-v_inf*tf));
P = P_inf;
u = u_inf;
v = v_inf;
u0[p] = rho;
u1[p] = rho*u;
u2[p] = rho*v;
u3[p] = P/(GAMMA-1.0) + 0.5*rho*(u*u+v*v);
}
}
if (!strcmp(ip_file_type,"ascii")) {
printf("Writing ASCII exact solution file exact.inp\n");
out = fopen("exact.inp","w");
for (i = 0; i < NI; i++) fprintf(out,"%lf ",x[i]);
fprintf(out,"\n");
for (j = 0; j < NJ; j++) fprintf(out,"%lf ",y[j]);
fprintf(out,"\n");
for (j = 0; j < NJ; j++) {
for (i = 0; i < NI; i++) {
int p = NJ*i + j;
fprintf(out,"%lf ",u0[p]);
}
}
fprintf(out,"\n");
for (j = 0; j < NJ; j++) {
for (i = 0; i < NI; i++) {
int p = NJ*i + j;
fprintf(out,"%lf ",u1[p]);
}
}
fprintf(out,"\n");
for (j = 0; j < NJ; j++) {
for (i = 0; i < NI; i++) {
int p = NJ*i + j;
fprintf(out,"%lf ",u2[p]);
}
}
fprintf(out,"\n");
for (j = 0; j < NJ; j++) {
for (i = 0; i < NI; i++) {
int p = NJ*i + j;
fprintf(out,"%lf ",u3[p]);
}
}
fprintf(out,"\n");
fclose(out);
} else if ((!strcmp(ip_file_type,"binary")) || (!strcmp(ip_file_type,"bin"))) {
printf("Writing binary exact solution file exact.inp\n");
out = fopen("exact.inp","wb");
fwrite(x,sizeof(double),NI,out);
fwrite(y,sizeof(double),NJ,out);
double *U = (double*) calloc (4*NI*NJ,sizeof(double));
for (i=0; i < NI; i++) {
for (j = 0; j < NJ; j++) {
int p = NJ*i + j;
int q = NI*j + i;
U[4*q+0] = u0[p];
U[4*q+1] = u1[p];
U[4*q+2] = u2[p];
U[4*q+3] = u3[p];
}
}
fwrite(U,sizeof(double),4*NI*NJ,out);
free(U);
fclose(out);
}
free(x);
free(y);
free(u0);
free(u1);
free(u2);
free(u3);
return(0);
}
Output:
Note that iproc does not need to be set for simulations using sparse grids. HyPar will automatically calculate the load balanced processor distribution for each sparse grid. If too many processors are specified, then it will return an error.
After running the code, there should be the following output files:
- op_fg_00000.dat, ..., op_fg_00010.dat: these contain the full grid solution at \(t=0, ..., 1\).
Since write_sg_solutions is set to no in sparse_grids.inp (SparseGridsSimulation::m_write_sg_solutions), sparse grid solution files are not written out.
Since HyPar::op_overwrite is set to no in solver.inp, separate files are written for solutions at each output time.
HyPar::op_file_format is set to tecplot2d in solver.inp, and thus, all the files are in a format that Tecplot (http://www.tecplot.com/) or other visualization software supporting the Tecplot format (e.g. VisIt - https://wci.llnl.gov/simulation/computer-codes/visit/) can read. In these files, the first two lines are the Tecplot headers, after which the data is written out as: the first two columns are grid indices, the next two columns are x and y coordinates, and the remaining columns are the solution components. HyPar::op_file_format can be set to text to get the solution files in plain text format (which can be read in and visualized in MATLAB for example).
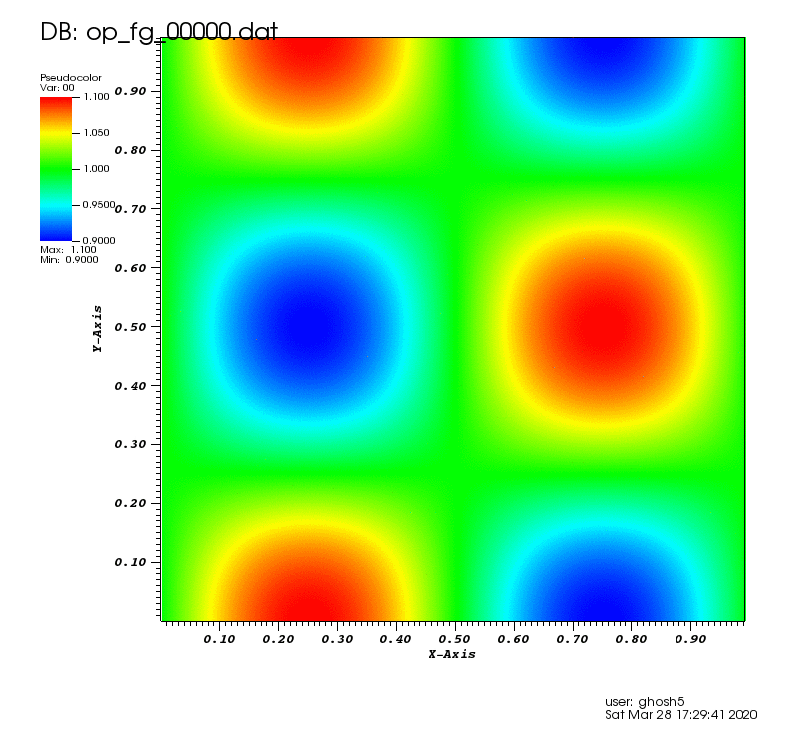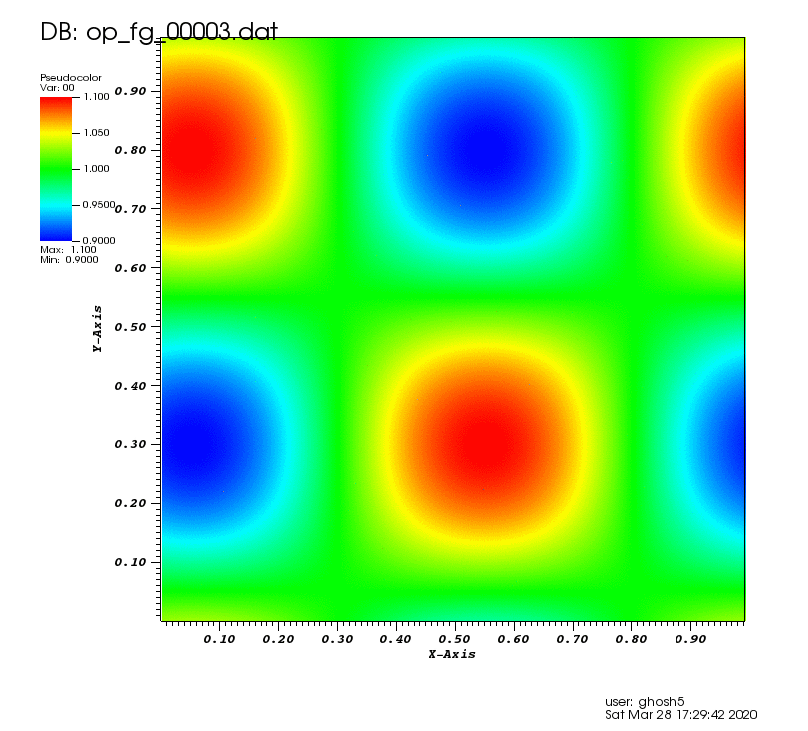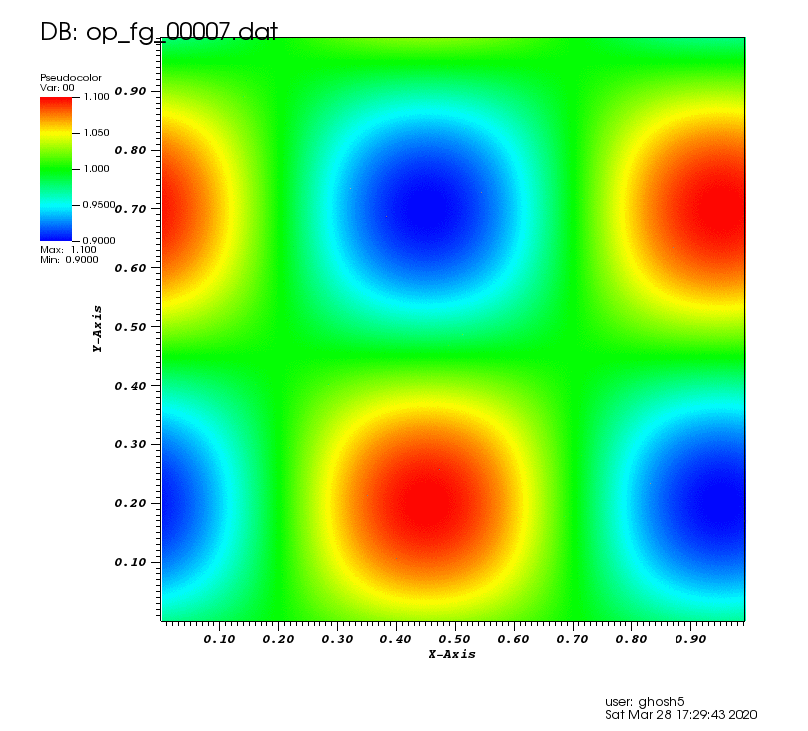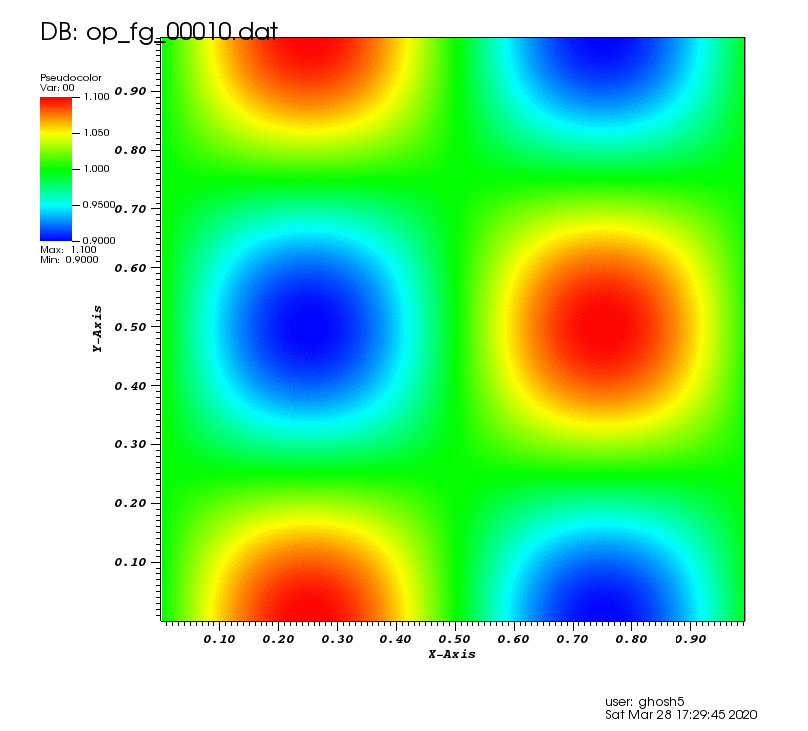
The following animation shows the density contours as the vortex convects over the domain:,
Since the exact solution is available at the final time, the numerical errors are calculated for the recombined full grid solution and reported on screen (see below) as well as errors_fg.dat:
128 128 4 2 2.5000000000000001E-03 2.2655211257995592E-09 2.2222058428741524E-09 1.9613330541637245E-09 6.7374190000000000E+00 6.8081639999999997E+00
The numbers are: number of grid points in each dimension (HyPar::dim_global), number of processors in each dimension (MPIVariables::iproc), time step size (HyPar::dt), L1, L2, and L-infinity errors (HyPar::error), solver wall time (seconds) (i.e., not accounting for initialization, and cleaning up), and total wall time.
Since write_sg_errors is set to to no in sparse_grids.inp (SparseGridsSimulation::m_print_sg_errors), the errors for each of the sparse grids are not computed or reported.
Expected screen output:
HyPar - Parallel (MPI) version with 8 processes
Compiled with PETSc time integration.
-- Sparse Grids Simulation --
Sparse grids inputs:
log2 of minimum grid size: 3
interpolation order: 6
write sparse grids solutions? no
Allocated full grid simulation object(s).
Reading solver inputs from file "solver.inp".
No. of dimensions : 2
No. of variables : 4
Domain size : 128 128
Processes along each dimension : 4 2
No. of ghosts pts : 3
No. of iter. : 400
Restart iteration : 0
Time integration scheme : rk (44)
Spatial discretization scheme (hyperbolic) : cupw5
Split hyperbolic flux term? : no
Interpolation type for hyperbolic term : components
Spatial discretization type (parabolic ) : nonconservative-2stage
Spatial discretization scheme (parabolic ) : 4
Time Step : 2.500000E-03
Check for conservation : no
Screen output iterations : 10
File output iterations : 40
Initial solution file type : binary
Initial solution read mode : serial
Solution file write mode : serial
Solution file format : tecplot2d
Overwrite solution file : no
Physical model : navierstokes2d
Processor distribution for full grid object: 4 2
Initializing sparse grids...
Number of spatial dimensions: 2
Computing sparse grids dimensions...
Number of sparse grid domains in combination technique: 9
Computing processor decompositions...
Sparse Grids: Combination technique grids sizes and coefficients are:-
0: dim = ( 128 8 ), coeff = +1.00e+00, iproc = ( 8 1 )
1: dim = ( 64 16 ), coeff = +1.00e+00, iproc = ( 8 1 )
2: dim = ( 32 32 ), coeff = +1.00e+00, iproc = ( 4 2 )
3: dim = ( 16 64 ), coeff = +1.00e+00, iproc = ( 1 8 )
4: dim = ( 8 128 ), coeff = +1.00e+00, iproc = ( 1 8 )
5: dim = ( 64 8 ), coeff = -1.00e+00, iproc = ( 8 1 )
6: dim = ( 32 16 ), coeff = -1.00e+00, iproc = ( 4 2 )
7: dim = ( 16 32 ), coeff = -1.00e+00, iproc = ( 2 4 )
8: dim = ( 8 64 ), coeff = -1.00e+00, iproc = ( 1 8 )
Allocating data arrays for full grid.
Partitioning domain and allocating data arrays.
Reading array from binary file initial.inp (Serial mode).
Volume integral of the initial solution:
0: 1.0000000000000000E+00
1: 1.0000000000000000E+00
2: 1.0000000000000000E+00
3: 2.7857142857142900E+00
Interpolating grid coordinates to sparse grids domain 0.
Interpolating grid coordinates to sparse grids domain 1.
Interpolating grid coordinates to sparse grids domain 2.
Interpolating grid coordinates to sparse grids domain 3.
Interpolating grid coordinates to sparse grids domain 4.
Interpolating grid coordinates to sparse grids domain 5.
Interpolating grid coordinates to sparse grids domain 6.
Interpolating grid coordinates to sparse grids domain 7.
Interpolating grid coordinates to sparse grids domain 8.
Domain 0: Reading boundary conditions from boundary.inp.
Boundary periodic: Along dimension 0 and face +1
Boundary periodic: Along dimension 0 and face -1
Boundary periodic: Along dimension 1 and face +1
Boundary periodic: Along dimension 1 and face -1
4 boundary condition(s) read.
Domain 1: Reading boundary conditions from boundary.inp.
Boundary periodic: Along dimension 0 and face +1
Boundary periodic: Along dimension 0 and face -1
Boundary periodic: Along dimension 1 and face +1
Boundary periodic: Along dimension 1 and face -1
4 boundary condition(s) read.
Domain 2: Reading boundary conditions from boundary.inp.
Boundary periodic: Along dimension 0 and face +1
Boundary periodic: Along dimension 0 and face -1
Boundary periodic: Along dimension 1 and face +1
Boundary periodic: Along dimension 1 and face -1
4 boundary condition(s) read.
Domain 3: Reading boundary conditions from boundary.inp.
Boundary periodic: Along dimension 0 and face +1
Boundary periodic: Along dimension 0 and face -1
Boundary periodic: Along dimension 1 and face +1
Boundary periodic: Along dimension 1 and face -1
4 boundary condition(s) read.
Domain 4: Reading boundary conditions from boundary.inp.
Boundary periodic: Along dimension 0 and face +1
Boundary periodic: Along dimension 0 and face -1
Boundary periodic: Along dimension 1 and face +1
Boundary periodic: Along dimension 1 and face -1
4 boundary condition(s) read.
Domain 5: Reading boundary conditions from boundary.inp.
Boundary periodic: Along dimension 0 and face +1
Boundary periodic: Along dimension 0 and face -1
Boundary periodic: Along dimension 1 and face +1
Boundary periodic: Along dimension 1 and face -1
4 boundary condition(s) read.
Domain 6: Reading boundary conditions from boundary.inp.
Boundary periodic: Along dimension 0 and face +1
Boundary periodic: Along dimension 0 and face -1
Boundary periodic: Along dimension 1 and face +1
Boundary periodic: Along dimension 1 and face -1
4 boundary condition(s) read.
Domain 7: Reading boundary conditions from boundary.inp.
Boundary periodic: Along dimension 0 and face +1
Boundary periodic: Along dimension 0 and face -1
Boundary periodic: Along dimension 1 and face +1
Boundary periodic: Along dimension 1 and face -1
4 boundary condition(s) read.
Domain 8: Reading boundary conditions from boundary.inp.
Boundary periodic: Along dimension 0 and face +1
Boundary periodic: Along dimension 0 and face -1
Boundary periodic: Along dimension 1 and face +1
Boundary periodic: Along dimension 1 and face -1
4 boundary condition(s) read.
Initializing solvers.
Initializing physics. Model = "navierstokes2d"
Reading physical model inputs from file "physics.inp".
Interpolating initial solution to sparse grids domain 0.
Volume integral of the initial solution on sparse grids domain 0:
0: 1.0000000000000000E+00
1: 1.0000000000000000E+00
2: 1.0000000000000000E+00
3: 2.7857142857142865E+00
Interpolating initial solution to sparse grids domain 1.
Volume integral of the initial solution on sparse grids domain 1:
0: 1.0000000000000000E+00
1: 1.0000000000000000E+00
2: 1.0000000000000000E+00
3: 2.7857142857142865E+00
Interpolating initial solution to sparse grids domain 2.
Volume integral of the initial solution on sparse grids domain 2:
0: 9.9999999999999989E-01
1: 9.9999999999999989E-01
2: 9.9999999999999989E-01
3: 2.7857142857142865E+00
Interpolating initial solution to sparse grids domain 3.
Volume integral of the initial solution on sparse grids domain 3:
0: 1.0000000000000000E+00
1: 1.0000000000000000E+00
2: 1.0000000000000000E+00
3: 2.7857142857142865E+00
Interpolating initial solution to sparse grids domain 4.
Volume integral of the initial solution on sparse grids domain 4:
0: 1.0000000000000000E+00
1: 1.0000000000000000E+00
2: 1.0000000000000000E+00
3: 2.7857142857142865E+00
Interpolating initial solution to sparse grids domain 5.
Volume integral of the initial solution on sparse grids domain 5:
0: 1.0000000000000000E+00
1: 1.0000000000000000E+00
2: 1.0000000000000000E+00
3: 2.7857142857142865E+00
Interpolating initial solution to sparse grids domain 6.
Volume integral of the initial solution on sparse grids domain 6:
0: 1.0000000000000000E+00
1: 1.0000000000000000E+00
2: 1.0000000000000000E+00
3: 2.7857142857142865E+00
Interpolating initial solution to sparse grids domain 7.
Volume integral of the initial solution on sparse grids domain 7:
0: 1.0000000000000000E+00
1: 1.0000000000000000E+00
2: 1.0000000000000000E+00
3: 2.7857142857142865E+00
Interpolating initial solution to sparse grids domain 8.
Volume integral of the initial solution on sparse grids domain 8:
0: 1.0000000000000000E+00
1: 1.0000000000000000E+00
2: 1.0000000000000000E+00
3: 2.7857142857142856E+00
Setting up time integration.
Solving in time (from 0 to 400 iterations)
Writing solution file op_fg_00000.dat.
--
Iteration: 10, Time: 2.500e-02
Max CFL: 3.284E-01, Max Diff. No.: -1.000E+00, Norm: 2.2212E-03
--
--
Iteration: 20, Time: 5.000e-02
Max CFL: 3.286E-01, Max Diff. No.: -1.000E+00, Norm: 2.2211E-03
--
--
Iteration: 30, Time: 7.500e-02
Max CFL: 3.286E-01, Max Diff. No.: -1.000E+00, Norm: 2.2209E-03
--
--
Iteration: 40, Time: 1.000e-01
Max CFL: 3.284E-01, Max Diff. No.: -1.000E+00, Norm: 2.2208E-03
--
Writing solution file op_fg_00001.dat.
--
Iteration: 50, Time: 1.250e-01
Max CFL: 3.280E-01, Max Diff. No.: -1.000E+00, Norm: 2.2207E-03
--
--
Iteration: 60, Time: 1.500e-01
Max CFL: 3.284E-01, Max Diff. No.: -1.000E+00, Norm: 2.2206E-03
--
--
Iteration: 70, Time: 1.750e-01
Max CFL: 3.286E-01, Max Diff. No.: -1.000E+00, Norm: 2.2204E-03
--
--
Iteration: 80, Time: 2.000e-01
Max CFL: 3.286E-01, Max Diff. No.: -1.000E+00, Norm: 2.2203E-03
--
Writing solution file op_fg_00002.dat.
--
Iteration: 90, Time: 2.250e-01
Max CFL: 3.284E-01, Max Diff. No.: -1.000E+00, Norm: 2.2202E-03
--
--
Iteration: 100, Time: 2.500e-01
Max CFL: 3.280E-01, Max Diff. No.: -1.000E+00, Norm: 2.2200E-03
--
--
Iteration: 110, Time: 2.750e-01
Max CFL: 3.284E-01, Max Diff. No.: -1.000E+00, Norm: 2.2199E-03
--
--
Iteration: 120, Time: 3.000e-01
Max CFL: 3.286E-01, Max Diff. No.: -1.000E+00, Norm: 2.2197E-03
--
Writing solution file op_fg_00003.dat.
--
Iteration: 130, Time: 3.250e-01
Max CFL: 3.286E-01, Max Diff. No.: -1.000E+00, Norm: 2.2196E-03
--
--
Iteration: 140, Time: 3.500e-01
Max CFL: 3.284E-01, Max Diff. No.: -1.000E+00, Norm: 2.2195E-03
--
--
Iteration: 150, Time: 3.750e-01
Max CFL: 3.280E-01, Max Diff. No.: -1.000E+00, Norm: 2.2193E-03
--
--
Iteration: 160, Time: 4.000e-01
Max CFL: 3.284E-01, Max Diff. No.: -1.000E+00, Norm: 2.2192E-03
--
Writing solution file op_fg_00004.dat.
--
Iteration: 170, Time: 4.250e-01
Max CFL: 3.286E-01, Max Diff. No.: -1.000E+00, Norm: 2.2190E-03
--
--
Iteration: 180, Time: 4.500e-01
Max CFL: 3.286E-01, Max Diff. No.: -1.000E+00, Norm: 2.2189E-03
--
--
Iteration: 190, Time: 4.750e-01
Max CFL: 3.284E-01, Max Diff. No.: -1.000E+00, Norm: 2.2188E-03
--
--
Iteration: 200, Time: 5.000e-01
Max CFL: 3.280E-01, Max Diff. No.: -1.000E+00, Norm: 2.2186E-03
--
Writing solution file op_fg_00005.dat.
--
Iteration: 210, Time: 5.250e-01
Max CFL: 3.284E-01, Max Diff. No.: -1.000E+00, Norm: 2.2185E-03
--
--
Iteration: 220, Time: 5.500e-01
Max CFL: 3.286E-01, Max Diff. No.: -1.000E+00, Norm: 2.2184E-03
--
--
Iteration: 230, Time: 5.750e-01
Max CFL: 3.286E-01, Max Diff. No.: -1.000E+00, Norm: 2.2182E-03
--
--
Iteration: 240, Time: 6.000e-01
Max CFL: 3.284E-01, Max Diff. No.: -1.000E+00, Norm: 2.2181E-03
--
Writing solution file op_fg_00006.dat.
--
Iteration: 250, Time: 6.250e-01
Max CFL: 3.279E-01, Max Diff. No.: -1.000E+00, Norm: 2.2179E-03
--
--
Iteration: 260, Time: 6.500e-01
Max CFL: 3.284E-01, Max Diff. No.: -1.000E+00, Norm: 2.2178E-03
--
--
Iteration: 270, Time: 6.750e-01
Max CFL: 3.286E-01, Max Diff. No.: -1.000E+00, Norm: 2.2177E-03
--
--
Iteration: 280, Time: 7.000e-01
Max CFL: 3.286E-01, Max Diff. No.: -1.000E+00, Norm: 2.2175E-03
--
Writing solution file op_fg_00007.dat.
--
Iteration: 290, Time: 7.250e-01
Max CFL: 3.284E-01, Max Diff. No.: -1.000E+00, Norm: 2.2174E-03
--
--
Iteration: 300, Time: 7.500e-01
Max CFL: 3.279E-01, Max Diff. No.: -1.000E+00, Norm: 2.2173E-03
--
--
Iteration: 310, Time: 7.750e-01
Max CFL: 3.284E-01, Max Diff. No.: -1.000E+00, Norm: 2.2171E-03
--
--
Iteration: 320, Time: 8.000e-01
Max CFL: 3.286E-01, Max Diff. No.: -1.000E+00, Norm: 2.2170E-03
--
Writing solution file op_fg_00008.dat.
--
Iteration: 330, Time: 8.250e-01
Max CFL: 3.286E-01, Max Diff. No.: -1.000E+00, Norm: 2.2168E-03
--
--
Iteration: 340, Time: 8.500e-01
Max CFL: 3.283E-01, Max Diff. No.: -1.000E+00, Norm: 2.2167E-03
--
--
Iteration: 350, Time: 8.750e-01
Max CFL: 3.279E-01, Max Diff. No.: -1.000E+00, Norm: 2.2166E-03
--
--
Iteration: 360, Time: 9.000e-01
Max CFL: 3.284E-01, Max Diff. No.: -1.000E+00, Norm: 2.2164E-03
--
Writing solution file op_fg_00009.dat.
--
Iteration: 370, Time: 9.250e-01
Max CFL: 3.286E-01, Max Diff. No.: -1.000E+00, Norm: 2.2163E-03
--
--
Iteration: 380, Time: 9.500e-01
Max CFL: 3.286E-01, Max Diff. No.: -1.000E+00, Norm: 2.2161E-03
--
--
Iteration: 390, Time: 9.750e-01
Max CFL: 3.283E-01, Max Diff. No.: -1.000E+00, Norm: 2.2160E-03
--
--
Iteration: 400, Time: 1.000e+00
Max CFL: 3.280E-01, Max Diff. No.: -1.000E+00, Norm: 2.2159E-03
--
Writing solution file op_fg_00010.dat.
Completed time integration (Final time: 1.000000).
Reading array from binary file exact.inp (Serial mode).
Computed errors for full grid solution:
L1 Error: 2.2655211257995592E-09
L2 Error: 2.2222058428741524E-09
Linf Error: 1.9613330541637245E-09
Solver runtime (in seconds): 6.7374190000000000E+00
Total runtime (in seconds): 6.8081639999999997E+00
Deallocating arrays.
Finished.