2D Euler Equations - Isentropic Vortex Convection
See 2D Euler Equations - Isentropic Vortex Convection to familiarize yourself with this case.
Location: hypar/Examples/2D/NavierStokes2D/InviscidVortexConvection_libROM_DMD_Train (This directory contains all the input files needed to run this case.)
Governing equations: 2D Euler Equations (navierstokes2d.h - By default, NavierStokes2D::Re is set to -1 which makes the code skip the parabolic terms, i.e., the 2D Euler equations are solved.)
Reduced Order Modeling: This example trains a DMD object and then predicts the solution using the DMD at the same times that the actual HyPar solution is written at.
Reference: C.-W. Shu, "Essentially Non-oscillatory and Weighted Essentially Non-oscillatory Schemes for Hyperbolic Conservation Laws", ICASE Report 97-65, 1997
Domain: \(0 \le x,y \le 10\), "periodic" (_PERIODIC_) boundary conditions.
Initial solution: The freestream flow is given by
\begin{equation} \rho_\infty = 1,\ u_\infty = 0.1,\ v_\infty = 0,\ p_\infty = 1 \end{equation}
and a vortex is introduced, specified as
\begin{align} \rho &= \left[ 1 - \frac{\left(\gamma-1\right)b^2}{8\gamma\pi^2} e^{1-r^2} \right]^{\frac{1}{\gamma-1}},\ p = \rho^\gamma, \\ u &= u_\infty - \frac{b}{2\pi} e^{\frac{1}{2}\left(1-r^2\right)} \left(y-y_c\right),\ v = v_\infty + \frac{b}{2\pi} e^{\frac{1}{2}\left(1-r^2\right)} \left(x-x_c\right), \end{align}
where \(b=0.5\) is the vortex strength and \(r = \left[(x-x_c)^2 + (y-y_c)^2 \right]^{1/2}\) is the distance from the vortex center \(\left(x_c,y_c\right) = \left(5,5\right)\).
Numerical method:
- Spatial discretization (hyperbolic): 5th order CRWENO (Interp1PrimFifthOrderCRWENO())
- Time integration: SSPRK3 (TimeRK(), _RK_SSP3_)
Reduced Order Modeling:
- Mode: train (libROMInterface::m_mode, _ROM_MODE_TRAIN_)
- Component Mode: monolithic (libROMInterface::m_comp_mode, _ROM_COMP_MODE_MONOLITHIC_)
- Type: Dynamic Mode Decomposition (DMD) with time windowing (libROMInterface::m_rom_type)
- Latent subspace dimension: 16 (DMDROMObject::m_rdim)
Input files required:
librom.inp
begin
rdim 16
sampling_frequency 1
mode train
end
solver.inp
begin
ndims 2
nvars 4
size 64 64
iproc 4 4
ghost 3
n_iter 800
restart_iter 0
time_scheme rk
time_scheme_type ssprk3
hyp_space_scheme crweno5
hyp_flux_split no
hyp_interp_type components
par_space_type nonconservative-2stage
par_space_scheme 4
dt 0.025
conservation_check yes
screen_op_iter 20
file_op_iter 40
input_mode serial
ip_file_type binary
output_mode serial
op_file_format binary
op_overwrite no
model navierstokes2d
end
boundary.inp
4
periodic 0 1 0 0 0 10.0
periodic 0 -1 0 0 0 10.0
periodic 1 1 0 10.0 0 0
periodic 1 -1 0 10.0 0 0
physics.inp
begin
gamma 1.4
upwinding roe
end
weno.inp (optional)
begin
mapped 1
borges 0
yc 0
no_limiting 0
epsilon 0.000001
p 2.0
rc 0.3
xi 0.001
end
lusolver.inp (optional)
begin
reducedsolvetype gather-and-solve
evaluate_norm 1
maxiter 10
atol 1e-12
rtol 1e-10
verbose 0
end
To generate initial.inp (initial solution) and exact.inp (exact solution), compile and run the following code in the run directory.
#include <stdio.h>
#include <stdlib.h>
#include <math.h>
#include <string.h>
double power(double x,double a)
{
return(exp(a*log(x)));
}
int main(){
const double pi = 4.0*atan(1.0);
const double GAMMA = 1.4;
int NI,NJ,ndims,n_iter;
double tf, dt;
char ip_file_type[50]; strcpy(ip_file_type,"ascii");
FILE *in, *out;
printf("Reading file \"solver.inp\"...\n");
in = fopen("solver.inp","r");
if (!in) {
printf("Error: Input file \"solver.inp\" not found. Default values will be used.\n");
return(0);
} else {
char word[500];
fscanf(in,"%s",word);
if (!strcmp(word, "begin")) {
while (strcmp(word, "end")) {
fscanf(in,"%s",word);
if (!strcmp(word, "ndims")) fscanf(in,"%d",&ndims);
else if (!strcmp(word, "size")) {
fscanf(in,"%d",&NI);
fscanf(in,"%d",&NJ);
} else if (!strcmp(word, "n_iter")) fscanf(in,"%d",&n_iter);
else if (!strcmp(word, "dt")) fscanf(in,"%lf",&dt);
else if (!strcmp(word, "ip_file_type")) fscanf(in,"%s",ip_file_type);
}
} else printf("Error: Illegal format in solver.inp. Crash and burn!\n");
}
fclose(in);
if (ndims != 2) {
printf("ndims is not 2 in solver.inp. this code is to generate 2D exact solution\n");
return(0);
}
printf("Grid:\t\t\t%d X %d\n",NI,NJ);
int i,j;
double dx = 10.0 / ((double)NI);
double dy = 10.0 / ((double)NJ);
tf = (double)n_iter * dt; double tff = tf;
while (tf > 20) tf -= 20; // Time period
double *x, *y, *u0, *u1, *u2, *u3;
x = (double*) calloc (NI , sizeof(double));
y = (double*) calloc (NJ , sizeof(double));
u0 = (double*) calloc (NI*NJ, sizeof(double));
u1 = (double*) calloc (NI*NJ, sizeof(double));
u2 = (double*) calloc (NI*NJ, sizeof(double));
u3 = (double*) calloc (NI*NJ, sizeof(double));
double u_inf = 0.5;
double v_inf = 0.0;
double b = u_inf;
double x0, y0;
/* Initial solution */
x0 = 5.0, y0 = 5.0;
for (i = 0; i < NI; i++){
for (j = 0; j < NJ; j++){
x[i] = i*dx;
y[j] = j*dy;
int p = NJ*i + j;
double rx, ry;
rx = (x[i] - x0);
ry = (y[j] - y0);
if (rx < -5) { rx += 10; }
else if (rx > 5) { rx -= 10; }
double rsq = rx*rx + ry*ry;
double rho, u, v, P;
double du, dv;
rho = power(1.0 - ((GAMMA-1.0)*b*b)/(8.0*GAMMA*pi*pi) * exp(1.0-rsq), 1.0/(GAMMA-1.0));
P = power(rho,GAMMA);
du = - b/(2.0*pi) * exp(0.5*(1.0-rsq)) * ry;
dv = b/(2.0*pi) * exp(0.5*(1.0-rsq)) * rx;
u = u_inf + du;
v = v_inf + dv;
u0[p] = rho;
u1[p] = rho*u;
u2[p] = rho*v;
u3[p] = P/(GAMMA-1.0) + 0.5*rho*(u*u+v*v);
}
}
if (!strcmp(ip_file_type,"ascii")) {
printf("Writing ASCII initial solution file initial.inp\n");
out = fopen("initial.inp","w");
for (i = 0; i < NI; i++) fprintf(out,"%lf ",x[i]);
fprintf(out,"\n");
for (j = 0; j < NJ; j++) fprintf(out,"%lf ",y[j]);
fprintf(out,"\n");
for (j = 0; j < NJ; j++) {
for (i = 0; i < NI; i++) {
int p = NJ*i + j;
fprintf(out,"%lf ",u0[p]);
}
}
fprintf(out,"\n");
for (j = 0; j < NJ; j++) {
for (i = 0; i < NI; i++) {
int p = NJ*i + j;
fprintf(out,"%lf ",u1[p]);
}
}
fprintf(out,"\n");
for (j = 0; j < NJ; j++) {
for (i = 0; i < NI; i++) {
int p = NJ*i + j;
fprintf(out,"%lf ",u2[p]);
}
}
fprintf(out,"\n");
for (j = 0; j < NJ; j++) {
for (i = 0; i < NI; i++) {
int p = NJ*i + j;
fprintf(out,"%lf ",u3[p]);
}
}
fprintf(out,"\n");
fclose(out);
} else if ((!strcmp(ip_file_type,"binary")) || (!strcmp(ip_file_type,"bin"))) {
printf("Writing binary initial solution file initial.inp\n");
out = fopen("initial.inp","wb");
fwrite(x,sizeof(double),NI,out);
fwrite(y,sizeof(double),NJ,out);
double *U = (double*) calloc (4*NI*NJ,sizeof(double));
for (i=0; i < NI; i++) {
for (j = 0; j < NJ; j++) {
int p = NJ*i + j;
int q = NI*j + i;
U[4*q+0] = u0[p];
U[4*q+1] = u1[p];
U[4*q+2] = u2[p];
U[4*q+3] = u3[p];
}
}
fwrite(U,sizeof(double),4*NI*NJ,out);
free(U);
fclose(out);
}
/* Exact solution */
x0 = 5.0+tf*u_inf, y0 = 5.0;
if (x0 > 10) x0 -= 10; //periodic domain
printf("Final time: %lf, Vortex center: %lf, %lf\n",tff,x0,y0);
for (i = 0; i < NI; i++){
for (j = 0; j < NJ; j++){
x[i] = i*dx;
y[j] = j*dy;
int p = NJ*i + j;
double rx, ry;
rx = (x[i] - x0);
ry = (y[j] - y0);
if (rx < -5) { rx += 10; }
else if (rx > 5) { rx -= 10; }
double rsq = rx*rx + ry*ry;
double rho, u, v, P;
double du, dv;
rho = power(1.0 - ((GAMMA-1.0)*b*b)/(8.0*GAMMA*pi*pi) * exp(1.0-rsq), 1.0/(GAMMA-1.0));
P = power(rho,GAMMA);
du = - b/(2.0*pi) * exp(0.5*(1.0-rsq)) * ry;
dv = b/(2.0*pi) * exp(0.5*(1.0-rsq)) * rx;
u = u_inf + du;
v = v_inf + dv;
u0[p] = rho;
u1[p] = rho*u;
u2[p] = rho*v;
u3[p] = P/(GAMMA-1.0) + 0.5*rho*(u*u+v*v);
}
}
if (!strcmp(ip_file_type,"ascii")) {
printf("Writing ASCII exact solution file exact.inp\n");
out = fopen("exact.inp","w");
for (i = 0; i < NI; i++) fprintf(out,"%lf ",x[i]);
fprintf(out,"\n");
for (j = 0; j < NJ; j++) fprintf(out,"%lf ",y[j]);
fprintf(out,"\n");
for (j = 0; j < NJ; j++) {
for (i = 0; i < NI; i++) {
int p = NJ*i + j;
fprintf(out,"%lf ",u0[p]);
}
}
fprintf(out,"\n");
for (j = 0; j < NJ; j++) {
for (i = 0; i < NI; i++) {
int p = NJ*i + j;
fprintf(out,"%lf ",u1[p]);
}
}
fprintf(out,"\n");
for (j = 0; j < NJ; j++) {
for (i = 0; i < NI; i++) {
int p = NJ*i + j;
fprintf(out,"%lf ",u2[p]);
}
}
fprintf(out,"\n");
for (j = 0; j < NJ; j++) {
for (i = 0; i < NI; i++) {
int p = NJ*i + j;
fprintf(out,"%lf ",u3[p]);
}
}
fprintf(out,"\n");
fclose(out);
} else if ((!strcmp(ip_file_type,"binary")) || (!strcmp(ip_file_type,"bin"))) {
printf("Writing binary exact solution file exact.inp\n");
out = fopen("exact.inp","wb");
fwrite(x,sizeof(double),NI,out);
fwrite(y,sizeof(double),NJ,out);
double *U = (double*) calloc (4*NI*NJ,sizeof(double));
for (i=0; i < NI; i++) {
for (j = 0; j < NJ; j++) {
int p = NJ*i + j;
int q = NI*j + i;
U[4*q+0] = u0[p];
U[4*q+1] = u1[p];
U[4*q+2] = u2[p];
U[4*q+3] = u3[p];
}
}
fwrite(U,sizeof(double),4*NI*NJ,out);
free(U);
fclose(out);
}
free(x);
free(y);
free(u0);
free(u1);
free(u2);
free(u3);
return(0);
}
Output:
Note that iproc is set to
4 4
in solver.inp (i.e., 4 processors along x, and 4 processors along y). Thus, this example should be run with 16 MPI ranks (or change iproc).
After running the code, there should be the following output files:
- 21 output files op_00000.bin, op_00001.bin, ... op_00020.bin; these are the HyPar solutions.
- 21 output files op_rom_00000.bin, op_rom_00001.bin, ... op_rom_00020.bin; these are the predicted solutions from the DMD object(s).
The first of each of these file sets is the solution at \(t=0\) and the final one is the solution at \(t=20\). Since HyPar::op_overwrite is set to no in solver.inp, a separate file is written for solutions at each output time. All the files are binary (HyPar::op_file_format is set to binary in solver.inp).
The provided Python script (plotSolution.py) can be used to generate plots from the binary files that compare the HyPar and DMD solutions. Alternatively, HyPar::op_file_format can be set to tecplot2d, and Tecplot/VisIt or something similar can be used to plot the resulting files.
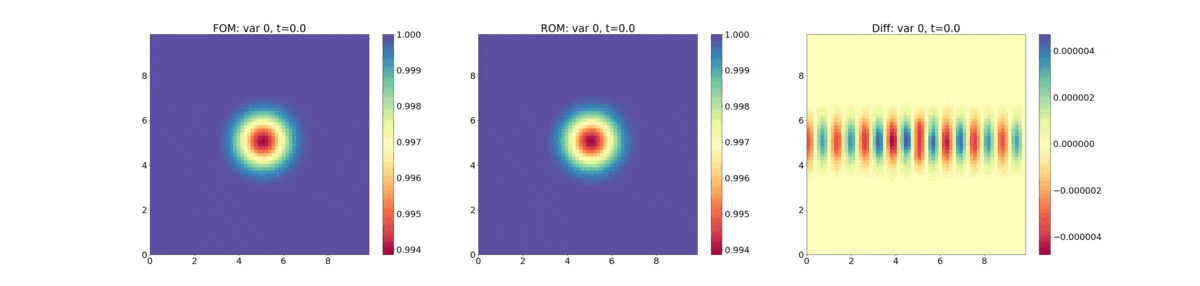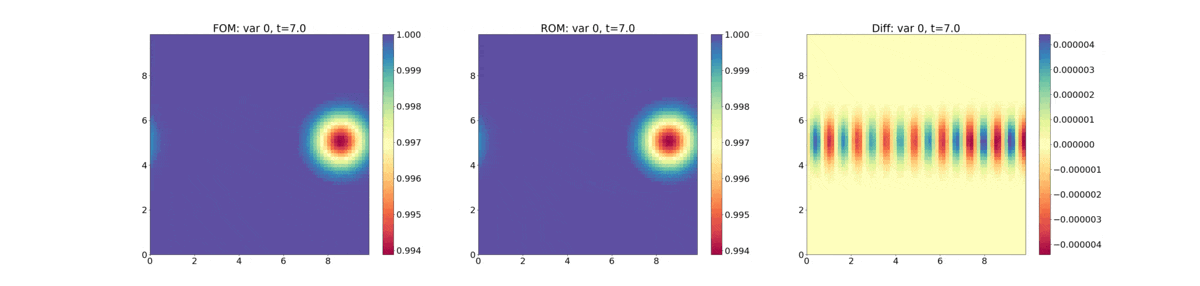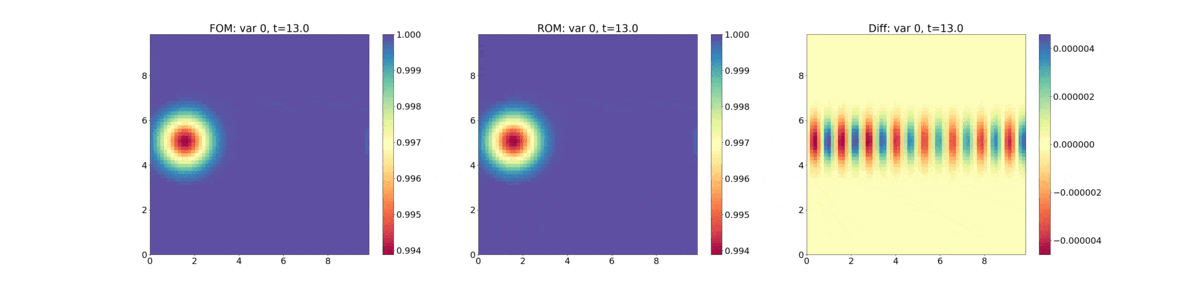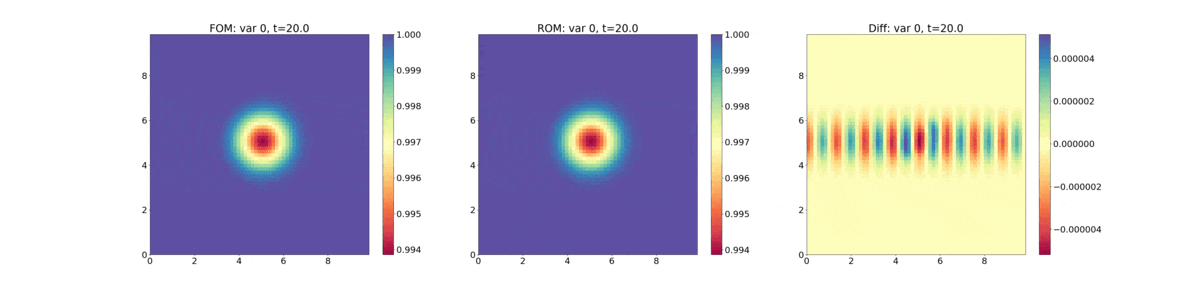
The following plot shows evolution of the density - FOM (full-order model) refers to the HyPar solution, ROM (reduced-order model) refers to the DMD solution, and "Diff" is their difference.
Wall clock times:
- PDE solution: 5.85 seconds
- DMD training time: 5.25 seconds
- DMD prediction/query time: 0.28 seconds
The L1, L2, and Linf norms of the diff between the HyPar and ROM solution at the final time are calculated and reported on screen (see below) as well as pde_rom_diff.dat:
64 64 4 4 2.5000000000000001E-02 1.5215990100709741E-06 4.0657029052378237E-06 2.1594369212267493E-05 1.5002807000000001E+01 1.5717855999999999E+01
The numbers are: number of grid points in each dimension (HyPar::dim_global), number of processors in each dimension (MPIVariables::iproc), time step size (HyPar::dt), L1, L2, and L-infinity norms of the diff (HyPar::rom_diff_norms), solver wall time (seconds) (i.e., not accounting for initialization, and cleaning up), and total wall time.
By default, the code will write the trained DMD object(s) to files in a subdirectory (DMDROMObject::m_dirname - default value is "DMD"). If the subdirectory does not exist, the code may not report an error (or give some HDF5 file-writing error); the DMD objects will not be written! If the subdirectory exists, several files will exist after the simulation is complete - they are in a format that is readable by libROM.
Expected screen output:
HyPar - Parallel (MPI) version with 16 processes
Compiled with PETSc time integration.
Allocated simulation object(s).
Reading solver inputs from file "solver.inp".
No. of dimensions : 2
No. of variables : 4
Domain size : 64 64
Processes along each dimension : 4 4
Exact solution domain size : 64 64
No. of ghosts pts : 3
No. of iter. : 800
Restart iteration : 0
Time integration scheme : rk (ssprk3)
Spatial discretization scheme (hyperbolic) : crweno5
Split hyperbolic flux term? : no
Interpolation type for hyperbolic term : components
Spatial discretization type (parabolic ) : nonconservative-2stage
Spatial discretization scheme (parabolic ) : 4
Time Step : 2.500000E-02
Check for conservation : yes
Screen output iterations : 20
File output iterations : 40
Initial solution file type : binary
Initial solution read mode : serial
Solution file write mode : serial
Solution file format : binary
Overwrite solution file : no
Physical model : navierstokes2d
Partitioning domain and allocating data arrays.
Reading array from binary file initial.inp (Serial mode).
Volume integral of the initial solution:
0: 9.9980704056028685E+01
1: 4.9990352985508352E+01
2: -9.5749398777884853E-07
3: 2.6245709189715654E+02
Reading boundary conditions from boundary.inp.
Boundary periodic: Along dimension 0 and face +1
Boundary periodic: Along dimension 0 and face -1
Boundary periodic: Along dimension 1 and face +1
Boundary periodic: Along dimension 1 and face -1
4 boundary condition(s) read.
Initializing solvers.
Reading WENO parameters from weno.inp.
Initializing physics. Model = "navierstokes2d"
Reading physical model inputs from file "physics.inp".
Setting up time integration.
Setting up libROM interface.
libROM inputs and parameters:
reduced model dimensionality: 16
sampling frequency: 1
mode: train
type: DMD
save to file: true
local vector size: 1024
libROM DMD inputs:
number of samples per window: 2147483647
directory name for DMD onjects: DMD
Solving in time (from 0 to 800 iterations)
Writing solution file op_00000.bin.
DMDROMObject::takeSample() - creating new DMD object, t=0.000000 (total: 1).
iter= 20 t=5.000E-01 CFL=2.819E-01 norm=3.0130E-04 wctime: 7.5E-03 (s) cons_err=3.6443E-16
iter= 40 t=1.000E+00 CFL=2.819E-01 norm=3.0130E-04 wctime: 7.4E-03 (s) cons_err=4.5731E-16
Writing solution file op_00001.bin.
iter= 60 t=1.500E+00 CFL=2.819E-01 norm=3.0130E-04 wctime: 7.4E-03 (s) cons_err=4.2677E-16
iter= 80 t=2.000E+00 CFL=2.819E-01 norm=3.0130E-04 wctime: 7.3E-03 (s) cons_err=3.8260E-16
Writing solution file op_00002.bin.
iter= 100 t=2.500E+00 CFL=2.819E-01 norm=3.0130E-04 wctime: 7.4E-03 (s) cons_err=5.4237E-16
iter= 120 t=3.000E+00 CFL=2.819E-01 norm=3.0130E-04 wctime: 7.4E-03 (s) cons_err=6.7929E-16
Writing solution file op_00003.bin.
iter= 140 t=3.500E+00 CFL=2.819E-01 norm=3.0130E-04 wctime: 7.3E-03 (s) cons_err=4.5072E-16
iter= 160 t=4.000E+00 CFL=2.819E-01 norm=3.0130E-04 wctime: 7.3E-03 (s) cons_err=4.8666E-16
Writing solution file op_00004.bin.
iter= 180 t=4.500E+00 CFL=2.819E-01 norm=3.0130E-04 wctime: 7.3E-03 (s) cons_err=4.2941E-16
iter= 200 t=5.000E+00 CFL=2.819E-01 norm=3.0130E-04 wctime: 7.3E-03 (s) cons_err=7.1598E-16
Writing solution file op_00005.bin.
iter= 220 t=5.500E+00 CFL=2.819E-01 norm=3.0129E-04 wctime: 7.3E-03 (s) cons_err=5.1671E-16
iter= 240 t=6.000E+00 CFL=2.819E-01 norm=3.0129E-04 wctime: 7.3E-03 (s) cons_err=5.6309E-16
Writing solution file op_00006.bin.
iter= 260 t=6.500E+00 CFL=2.819E-01 norm=3.0129E-04 wctime: 7.3E-03 (s) cons_err=8.0548E-16
iter= 280 t=7.000E+00 CFL=2.819E-01 norm=3.0129E-04 wctime: 7.3E-03 (s) cons_err=4.6018E-16
Writing solution file op_00007.bin.
iter= 300 t=7.500E+00 CFL=2.819E-01 norm=3.0129E-04 wctime: 7.3E-03 (s) cons_err=6.5184E-16
iter= 320 t=8.000E+00 CFL=2.819E-01 norm=3.0129E-04 wctime: 7.3E-03 (s) cons_err=7.5702E-16
Writing solution file op_00008.bin.
iter= 340 t=8.500E+00 CFL=2.819E-01 norm=3.0129E-04 wctime: 7.3E-03 (s) cons_err=6.2308E-16
iter= 360 t=9.000E+00 CFL=2.819E-01 norm=3.0129E-04 wctime: 7.3E-03 (s) cons_err=6.6669E-16
Writing solution file op_00009.bin.
iter= 380 t=9.500E+00 CFL=2.819E-01 norm=3.0129E-04 wctime: 7.3E-03 (s) cons_err=5.0268E-16
iter= 400 t=1.000E+01 CFL=2.819E-01 norm=3.0129E-04 wctime: 7.3E-03 (s) cons_err=8.3668E-16
Writing solution file op_00010.bin.
iter= 420 t=1.050E+01 CFL=2.819E-01 norm=3.0129E-04 wctime: 7.3E-03 (s) cons_err=7.7057E-16
iter= 440 t=1.100E+01 CFL=2.819E-01 norm=3.0129E-04 wctime: 7.3E-03 (s) cons_err=7.2270E-16
Writing solution file op_00011.bin.
iter= 460 t=1.150E+01 CFL=2.819E-01 norm=3.0129E-04 wctime: 7.3E-03 (s) cons_err=6.4813E-16
iter= 480 t=1.200E+01 CFL=2.819E-01 norm=3.0129E-04 wctime: 7.3E-03 (s) cons_err=7.7048E-16
Writing solution file op_00012.bin.
iter= 500 t=1.250E+01 CFL=2.819E-01 norm=3.0129E-04 wctime: 7.3E-03 (s) cons_err=6.7747E-16
iter= 520 t=1.300E+01 CFL=2.819E-01 norm=3.0129E-04 wctime: 7.3E-03 (s) cons_err=7.1146E-16
Writing solution file op_00013.bin.
iter= 540 t=1.350E+01 CFL=2.819E-01 norm=3.0129E-04 wctime: 7.3E-03 (s) cons_err=7.2240E-16
iter= 560 t=1.400E+01 CFL=2.819E-01 norm=3.0129E-04 wctime: 7.3E-03 (s) cons_err=4.3982E-16
Writing solution file op_00014.bin.
iter= 580 t=1.450E+01 CFL=2.819E-01 norm=3.0128E-04 wctime: 7.3E-03 (s) cons_err=6.1261E-16
iter= 600 t=1.500E+01 CFL=2.819E-01 norm=3.0128E-04 wctime: 7.3E-03 (s) cons_err=8.0060E-16
Writing solution file op_00015.bin.
iter= 620 t=1.550E+01 CFL=2.819E-01 norm=3.0128E-04 wctime: 7.3E-03 (s) cons_err=8.1379E-16
iter= 640 t=1.600E+01 CFL=2.819E-01 norm=3.0128E-04 wctime: 7.4E-03 (s) cons_err=1.0016E-15
Writing solution file op_00016.bin.
iter= 660 t=1.650E+01 CFL=2.819E-01 norm=3.0128E-04 wctime: 7.3E-03 (s) cons_err=7.6872E-16
iter= 680 t=1.700E+01 CFL=2.819E-01 norm=3.0128E-04 wctime: 7.3E-03 (s) cons_err=7.8560E-16
Writing solution file op_00017.bin.
iter= 700 t=1.750E+01 CFL=2.819E-01 norm=3.0128E-04 wctime: 7.3E-03 (s) cons_err=4.2793E-16
iter= 720 t=1.800E+01 CFL=2.819E-01 norm=3.0128E-04 wctime: 7.4E-03 (s) cons_err=6.7370E-16
Writing solution file op_00018.bin.
iter= 740 t=1.850E+01 CFL=2.819E-01 norm=3.0128E-04 wctime: 7.3E-03 (s) cons_err=4.6653E-16
iter= 760 t=1.900E+01 CFL=2.819E-01 norm=3.0128E-04 wctime: 7.3E-03 (s) cons_err=5.3238E-16
Writing solution file op_00019.bin.
iter= 780 t=1.950E+01 CFL=2.819E-01 norm=3.0128E-04 wctime: 7.4E-03 (s) cons_err=8.5277E-16
iter= 800 t=2.000E+01 CFL=2.819E-01 norm=3.0128E-04 wctime: 7.3E-03 (s) cons_err=1.0167E-15
Completed time integration (Final time: 20.000000), total wctime: 5.852587 (seconds).
Reading array from binary file exact.inp (Serial mode).
Writing solution file op_00020.bin.
libROM: Training ROM.
DMDROMObject::train() - training DMD object 0 with 800 samples.
Using 16 basis vectors out of 799.
libROM: total training wallclock time: 5.253873 (seconds).
libROM: Predicting solution at time 0.0000e+00 using ROM.
libROM: wallclock time: 0.013751 (seconds).
Writing solution file op_rom_00000.bin.
libROM: Predicting solution at time 1.0000e+00 using ROM.
libROM: wallclock time: 0.013635 (seconds).
Writing solution file op_rom_00001.bin.
libROM: Predicting solution at time 2.0000e+00 using ROM.
libROM: wallclock time: 0.013599 (seconds).
Writing solution file op_rom_00002.bin.
libROM: Predicting solution at time 3.0000e+00 using ROM.
libROM: wallclock time: 0.013555 (seconds).
Writing solution file op_rom_00003.bin.
libROM: Predicting solution at time 4.0000e+00 using ROM.
libROM: wallclock time: 0.013559 (seconds).
Writing solution file op_rom_00004.bin.
libROM: Predicting solution at time 5.0000e+00 using ROM.
libROM: wallclock time: 0.013557 (seconds).
Writing solution file op_rom_00005.bin.
libROM: Predicting solution at time 6.0000e+00 using ROM.
libROM: wallclock time: 0.013576 (seconds).
Writing solution file op_rom_00006.bin.
libROM: Predicting solution at time 7.0000e+00 using ROM.
libROM: wallclock time: 0.013567 (seconds).
Writing solution file op_rom_00007.bin.
libROM: Predicting solution at time 8.0000e+00 using ROM.
libROM: wallclock time: 0.013559 (seconds).
Writing solution file op_rom_00008.bin.
libROM: Predicting solution at time 9.0000e+00 using ROM.
libROM: wallclock time: 0.013639 (seconds).
Writing solution file op_rom_00009.bin.
libROM: Predicting solution at time 1.0000e+01 using ROM.
libROM: wallclock time: 0.013553 (seconds).
Writing solution file op_rom_00010.bin.
libROM: Predicting solution at time 1.1000e+01 using ROM.
libROM: wallclock time: 0.013556 (seconds).
Writing solution file op_rom_00011.bin.
libROM: Predicting solution at time 1.2000e+01 using ROM.
libROM: wallclock time: 0.013559 (seconds).
Writing solution file op_rom_00012.bin.
libROM: Predicting solution at time 1.3000e+01 using ROM.
libROM: wallclock time: 0.013558 (seconds).
Writing solution file op_rom_00013.bin.
libROM: Predicting solution at time 1.4000e+01 using ROM.
libROM: wallclock time: 0.013564 (seconds).
Writing solution file op_rom_00014.bin.
libROM: Predicting solution at time 1.5000e+01 using ROM.
libROM: wallclock time: 0.013554 (seconds).
Writing solution file op_rom_00015.bin.
libROM: Predicting solution at time 1.6000e+01 using ROM.
libROM: wallclock time: 0.013560 (seconds).
Writing solution file op_rom_00016.bin.
libROM: Predicting solution at time 1.7000e+01 using ROM.
libROM: wallclock time: 0.013558 (seconds).
Writing solution file op_rom_00017.bin.
libROM: Predicting solution at time 1.8000e+01 using ROM.
libROM: wallclock time: 0.013559 (seconds).
Writing solution file op_rom_00018.bin.
libROM: Predicting solution at time 1.9000e+01 using ROM.
libROM: wallclock time: 0.013564 (seconds).
Writing solution file op_rom_00019.bin.
libROM: Predicting solution at time 2.0000e+01 using ROM.
libROM: wallclock time: 0.013560 (seconds).
libROM: Calculating diff between PDE and ROM solutions.
Writing solution file op_rom_00020.bin.
libROM: total prediction/query wallclock time: 0.285142 (seconds).
libROMInterface::saveROM() - saving ROM objects.
Saving DMD object with filename root DMD/dmdobj_0000.
Computed errors for domain 0:
L1 Error : 3.0047927793460564E-07
L2 Error : 6.4307899972723579E-07
Linfinity Error : 4.2305441628791654E-06
Conservation Errors:
2.8427194725970949E-16
2.8427194181488523E-16
9.0834458010835561E-16
2.1658175989804090E-16
Norms of the diff between ROM and PDE solutions for domain 0:
L1 Norm : 1.5215990100709741E-06
L2 Norm : 4.0657029052378237E-06
Linfinity Norm : 2.1594369212267493E-05
Solver runtime (in seconds): 1.3170622000000000E+01
Total runtime (in seconds): 1.3922789000000000E+01
Deallocating arrays.
Finished.