3D Navier-Stokes - Inviscid Shock-Cylinder Interaction (Time-Windowed DMD)
See Inviscid Shock-Cylinder Interaction to familiarize yourself with this case. This example uses a DMD object that has already been trained (see 3D Navier-Stokes - Inviscid Shock-Cylinder Interaction (Time-Windowed DMD)).
Location: hypar/Examples/3D/NavierStokes3D/2D_Shock_Cylinder_Interaction_libROM_DMD_Predict
Governing equations: 3D Navier-Stokes Equations (navierstokes3d.h - by default NavierStokes3D::Re is set to -1 which makes the code skip the parabolic terms, i.e., the 3D Euler equations are solved.)
Reduced Order Modeling: This example predicts the solution from a trained DMD object. The code does not solve the PDE by discretizing in space and integrating in time.
Domain: \(-2.5 \le x \le 7.5\), \(-5 \le y \le 5\) Note: This is a 2D flow simulated using a 3-dimensional setup by taking the length of the domain along z to be very small and with only 3 grid points (the domain size along z must be smaller than the cylinder length).
Geometry: A cylinder of radius 1.0 centered at (0,0) (hypar/Examples/STLGeometries/cylinder.stl)
Boundary conditions:
- xmin: Subsonic inflow _SUBSONIC_INFLOW_ (with post-shock flow conditions)
- xmax: Supersonic inflow _SUPERSONIC_OUTFLOW_ (with pre-shock flow conditions)
- ymin and ymax: Slip walls _SLIP_WALL_
- zmin and zmax: Periodic _PERIODIC_ (to simulate a 2D flow in the x-y plane)
- The immersed body wall is specified as adiabatic (_IB_ADIABATIC_); (this is the default).
Reference:
- O. Boiron, G. Chiavassa, R. Donat, A high-resolution penalization method for large Mach number flows in the presence of obstacles, Computers & Fluids, 38 (2009), pp. 703-714, Section 5.1
Initial solution: see reference
Other parameters:
- Specific heat ratio \(\gamma = 1.4\) (NavierStokes3D::gamma)
Reduced Order Modeling:
- Mode: predict (libROMInterface::m_mode, _ROM_MODE_PREDICT_)
- Component Mode: monolithic (libROMInterface::m_comp_mode, _ROM_COMP_MODE_MONOLITHIC_)
- Type: Dynamic Mode Decomposition (DMD) with time windowing (libROMInterface::m_rom_type)
Note:
In this mode, HyPar will run just like an usual PDE simulation, except that it will swap out the numerical spatial discretization and time integration with the ROM-based prediction. The input files and output files will be the same as a regular simulation with the following comments:
- Numerical method inputs are ignored (eg. those that specify spatial discretization and time integration methods).
- In solver.inp, the values for dt, n_iter, and file_op_iter is used only to compute the simulation times at which to compute and write the solution. The time step size, dt, need not respect any CFL criterion.
- HyPar::ConservationCheck is set to "no" since it is not possible to compute conservation loss for a general domain (because boundary fluxes are not being computed).
Input files required:
DMD Object(s) :
The trained DMD object(s) must be located in the directory specified in librom.inp as dmd_dirname (DMDROMObject::m_dirname). For this example, they were generated using 3D Navier-Stokes - Inviscid Shock-Cylinder Interaction (Time-Windowed DMD).
librom.inp
begin
mode predict
dmd_dirname DMD
end
solver.inp
begin
ndims 3
nvars 5
size 256 256 3
iproc 4 4 1
ghost 3
n_iter 10
dt 0.2
file_op_iter 1
ip_file_type binary
op_file_format binary
op_overwrite no
model navierstokes3d
immersed_body cylinder.stl
end
boundary.inp
6
subsonic-inflow 0 1 0 0 -9999.0 9999.0 -9999.0 9999.0
3.8571428571428572 2.6293687924887181 0.0 0.0
supersonic-inflow 0 -1 0 0 -9999.0 9999.0 -9999.0 9999.0
1.0 0.0 0.0 0.0 1.0
slip-wall 1 1 -9999.0 9999.0 0 0 -9999.0 9999.0
slip-wall 1 -1 -9999.0 9999.0 0 0 -9999.0 9999.0
periodic 2 1 -9999.0 9999.0 -9999.0 9999.0 0 0
periodic 2 -1 -9999.0 9999.0 -9999.0 9999.0 0 0
physics.inp
begin
gamma 1.4
upwinding roe
end
cylinder.stl : the filename "cylinder.stl" must match the input for immersed_body in solver.inp.
Located at hypar/Examples/STLGeometries/cylinder.stl
To generate initial.inp (initial solution), compile and run the following code in the run directory.
#include <stdio.h>
#include <stdlib.h>
#include <math.h>
#include <string.h>
int main()
{
const double gamma = 1.4;
int NI,NJ,NK,ndims;
char ip_file_type[50];
FILE *in;
strcpy(ip_file_type,"ascii");
printf("Reading file \"solver.inp\"...\n");
in = fopen("solver.inp","r");
if (!in) {
printf("Error: Input file \"solver.inp\" not found.\n");
return(0);
} else {
char word[500];
fscanf(in,"%s",word);
if (!strcmp(word, "begin")){
while (strcmp(word, "end")){
fscanf(in,"%s",word);
if (!strcmp(word, "ndims")) {
fscanf(in,"%d",&ndims);
} else if (!strcmp(word, "size" )) {
fscanf(in,"%d",&NI);
fscanf(in,"%d",&NJ);
fscanf(in,"%d",&NK);
} else if (!strcmp(word, "ip_file_type")) {
fscanf(in,"%s",ip_file_type);
}
}
} else {
printf("Error: Illegal format in solver.inp. Crash and burn!\n");
return(0);
}
}
fclose(in);
if (ndims != 3) {
printf("Error: ndims is not 3 in solver.inp.\n");
return(0);
}
printf("Grid: %3d x %3d x %3d.\n",NI,NJ,NK);
double Lx = 10.0; /* length of domain along x */
double Ly = 10.0; /* length of domain along y */
double xmin = -2.5; /* left x-boundary */
double ymin = -5.0; /* left y-boundary */
double xs = -2.0; /* location of initial shock */
double Ms = 3.0; /* shock Mach number */
int i,j,k;
double *x, *y, *z;
double dx, dy, dz;
x = (double*) calloc (NI, sizeof(double));
y = (double*) calloc (NJ, sizeof(double));
z = (double*) calloc (NK, sizeof(double));
dx = Lx / ((double)(NI-1));
for (i=0; i<NI; i++) x[i] = xmin + i*dx;
dy = Ly / ((double)(NJ-1));
for (j=0; j<NJ; j++) y[j] = ymin + j*dy;
dz = 0.5 * (dx +dy);
for (k = 0; k < NK; k++) z[k] = (k-NK/2) * dz;
/* pre-shock conditions */
double rho_inf = 1.0;
double p_inf = 1.0;
double u_inf = 0.0; //- Ms * sqrt(gamma*p_inf/rho_inf);
double v_inf = 0.0;
double w_inf = 0.0;
/* post-shock conditions */
double rho_ps = rho_inf * ((gamma+1.0)*Ms*Ms) / ((gamma-1.0)*Ms*Ms+2.0);
double p_ps = p_inf * (2.0*gamma*Ms*Ms-(gamma-1.0)) / (gamma+1.0);
double M2 = sqrt (((gamma-1.0)*Ms*Ms+2.0) / (2.0*gamma*Ms*Ms-(gamma-1.0)));
double u_ps = - (M2 * sqrt(gamma*p_ps/rho_ps) - Ms * sqrt(gamma*p_inf/rho_inf));
double v_ps = 0.0;
double w_ps = 0.0;
printf("Pre-shock conditions:-\n");
printf("Density = %1.16E\n", rho_inf);
printf("Pressure = %1.16E\n", p_inf );
printf("u-velocity = %1.16E\n", u_inf );
printf("v-velocity = %1.16E\n", v_inf );
printf("w-velocity = %1.16E\n", w_inf );
printf("Mach number= %1.16E\n", Ms );
printf("Post-shock conditions:-\n");
printf("Density = %1.16E\n", rho_ps);
printf("Pressure = %1.16E\n", p_ps );
printf("u-velocity = %1.16E\n", u_ps );
printf("v-velocity = %1.16E\n", v_ps );
printf("w-velocity = %1.16E\n", w_ps );
printf("Mach number= %1.16E\n", M2 );
printf("Ratios:-\n");
printf("p2/p1 = %1.16E\n",p_ps/p_inf);
printf("rho2/rho1 = %1.16E\n",rho_ps/rho_inf);
double *U = (double*) calloc (5*NI*NJ*NK, sizeof(double));
for (i = 0; i < NI; i++){
for (j = 0; j < NJ; j++){
for (k = 0; k < NK; k++){
int p = i + NI*j + NI*NJ*k;
double rho, u, v, w, P;
if (x[i] > xs) {
rho = rho_inf;
u = u_inf;
v = v_inf;
w = w_inf;
P = p_inf;
} else {
rho = rho_ps;
u = u_ps;
v = v_ps;
w = w_ps;
P = p_ps;
}
U[5*p+0] = rho;
U[5*p+1] = rho*u;
U[5*p+2] = rho*v;
U[5*p+3] = rho*w;
U[5*p+4] = P/(gamma-1.0) + 0.5*rho*(u*u+v*v+w*w);
}
}
}
FILE *out;
if (!strcmp(ip_file_type,"ascii")) {
printf("Writing ASCII initial solution file initial.inp\n");
out = fopen("initial.inp","w");
for (i = 0; i < NI; i++) fprintf(out,"%1.16E ",x[i]);
fprintf(out,"\n");
for (j = 0; j < NJ; j++) fprintf(out,"%1.16E ",y[j]);
fprintf(out,"\n");
for (k = 0; k < NK; k++) fprintf(out,"%1.16E ",z[k]);
fprintf(out,"\n");
for (k = 0; k < NK; k++) {
for (j = 0; j < NJ; j++) {
for (i = 0; i < NI; i++) {
int p = i + NK*j + NI*NJ*k;
fprintf(out,"%1.16E ",U[5*p+0]);
}
}
}
fprintf(out,"\n");
for (k = 0; k < NK; k++) {
for (j = 0; j < NJ; j++) {
for (i = 0; i < NI; i++) {
int p = i + NK*j + NI*NJ*k;
fprintf(out,"%1.16E ",U[5*p+1]);
}
}
}
fprintf(out,"\n");
for (k = 0; k < NK; k++) {
for (j = 0; j < NJ; j++) {
for (i = 0; i < NI; i++) {
int p = i + NK*j + NI*NJ*k;
fprintf(out,"%1.16E ",U[5*p+2]);
}
}
}
fprintf(out,"\n");
for (k = 0; k < NK; k++) {
for (j = 0; j < NJ; j++) {
for (i = 0; i < NI; i++) {
int p = i + NK*j + NI*NJ*k;
fprintf(out,"%1.16E ",U[5*p+3]);
}
}
}
fprintf(out,"\n");
for (k = 0; k < NK; k++) {
for (j = 0; j < NJ; j++) {
for (i = 0; i < NI; i++) {
int p = i + NK*j + NI*NJ*k;
fprintf(out,"%1.16E ",U[5*p+4]);
}
}
}
fprintf(out,"\n");
fclose(out);
} else if ((!strcmp(ip_file_type,"binary")) || (!strcmp(ip_file_type,"bin"))) {
printf("Writing binary initial solution file initial.inp\n");
out = fopen("initial.inp","wb");
fwrite(x,sizeof(double),NI,out);
fwrite(y,sizeof(double),NJ,out);
fwrite(z,sizeof(double),NK,out);
fwrite(U,sizeof(double),5*NI*NJ*NK,out);
fclose(out);
}
free(x);
free(y);
free(z);
free(U);
return(0);
}
Output:
Note that iproc is set to
4 4 1
in solver.inp (i.e., 4 processors along x, 4 processors along y, and 1 processor along z). Thus, this example should be run with 16 MPI ranks (or change iproc).
Please see the original example in the "Immersed Boundaries Examples" section for a full description of the output files and how to view them. The following only contains libROM-specific comments.
After running the code, there should be the following output files:
- 11 output file op_00000.bin, ..., op_00010.bin; these are the predicted solutions from the DMD object(s).
All the files are binary (HyPar::op_file_format is set to binary in solver.inp).
The provided Python script (plotSolution.py) can be used to generate plots from the binary files. Alternatively, HyPar::op_file_format can be set to tecplot3d, and Tecplot/VisIt or something similar can be used to plot the resulting text files.
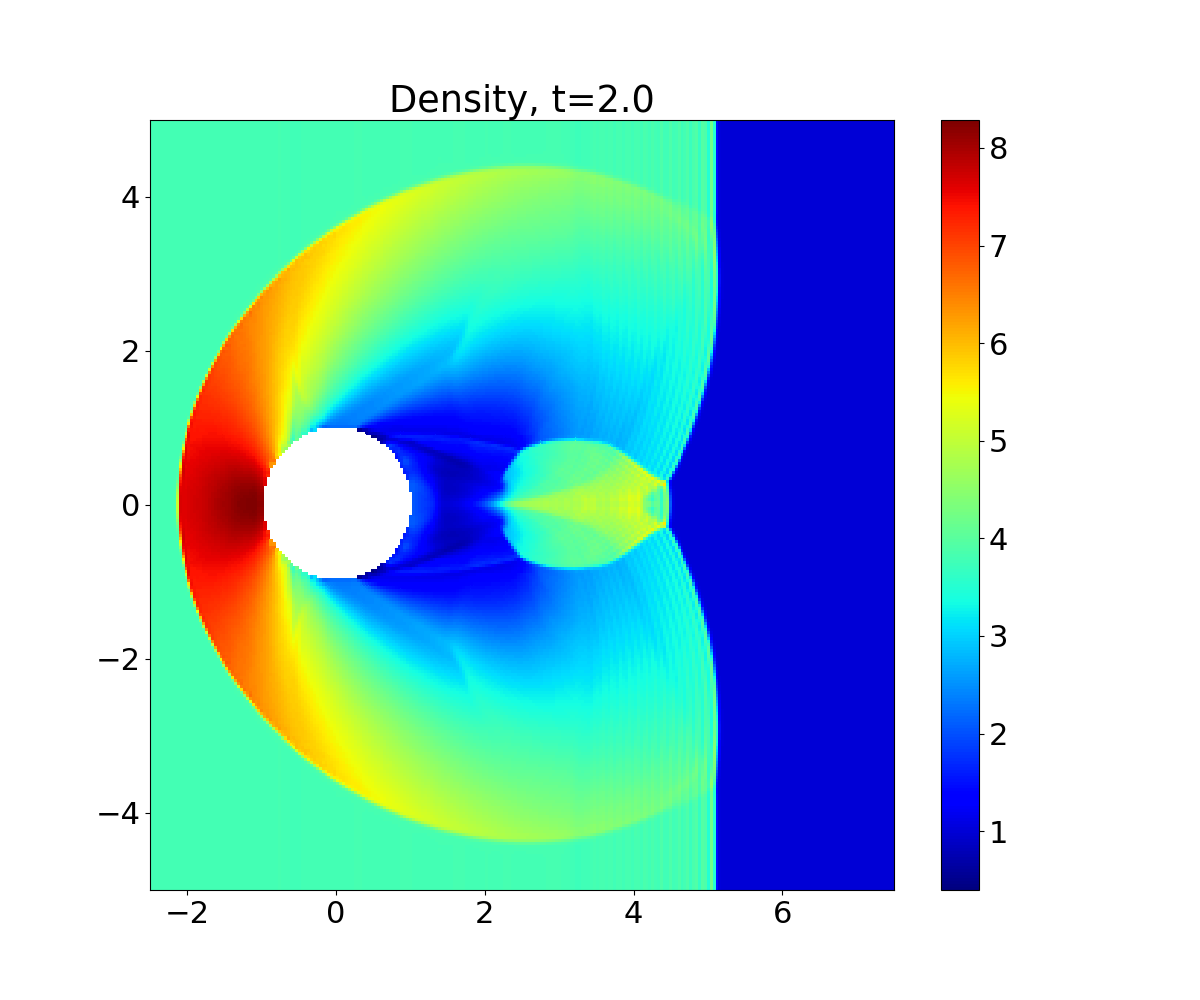
The following plot shows the density contours for the final solution (t=2).
Expected screen output:
srun: job 9716432 queued and waiting for resources
srun: job 9716432 has been allocated resources
HyPar - Parallel (MPI) version with 16 processes
Compiled with PETSc time integration.
Allocated simulation object(s).
Reading solver inputs from file "solver.inp".
No. of dimensions : 3
No. of variables : 5
Domain size : 256 256 3
Processes along each dimension : 4 4 1
Exact solution domain size : 256 256 3
No. of ghosts pts : 3
No. of iter. : 10
Restart iteration : 0
Time integration scheme : euler
Spatial discretization scheme (hyperbolic) : 1
Split hyperbolic flux term? : no
Interpolation type for hyperbolic term : characteristic
Spatial discretization type (parabolic ) : nonconservative-1stage
Spatial discretization scheme (parabolic ) : 2
Time Step : 2.000000E-01
Check for conservation : no
Screen output iterations : 1
File output iterations : 1
Initial solution file type : binary
Initial solution read mode : serial
Solution file write mode : serial
Solution file format : binary
Overwrite solution file : no
Physical model : navierstokes3d
Immersed Body : cylinder.stl
Partitioning domain and allocating data arrays.
Reading array from binary file initial.inp (Serial mode).
Volume integral of the initial solution:
0: 1.3577505742780760E+01
1: 6.1066251110367062E+00
2: 0.0000000000000000E+00
3: 0.0000000000000000E+00
4: 5.1720680582882707E+01
Reading boundary conditions from boundary.inp.
Boundary subsonic-inflow: Along dimension 0 and face +1
Boundary supersonic-inflow: Along dimension 0 and face -1
Boundary slip-wall: Along dimension 1 and face +1
Boundary slip-wall: Along dimension 1 and face -1
Boundary periodic: Along dimension 2 and face +1
Boundary periodic: Along dimension 2 and face -1
6 boundary condition(s) read.
Immersed body read from cylinder.stl:
Number of facets: 628
Bounding box: [-1.0,1.0] X [-1.0,1.0] X [-5.0,5.0]
Number of grid points inside immersed body: 6408 ( 3.3%).
Number of immersed boundary points : 1242 ( 0.6%).
Immersed body simulation mode : 2d (xy).
Initializing solvers.
Initializing physics. Model = "navierstokes3d"
Reading physical model inputs from file "physics.inp".
Writing solution file iblank_00000.bin.
Setting up libROM interface.
libROM inputs and parameters:
reduced model dimensionality: 0
sampling frequency: 0
mode: predict
type: DMD
save to file: true
libROM DMD inputs:
number of samples per window: 2147483647
directory name for DMD onjects: DMD
libROMInterface::loadROM() - loading ROM objects.
Loading DMD object (DMD/dmdobj_0000), time window=[0.00e+00,5.00e-01].
Loading DMD object (DMD/dmdobj_0001), time window=[5.00e-01,1.00e+00].
Loading DMD object (DMD/dmdobj_0002), time window=[1.00e+00,1.50e+00].
Loading DMD object (DMD/dmdobj_0003), time window=[1.50e+00,-1.00e+00].
libROM: Predicted solution at time 0.0000e+00 using ROM, wallclock time: 2.920385.
Writing immersed body surface data file surface00000.dat.
Writing solution file op_00000.bin.
libROM: Predicted solution at time 2.0000e-01 using ROM, wallclock time: 3.025760.
Writing immersed body surface data file surface00001.dat.
Writing solution file op_00001.bin.
libROM: Predicted solution at time 4.0000e-01 using ROM, wallclock time: 3.076432.
Writing immersed body surface data file surface00002.dat.
Writing solution file op_00002.bin.
libROM: Predicted solution at time 6.0000e-01 using ROM, wallclock time: 3.057626.
Writing immersed body surface data file surface00003.dat.
Writing solution file op_00003.bin.
libROM: Predicted solution at time 8.0000e-01 using ROM, wallclock time: 3.049425.
Writing immersed body surface data file surface00004.dat.
Writing solution file op_00004.bin.
libROM: Predicted solution at time 1.0000e+00 using ROM, wallclock time: 3.158879.
Writing immersed body surface data file surface00005.dat.
Writing solution file op_00005.bin.
libROM: Predicted solution at time 1.2000e+00 using ROM, wallclock time: 3.187523.
Writing immersed body surface data file surface00006.dat.
Writing solution file op_00006.bin.
libROM: Predicted solution at time 1.4000e+00 using ROM, wallclock time: 3.042254.
Writing immersed body surface data file surface00007.dat.
Writing solution file op_00007.bin.
libROM: Predicted solution at time 1.6000e+00 using ROM, wallclock time: 3.046216.
Writing immersed body surface data file surface00008.dat.
Writing solution file op_00008.bin.
libROM: Predicted solution at time 1.8000e+00 using ROM, wallclock time: 3.068598.
Writing immersed body surface data file surface00009.dat.
Writing solution file op_00009.bin.
libROM: Predicted solution at time 2.0000e+00 using ROM, wallclock time: 3.130178.
Writing immersed body surface data file surface00010.dat.
Writing solution file op_00010.bin.
libROM: total prediction/query wallclock time: 33.763276 (seconds).
Solver runtime (in seconds): 9.7125058999999993E+01
Total runtime (in seconds): 9.7660359999999997E+01
Deallocating arrays.
Finished.