HyPar  1.0
Finite-Difference Hyperbolic-Parabolic PDE Solver on Cartesian Grids
3D Navier-Stokes Equations - Rising Thermal Bubble

See 3D Navier-Stokes Equations - Rising Thermal Bubble to familiarize yourself with this case.

Location: hypar/Examples/3D/NavierStokes3D/RisingThermalBubble_Config1_CUDA (This directory contains all the input files needed to run this case.)

Governing equations: 3D Navier-Stokes Equations (navierstokes3d.h)

Domain: \(0 \le x,y,z < 1000\,{\rm m}\), "slip-wall" (_SLIP_WALL_) boundaries everywhere, with zero wall velocity.

Reference:

  • Kelly, J. F., Giraldo, F. X., "Continuous and discontinuous Galerkin methods for a scalable three-dimensional nonhydrostatic atmospheric model: Limited-area mode", J. Comput. Phys., 231, 2012, pp. 7988-8008 (see section 5.1.2).
  • Giraldo, F. X., Kelly, J. F., Constantinescu, E. M., "Implicit-Explicit Formulations of a Three-Dimensional Nonhydrostatic Unified Model of the Atmosphere (NUMA)", SIAM J. Sci. Comput., 35 (5), 2013, pp. B1162-B1194 (see section 4.1).

Initial solution: A warm bubble in cool ambient atmosphere. Note that in this example, the gravitational forces and rising of the bubble is along the y-axis.

Other parameters (all dimensional quantities are in SI units):

Numerical Method:

Hardware Details:

  • GPU: NVIDIA V100 (Volta)
  • CPU: IBM Power9
  • Configuration: 1 node, 1 GPU and 1 MPI rank

Input files required:

solver.inp

begin
ndims 3
nvars 5
size 64 64 64
iproc 1 1 1
ghost 3
n_iter 8000
restart_iter 0
time_scheme rk
time_scheme_type 44
hyp_space_scheme weno5
hyp_flux_split no
hyp_interp_type components
dt 0.025
conservation_check no
screen_op_iter 100
file_op_iter 500
input_mode parallel 1
ip_file_type binary
output_mode serial
op_file_format binary
op_overwrite no
model navierstokes3d
use_gpu yes
gpu_device_no -1
end

boundary.inp

6
slip-wall 0 1 0 0 0 1000.0 0 1000.0
0.0 0.0 0.0
slip-wall 0 -1 0 0 0 1000.0 0 1000.0
0.0 0.0 0.0
slip-wall 1 1 0 1000.0 0 0 0 1000.0
0.0 0.0 0.0
slip-wall 1 -1 0 1000.0 0 0 0 1000.0
0.0 0.0 0.0
slip-wall 2 1 0 1000.0 0 1000.0 0 0
0.0 0.0 0.0
slip-wall 2 -1 0 1000.0 0 1000.0 0 0
0.0 0.0 0.0

physics.inp

begin
gamma 1.4
upwinding rusanov
gravity 0.0 9.8 0.0
rho_ref 1.1612055171196529
p_ref 100000.0
R 287.058
HB 2
end

weno.inp (optional)

begin
mapped 0
borges 0
yc 1
no_limiting 0
epsilon 0.000001
p 2.0
rc 0.3
xi 0.001
end

To generate initial_par.inp.* (initial solution), compile and run the following code in the run directory.

/*
This code generates the initial solution for the rising
thermal bubble case for the 3D Navier-Stokes equations.
The initial solution is written for the local (MPI) sub-domains,
and the number of files written depend on the number of I/O ranks.
Although this code is serial, it will compute the decomposition
of the global domain and generate the initial solution accordingly.
+ "input_mode" in solver.inp must be set to "parallel n" where n
is the number of I/O ranks.
+ "ip_file_type" in solver.inp must be set to "binary".
Note: this code does *not* involve the allocation of the global domain,
thus its memory use depends only on the size of the local domain.
*/
#define _MAX_STRING_SIZE_ 50
#include <stdlib.h>
#include <stdio.h>
#include <string.h>
#include <math.h>
#define _ArrayIncrementIndex_(N,imax,i,done) \
{ \
int arraycounter = 0; \
while (arraycounter < (N)) { \
if (i[arraycounter] == imax[arraycounter]-1) { \
i[arraycounter] = 0; \
arraycounter++; \
} else { \
i[arraycounter]++; \
break; \
} \
} \
if (arraycounter == (N)) done = 1; \
else done = 0; \
}
#define _ArrayIndex1D_(N,imax,i,ghost,index) \
{ \
index = i[N-1]+(ghost); \
int arraycounter; \
for (arraycounter = (N)-2; arraycounter > -1; arraycounter--) { \
index = ((index*(imax[arraycounter]+2*(ghost))) + (i[arraycounter]+(ghost))); \
} \
}
double raiseto(double x, double a)
{
return(exp(a*log(x)));
}
void GetStringFromInteger(int a,char *A,int width)
{
int i;
for (i=0; i<width; i++) {
char digit = (char) (a%10 + '0');
a /= 10;
A[width-1-i] = digit;
}
return;
}
void MPIGetFilename(char *root,int rank,char *filename)
{
char tail[_MAX_STRING_SIZE_] = "";
GetStringFromInteger(rank,tail,4);
strcpy(filename,"");
strcat(filename,root);
strcat(filename,"." );
strcat(filename,tail);
return;
}
int MPIRanknD(int ndims,int rank,int* iproc,int *ip)
{
int i,term = 1;
for (i=0; i<ndims; i++) term *= iproc[i];
for (i=ndims-1; i>=0; i--) {
term /= iproc[i];
ip[i] = rank/term;
rank -= ip[i]*term;
}
return(0);
}
int MPIPartition1D(int nglobal,int nproc,int rank)
{
int nlocal;
if (nglobal%nproc == 0) nlocal = nglobal/nproc;
else {
if (rank == nproc-1) nlocal = nglobal/nproc + nglobal%nproc;
else nlocal = nglobal/nproc;
}
return(nlocal);
}
int MPILocalDomainLimits(int ndims,int p,int *iproc,int *dim_global,int *is, int *ie)
{
int i;
int ip[ndims];
MPIRanknD(ndims,p,iproc,ip);
for (i=0; i<ndims; i++) {
int imax_local, isize, root = 0;
imax_local = MPIPartition1D(dim_global[i],iproc[i],root );
isize = MPIPartition1D(dim_global[i],iproc[i],ip[i]);
if (is) is[i] = ip[i]*imax_local;
if (ie) ie[i] = ip[i]*imax_local + isize;
}
return(0);
}
int main()
{
FILE *in, *out;
int NI, NJ, NK, ndims, nvars, size, bytes, N_IORanks, i, j, k;
int *dim_global,*dim_local,*iproc;
char ip_file_type[_MAX_STRING_SIZE_], input_mode[_MAX_STRING_SIZE_], fnameout[_MAX_STRING_SIZE_];
strcpy (ip_file_type,"ascii");
strcpy (fnameout,"initial_par.inp");
printf("Reading file \"solver.inp\"...\n");
in = fopen("solver.inp","r");
if (!in) {
fprintf(stderr,"Error: File \"solver.inp\" not found.\n");
return(0);
} else {
char word[_MAX_STRING_SIZE_];
fscanf(in,"%s",word);
if (!strcmp(word, "begin")){
while (strcmp(word, "end")){
fscanf(in,"%s",word);
if (!strcmp(word, "ndims")) {
fscanf(in,"%d",&ndims);
dim_global = (int*) calloc (ndims,sizeof(int));
dim_local = (int*) calloc (ndims,sizeof(int));
iproc = (int*) calloc (ndims,sizeof(int));
} else if (!strcmp(word, "nvars")) {
fscanf(in,"%d",&nvars);
} else if (!strcmp(word, "size")) {
int i;
if (!dim_global) {
fprintf(stderr,"Error in ReadInputs(): dim_global not allocated.\n");
fprintf(stderr,"Please specify ndims before dimensions.\n" );
return 0;
} else {
for (i=0; i<ndims; i++) fscanf(in,"%d",&dim_global[i]);
}
} else if (!strcmp(word, "iproc")) {
int i;
if (!iproc) {
fprintf(stderr,"Error in ReadInputs(): iproc not allocated.\n");
fprintf(stderr,"Please specify ndims before iproc.\n" );
return 0;
} else {
for (i=0; i<ndims; i++) fscanf(in,"%d",&iproc[i]);
}
} else if (!strcmp(word, "ip_file_type" )) {
fscanf(in,"%s",ip_file_type);
} else if (!strcmp(word, "input_mode")) {
fscanf(in,"%s",input_mode);
if (strcmp(input_mode,"serial")) fscanf(in,"%d",&N_IORanks);
}
}
} else {
fprintf(stderr,"Error: Illegal format in file \"solver.inp\".\n");
return 0;
}
fclose(in);
/* Print to screen the inputs read */
printf("\tNo. of dimensions : %d\n",ndims);
printf("\tNo. of variables : %d\n",nvars);
printf("\tDomain size : ");
for (i=0; i<ndims; i++) printf ("%d ",dim_global[i]);
printf("\n");
printf("\tProcesses along each dimension : ");
for (i=0; i<ndims; i++) printf ("%d ",iproc[i]);
printf("\n");
printf("\tInitial solution file type : %s\n",ip_file_type);
printf("\tInitial solution read mode : %s\n",input_mode );
printf("\tNumber of IO ranks : %d\n",N_IORanks );
}
if (ndims != 3) {
printf("ndims is not 3 in solver.inp. this code is to generate 3D exact solution\n");
return(0);
}
if (!strcmp(ip_file_type,"ascii")) {
printf("Error: ip_file_type *must* be specified and set to \"binary\" in solver.inp.\n");
return(0);
}
if (strcmp(input_mode,"parallel")) {
printf("Error: input_mode is not \"parallel\".\n");
return 0;
}
/* read in physics stuff */
double gamma = 1.4;
double R = 287.058;
double rho_ref = 1.1612055171196529;
double p_ref = 100000.0;
double grav_x = 0.0;
double grav_y = 9.8;
double grav_z = 0.0;
int HB = 0;
printf("Reading file \"physics.inp\"...\n");
in = fopen("physics.inp","r");
if (!in) {
printf("Error: Input file \"physics.inp\" not found.\n");
return(0);
} else {
char word[500];
fscanf(in,"%s",word);
if (!strcmp(word, "begin")) {
while (strcmp(word, "end")) {
fscanf(in,"%s",word);
if (!strcmp(word, "rho_ref")) fscanf(in,"%lf",&rho_ref);
else if (!strcmp(word, "p_ref" )) fscanf(in,"%lf",&p_ref );
else if (!strcmp(word, "gamma" )) fscanf(in,"%lf",&gamma );
else if (!strcmp(word, "R" )) fscanf(in,"%lf",&R );
else if (!strcmp(word, "HB" )) fscanf(in,"%d" ,&HB );
else if (!strcmp(word, "gravity")) {
fscanf(in,"%lf",&grav_x );
fscanf(in,"%lf",&grav_y );
fscanf(in,"%lf",&grav_z );
}
}
} else printf("Error: Illegal format in physics.inp. Crash and burn!\n");
}
fclose(in);
if (HB != 2) {
printf("Error: Specify \"HB\" as 2 in physics.inp.\n");
}
if ((grav_x != 0.0) || (grav_z != 0.0)) {
printf("Error: gravity must be zero along x and z for this example.\n");
return(0);
}
/* Define the domain */
double xmin, xmax, ymin, ymax, zmin, zmax;
xmin = 0.0;
xmax = 1000.0;
ymin = 0.0;
ymax = 1000.0;
zmin = 0.0;
zmax = 1000.0 ;
NI = dim_global[0];
NJ = dim_global[1];
NK = dim_global[2];
double Lx = xmax - xmin;
double Ly = ymax - ymin;
double Lz = zmax - zmin;
double dx = Lx / ((double)NI-1);
double dy = Ly / ((double)NJ-1);
double dz = Lz / ((double)NK-1);
/* Initial perturbation center */
double xc = 500;
double yc = 260;
double zc = 500;
/* initial perturbation parameters */
double pi = 4.0*atan(1.0);
double rc = 250.0;
double Cp = gamma * R / (gamma-1.0);
double T_ref = p_ref / (R * rho_ref);
printf("Generating grid.\n");
double *Xg = (double*) calloc (NI+NJ+NK, sizeof(double));
double *x = Xg, *y = Xg+NI, *z = Xg+NI+NJ;
for (i = 0; i < NI; i++){
for (j = 0; j < NJ; j++){
for (k = 0; k < NK; k++){
x[i] = xmin + i*dx;
y[j] = ymin + j*dy;
z[k] = zmin + k*dz;
}
}
}
int nproc = 1;
for (i=0; i<ndims; i++) nproc *= iproc[i];
if (nproc%N_IORanks != 0) N_IORanks = 1;
printf("Splitting data into %d processes. Will generate %d files (one for each file IO rank).\n",
nproc,N_IORanks);
int proc,IORank;
int GroupSize = nproc / N_IORanks;
for (IORank = 0; IORank < N_IORanks; IORank++) {
printf("Generating and writing local solutions for IORank %d.\n",IORank);
char out_filename[_MAX_STRING_SIZE_];
MPIGetFilename(fnameout,IORank,out_filename);
int Start = IORank * GroupSize;
int End = (IORank+1) * GroupSize;
out = fopen(out_filename,"wb");
for (proc=Start; proc < End; proc++) {
int ip[ndims],is[ndims],ie[ndims];
double *Xl, *Ul;
MPIRanknD(ndims,proc,iproc,ip);
MPILocalDomainLimits(ndims,proc,iproc,dim_global,is,ie);
for (i=0; i<ndims; i++) dim_local[i] = ie[i]-is[i];
size = 0; for (i=0; i<ndims; i++) size += dim_local[i];
Xl = (double*) calloc (size, sizeof(double));
int offsetl=0, offsetg=0;
for (i=0; i<ndims; i++) {
int p; for (p=0; p<dim_local[i]; p++) Xl[p+offsetl] = Xg[p+is[i]+offsetg];
offsetl += dim_local[i];
offsetg += dim_global[i];
}
x = Xl;
y = Xl + dim_local[0];
z = Xl + dim_local[0] + dim_local[1];
size = nvars; for (i=0; i<ndims; i++) size *= dim_local[i];
Ul = (double*) calloc (size, sizeof(double));
int done = 0; int index[ndims]; for(i=0; i<ndims; i++) index[i]=0;
while (!done) {
int p; _ArrayIndex1D_(ndims,dim_local ,index,0,p);
i = index[0]; j = index[1]; k = index[2];
double r = sqrt((x[i]-xc)*(x[i]-xc)+(y[j]-yc)*(y[j]-yc)+(z[k]-zc)*(z[k]-zc));
double dtheta = (r>rc ? 0.0 : (0.5*(1.0+cos(pi*r/rc))) );
double theta = T_ref + dtheta;
double Pexner = 1.0 - (grav_y*y[j])/(Cp*T_ref);
double rho = (p_ref/(R*theta)) * raiseto(Pexner, (1.0/(gamma-1.0)));
double E = rho * (R/(gamma-1.0)) * theta*Pexner;
Ul[5*p+0] = rho;
Ul[5*p+1] = 0.0;
Ul[5*p+2] = 0.0;
Ul[5*p+3] = 0.0;
Ul[5*p+4] = E;
_ArrayIncrementIndex_(ndims,dim_local,index,done);
}
size = 0; for (i=0; i<ndims; i++) size += dim_local[i];
bytes = fwrite(Xl,sizeof(double),size,out);
if (bytes != size) printf("Error: Unable to write grid data to file %s.\n",fnameout);
size = nvars; for (i=0; i<ndims; i++) size *= dim_local[i];
bytes = fwrite(Ul,sizeof(double),size,out);
if (bytes != size) printf("Error: Unable to write solution data to file %s.\n",fnameout);
free(Xl);
free(Ul);
}
fclose(out);
}
free(dim_global);
free(dim_local);
free(iproc);
free(Xg);
return(0);
}

Output:

Note that iproc is set to 

  1 1 1

in solver.inp This example should be run with 1 MPI rank and 1 GPU.

After running the code, there should be 17 output files op_00000.bin, op_00001.bin, ... op_00016.bin; the first one is the solution at \(t=0\) and the final one is the solution at \(t=200\,{\rm s}\).

See 3D Navier-Stokes Equations - Rising Thermal Bubble for detailed postprocessing instructions.
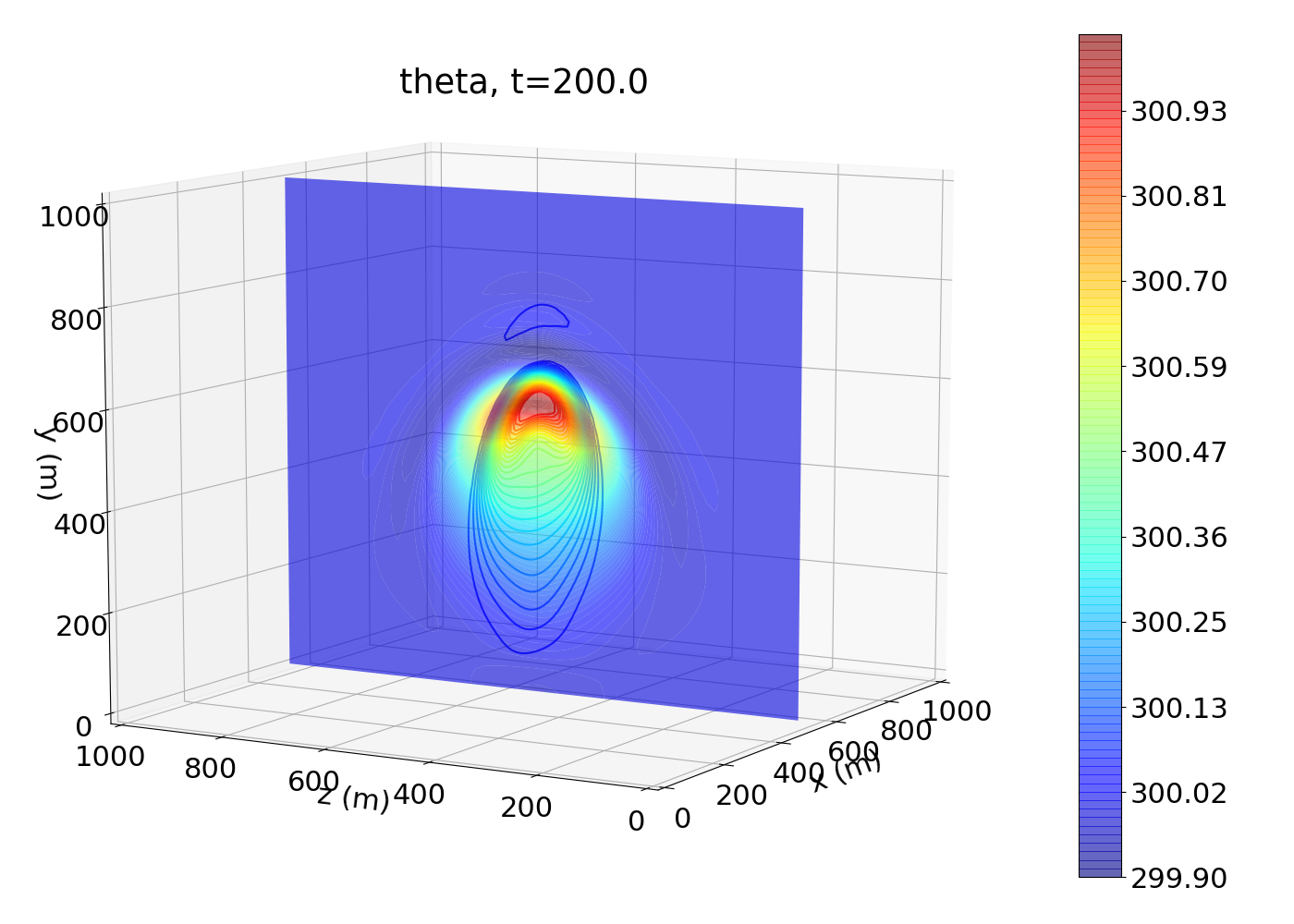
The following figure is generated using aux/plotSolution.py and shows the potential temperature at the final time. Colored contours are plotted in the X-Y plane, and contour lines are plotted in the Z-Y plane:

Solution_3DNavStok_Bubble3D_CUDA.png

Expected screen output:

HyPar - Parallel (MPI) version with 1 processes
Allocated simulation object(s).
Reading solver inputs from file "solver.inp".
No. of dimensions : 3
No. of variables : 5
Domain size : 64 64 64
Processes along each dimension : 1 1 1
Exact solution domain size : 64 64 64
No. of ghosts pts : 3
No. of iter. : 8000
Restart iteration : 0
Time integration scheme : rk (44)
Spatial discretization scheme (hyperbolic) : weno5
Split hyperbolic flux term? : no
Interpolation type for hyperbolic term : components
Spatial discretization type (parabolic ) : nonconservative-1stage
Spatial discretization scheme (parabolic ) : 2
Time Step : 2.500000E-02
Check for conservation : no
Screen output iterations : 100
File output iterations : 500
Initial solution file type : binary
Initial solution read mode : parallel [1 file IO rank(s)]
Solution file write mode : serial
Solution file format : binary
Overwrite solution file : no
Use GPU : yes
GPU device no : -1
Physical model : navierstokes3d
Partitioning domain and allocating data arrays.
Reading from binary file initial_par.inp.xxx (parallel mode).
Volume integral of the initial solution:
0: 1.1686650873137891E+09
1: 0.0000000000000000E+00
2: 0.0000000000000000E+00
3: 0.0000000000000000E+00
4: 2.4758406164999706E+14
Reading boundary conditions from boundary.inp.
Boundary slip-wall: Along dimension 0 and face +1
Boundary slip-wall: Along dimension 0 and face -1
Boundary slip-wall: Along dimension 1 and face +1
Boundary slip-wall: Along dimension 1 and face -1
Boundary slip-wall: Along dimension 2 and face +1
Boundary slip-wall: Along dimension 2 and face -1
6 boundary condition(s) read.
Initializing solvers.
Reading WENO parameters from weno.inp.
Initializing physics. Model = "navierstokes3d"
Reading physical model inputs from file "physics.inp".
Setting up time integration.
Solving in time (from 0 to 8000 iterations)
Writing solution file op_00000.bin.
iter= 100 t=2.500E+00 wctime: 2.1E-02 (s)
iter= 200 t=5.000E+00 wctime: 2.1E-02 (s)
iter= 300 t=7.500E+00 wctime: 2.1E-02 (s)
iter= 400 t=1.000E+01 wctime: 2.1E-02 (s)
iter= 500 t=1.250E+01 wctime: 2.1E-02 (s)
Writing solution file op_00001.bin.
iter= 600 t=1.500E+01 wctime: 2.1E-02 (s)
iter= 700 t=1.750E+01 wctime: 2.1E-02 (s)
iter= 800 t=2.000E+01 wctime: 2.1E-02 (s)
iter= 900 t=2.250E+01 wctime: 2.1E-02 (s)
iter= 1000 t=2.500E+01 wctime: 2.1E-02 (s)
Writing solution file op_00002.bin.
iter= 1100 t=2.750E+01 wctime: 2.1E-02 (s)
iter= 1200 t=3.000E+01 wctime: 2.1E-02 (s)
iter= 1300 t=3.250E+01 wctime: 2.1E-02 (s)
iter= 1400 t=3.500E+01 wctime: 2.1E-02 (s)
iter= 1500 t=3.750E+01 wctime: 2.1E-02 (s)
Writing solution file op_00003.bin.
iter= 1600 t=4.000E+01 wctime: 2.1E-02 (s)
iter= 1700 t=4.250E+01 wctime: 2.1E-02 (s)
iter= 1800 t=4.500E+01 wctime: 2.1E-02 (s)
iter= 1900 t=4.750E+01 wctime: 2.1E-02 (s)
iter= 2000 t=5.000E+01 wctime: 2.1E-02 (s)
Writing solution file op_00004.bin.
iter= 2100 t=5.250E+01 wctime: 2.1E-02 (s)
iter= 2200 t=5.500E+01 wctime: 2.1E-02 (s)
iter= 2300 t=5.750E+01 wctime: 2.1E-02 (s)
iter= 2400 t=6.000E+01 wctime: 2.1E-02 (s)
iter= 2500 t=6.250E+01 wctime: 2.1E-02 (s)
Writing solution file op_00005.bin.
iter= 2600 t=6.500E+01 wctime: 2.1E-02 (s)
iter= 2700 t=6.750E+01 wctime: 2.1E-02 (s)
iter= 2800 t=7.000E+01 wctime: 2.1E-02 (s)
iter= 2900 t=7.250E+01 wctime: 2.1E-02 (s)
iter= 3000 t=7.500E+01 wctime: 2.1E-02 (s)
Writing solution file op_00006.bin.
iter= 3100 t=7.750E+01 wctime: 2.1E-02 (s)
iter= 3200 t=8.000E+01 wctime: 2.1E-02 (s)
iter= 3300 t=8.250E+01 wctime: 2.1E-02 (s)
iter= 3400 t=8.500E+01 wctime: 2.1E-02 (s)
iter= 3500 t=8.750E+01 wctime: 2.1E-02 (s)
Writing solution file op_00007.bin.
iter= 3600 t=9.000E+01 wctime: 2.1E-02 (s)
iter= 3700 t=9.250E+01 wctime: 2.1E-02 (s)
iter= 3800 t=9.500E+01 wctime: 2.1E-02 (s)
iter= 3900 t=9.750E+01 wctime: 2.1E-02 (s)
iter= 4000 t=1.000E+02 wctime: 2.1E-02 (s)
Writing solution file op_00008.bin.
iter= 4100 t=1.025E+02 wctime: 2.1E-02 (s)
iter= 4200 t=1.050E+02 wctime: 2.1E-02 (s)
iter= 4300 t=1.075E+02 wctime: 2.1E-02 (s)
iter= 4400 t=1.100E+02 wctime: 2.1E-02 (s)
iter= 4500 t=1.125E+02 wctime: 2.1E-02 (s)
Writing solution file op_00009.bin.
iter= 4600 t=1.150E+02 wctime: 2.1E-02 (s)
iter= 4700 t=1.175E+02 wctime: 2.1E-02 (s)
iter= 4800 t=1.200E+02 wctime: 2.1E-02 (s)
iter= 4900 t=1.225E+02 wctime: 2.1E-02 (s)
iter= 5000 t=1.250E+02 wctime: 2.1E-02 (s)
Writing solution file op_00010.bin.
iter= 5100 t=1.275E+02 wctime: 2.1E-02 (s)
iter= 5200 t=1.300E+02 wctime: 2.1E-02 (s)
iter= 5300 t=1.325E+02 wctime: 2.1E-02 (s)
iter= 5400 t=1.350E+02 wctime: 2.1E-02 (s)
iter= 5500 t=1.375E+02 wctime: 2.1E-02 (s)
Writing solution file op_00011.bin.
iter= 5600 t=1.400E+02 wctime: 2.1E-02 (s)
iter= 5700 t=1.425E+02 wctime: 2.1E-02 (s)
iter= 5800 t=1.450E+02 wctime: 2.1E-02 (s)
iter= 5900 t=1.475E+02 wctime: 2.1E-02 (s)
iter= 6000 t=1.500E+02 wctime: 2.1E-02 (s)
Writing solution file op_00012.bin.
iter= 6100 t=1.525E+02 wctime: 2.1E-02 (s)
iter= 6200 t=1.550E+02 wctime: 2.1E-02 (s)
iter= 6300 t=1.575E+02 wctime: 2.1E-02 (s)
iter= 6400 t=1.600E+02 wctime: 2.1E-02 (s)
iter= 6500 t=1.625E+02 wctime: 2.1E-02 (s)
Writing solution file op_00013.bin.
iter= 6600 t=1.650E+02 wctime: 2.1E-02 (s)
iter= 6700 t=1.675E+02 wctime: 2.1E-02 (s)
iter= 6800 t=1.700E+02 wctime: 2.1E-02 (s)
iter= 6900 t=1.725E+02 wctime: 2.1E-02 (s)
iter= 7000 t=1.750E+02 wctime: 2.1E-02 (s)
Writing solution file op_00014.bin.
iter= 7100 t=1.775E+02 wctime: 2.1E-02 (s)
iter= 7200 t=1.800E+02 wctime: 2.1E-02 (s)
iter= 7300 t=1.825E+02 wctime: 2.1E-02 (s)
iter= 7400 t=1.850E+02 wctime: 2.1E-02 (s)
iter= 7500 t=1.875E+02 wctime: 2.1E-02 (s)
Writing solution file op_00015.bin.
iter= 7600 t=1.900E+02 wctime: 2.1E-02 (s)
iter= 7700 t=1.925E+02 wctime: 2.1E-02 (s)
iter= 7800 t=1.950E+02 wctime: 2.1E-02 (s)
iter= 7900 t=1.975E+02 wctime: 2.1E-02 (s)
iter= 8000 t=2.000E+02 wctime: 2.1E-02 (s)
Completed time integration (Final time: 200.000000), total wctime: 169.173154 (seconds).
Writing solution file op_00016.bin.
Solver runtime (in seconds): 1.6979008400000001E+02
Total runtime (in seconds): 1.7032046900000000E+02
Deallocating arrays.
Finished.