C++ declarations for MPI-related functions. More...

#include <mpivars_struct.h>

Functions
int	MPIBroadcast_double (double , int, int, void )

int	MPIBroadcast_integer (int , int, int, void )

int	MPIBroadcast_character (char , int, int, void )

int	MPICreateCommunicators (int, void *)

int	MPIFreeCommunicators (int, void *)

int	MPICreateIOGroups (void *)

int	MPIExchangeBoundaries1D (void , double , int, int, int, int)

int	MPIExchangeBoundariesnD (int, int, int , int, void , double *)

int	MPIGatherArray1D (void , double , double *, int, int, int, int)

int	MPIGatherArraynD (int, void , double , double , int , int *, int, int)

int	MPIGatherArraynDwGhosts (int, void , double , double , int , int *, int, int)

int	MPIPartitionArraynD (int, void , double , double , int , int *, int, int)

int	MPIPartitionArraynDwGhosts (int, void , double , double , int , int *, int, int)

int	MPIPartitionArray1D (void , double , double *, int, int, int, int)

int	MPIGetArrayDatanD (double , double , int , int , int , int , int, int, int, void *)

int	MPILocalDomainLimits (int, int, void , int , int , int )

int	MPIMax_integer (int , int , int, void *)

int	MPIMax_long (long , long , int, void *)

int	MPIMax_double (double , double , int, void *)

int	MPIMin_integer (int , int , int, void *)

int	MPIMin_double (double , double , int, void *)

int	MPISum_double (double , double , int, void *)

int	MPISum_integer (int , int , int, void *)

int	MPIPartition1D (int, int, int)

int	MPIRank1D (int, int , int )

int	MPIRanknD (int, int, int , int )

void	MPIGetFilename (char , void , char *)

Detailed Description

C++ declarations for MPI-related functions.

Author: Debojyoti Ghosh

Definition in file mpivars_cpp.h.

Function Documentation

int MPIBroadcast_double	(	double *	x,
		int	size,
		int	root,
		void *	comm
	)

Broadcast a double to all ranks

Broadcast an array of type double to all MPI ranks

Parameters

x	array to broadcast to all ranks
size	size of array to broadcast
root	rank from which to broadcast
comm	MPI communicator within which to broadcast

Definition at line 9 of file MPIBroadcast.c.

 {
 #ifndef serial
   MPI_Bcast(x,size,MPI_DOUBLE,root,*((MPI_Comm*)comm));
 #endif
   return(0);
 }

int MPIBroadcast_integer	(	int *	x,
		int	size,
		int	root,
		void *	comm
	)

Broadcast an integer to all ranks

Broadcast an array of type int to all MPI ranks

Parameters

x	array to broadcast to all ranks
size	size of array to broadcast
root	rank from which to broadcast
comm	MPI communicator within which to broadcast

Definition at line 23 of file MPIBroadcast.c.

 {
 #ifndef serial
   MPI_Bcast(x,size,MPI_INT,root,*((MPI_Comm*)comm));
 #endif
   return(0);
 }

int MPIBroadcast_character	(	char *	x,
		int	size,
		int	root,
		void *	comm
	)

Broadcast a character to all ranks

Broadcast an array of type char to all MPI ranks

Parameters

x	array to broadcast to all ranks
size	size of array to broadcast
root	rank from which to broadcast
comm	MPI communicator within which to broadcast

Definition at line 37 of file MPIBroadcast.c.

 {
 #ifndef serial
   MPI_Bcast(x,size,MPI_CHAR,root,*((MPI_Comm*)comm));
 #endif
   return(0);
 }

int MPICreateCommunicators	(	int	ndims,
		void *	m
	)

Create communicators required for the tridiagonal solver in compact schemes

Create subcommunicators from MPI_WORLD, where each subcommunicator contains MPI ranks along a spatial dimension. Consider a two-dimensional problem, partitioned on 21 MPI ranks as follows:

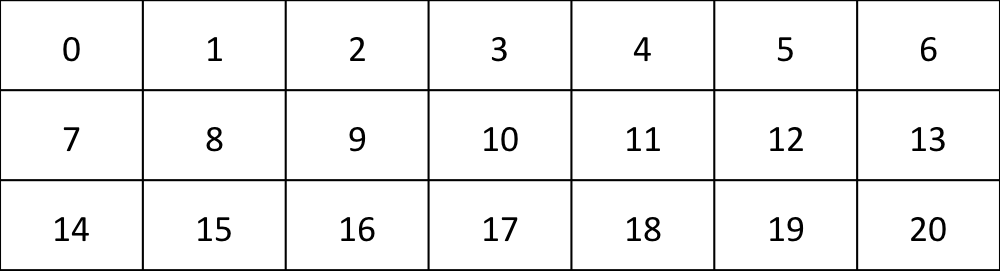
This function will create 10 subcommunicators with the following ranks:

0,1,2,3,4,5,6
7,8,9,10,11,12,13
14,15,16,17,18,19,20
0,7,14
1,8,15
2,9,16
3,10,17
4,11,18
5,12,19
6,13,20

These subcommunicators are useful for parallel computations along grid lines. For example, a compact finite-difference scheme solves implicit systems along grid lines in every spatial dimension. Thus, the subcommunicator may be passed on to the parallel systems solver instead of MPI_WORLD.

Parameters

ndims	Number of spatial dimensions
m	MPI object of type MPIVariables

Definition at line 35 of file MPICommunicators.c.

 {
   MPIVariables *mpi = (MPIVariables*) m;
 #ifdef serial
   mpi->comm = NULL;
 #else
   int          i,n,color,key;
   int          *ip,*iproc;
 
   mpi->comm = (MPI_Comm*) calloc (ndims, sizeof(MPI_Comm));
   if (ndims == 1) MPI_Comm_dup(mpi->world,mpi->comm);
   else {
     ip    = (int*) calloc (ndims-1,sizeof(int));
     iproc = (int*) calloc (ndims-1,sizeof(int));
     for (n=0; n<ndims; n++) {
       int tick=0; 
       for (i=0; i<ndims; i++) {
         if (i != n) {
           ip[tick]    = mpi->ip[i];
           iproc[tick] = mpi->iproc[i];
           tick++;
         }
       }
       _ArrayIndex1D_(ndims-1,iproc,ip,0,color); 
       key   = mpi->ip[n];
       MPI_Comm_split(mpi->world,color,key,&mpi->comm[n]);
     }
     free(ip);
     free(iproc);
   }
 #endif
   return(0);
 }

int MPIFreeCommunicators	(	int	ndims,
		void *	m
	)

Free/destroy communicators created

Free the subcommunicators created in MPICreateCommunicators().

Parameters

ndims	Number of spatial dimensions
m	MPI object of type MPIVariables

Definition at line 75 of file MPICommunicators.c.

 {
 #ifndef serial
   MPIVariables *mpi = (MPIVariables*) m;
   int          n;
   for (n=0; n<ndims; n++) MPI_Comm_free(&mpi->comm[n]);
   free(mpi->comm);
   if (mpi->IOParticipant) MPI_Comm_free(&mpi->IOWorld);
   MPI_Comm_free(&mpi->world);
 #endif
   return(0);
 }

int MPICreateIOGroups ( void * m )

Create I/O groups for file reading and writing – Group leaders gather data from all other ranks in the group and write to file, and read from file and sends the data to the appropriate ranks in the group. Thus, number of ranks participating in file I/O is equal to the number of groups (which is an input), and can be set to the number of I/O nodes available.

Create I/O groups of MPI ranks: A scalable approach to file I/O when running simulations on a large number of processors (>10,000) is partitioning all the MPI ranks into I/O group. Each group has a "leader" that:

Input - reads the local data of each member rank from the file and sends it to that member.
Output - gets the local data of each member rank and writes it to a file.

The number of I/O groups (and hence, the number of I/O ranks reading and writing to files) is specified through MPIVariables::N_IORanks. Ideally, this would correspond to the number of I/O nodes available for the total number of compute nodes being used on a HPC platform.

Two extreme cases are:

Number of I/O ranks is 1, i.e., just one rank (typically rank 0) is responsible for reading and writing the local data of every rank.
Number of I/O ranks is equal to the total number of MPI ranks, i.e., each MPI rank reads and writes from and to its own files.

Neither of the extreme cases are scalable.

Notes:

If the total number of MPI ranks (MPIVariables::nproc) is not an integer multiple of the specified number of I/O groups (MPIVariables::N_IORanks), then only 1 rank is used.

Parameters

m	MPI object of type MPIVariables

Definition at line 37 of file MPIIOGroups.c.

 {
   MPIVariables *mpi = (MPIVariables*) m;
 
 #ifndef serial
 
   int nproc         = mpi->nproc;
   int rank          = mpi->rank;
   int N_IORanks     = mpi->N_IORanks;
 
   int GroupSize;
   if (nproc%N_IORanks==0) GroupSize = nproc/N_IORanks;
   else {
     if (!rank) {
       printf("Note: in MPICreateIOGroups() - Number of ");
       printf("ranks (nproc) is not divisible by number ");
       printf("of IO ranks (N_IORanks). Readjusting number ");
       printf("of IO ranks to fix this.\n");
     }
     N_IORanks = 1;
     if (!rank) {
       printf("Number of IO Ranks: %d\n",N_IORanks);
     }
     GroupSize = nproc;
   }
 
   mpi->CommGroup  = rank/GroupSize;
   mpi->IORank     = mpi->CommGroup * GroupSize;
 
   /* set flag for whether this rank does file I/O */
   if (rank == mpi->IORank)  mpi->IOParticipant = 1;
   else                      mpi->IOParticipant = 0;
 
   /* save the first and last process of this group */
   mpi->GroupStartRank = mpi->IORank;
   mpi->GroupEndRank   = (mpi->CommGroup+1)*GroupSize;
 
   /* create a new communicator with the IO participants */
   int i,*FileIORanks;
   MPI_Group WorldGroup, IOGroup;
   FileIORanks = (int*) calloc (N_IORanks,sizeof(int));
   for (i=0; i<N_IORanks; i++) FileIORanks[i] = i*GroupSize;
   MPI_Comm_group(mpi->world,&WorldGroup);
   MPI_Group_incl(WorldGroup,N_IORanks,FileIORanks,&IOGroup);
   MPI_Comm_create(mpi->world,IOGroup,&mpi->IOWorld);
   MPI_Group_free(&IOGroup);
   MPI_Group_free(&WorldGroup);
   free(FileIORanks);
 
 #endif
 
   return(0);
 }

int MPIExchangeBoundaries1D	(	void *	m,
		double *	x,
		int	N,
		int	ghosts,
		int	dir,
		int	ndims
	)

Exchange boundary (ghost point) values for an essentially 1D array (like grid coordinates)

Exchange the data across MPI ranks and fill in ghost points for a 1D array. In a multidimensional simulation, a 1D array is an array of data along one of the spatial dimensions, i.e. its an array storing a variable that varies in only one of the spatial dimension. For example, for a 2D problem on a Cartesian grid (with spatial dimensions x and y), the array of x-coordinates is a 1D array along x, and the array of y-coordinates is a 1D array along y. Thus, the size of the 1D array is equal to the size of the domain along the spatial dimension corresponding to that array.

Consider a two-dimensional problem, partitioned on 21 MPI ranks as follows:

and consider rank 9.

If the argument dir is specified as 0, and thus we are dealing with a 1D array along dimension 0, then

Rank 9 will exchange data with ranks 8 and 10, and fill in its ghost points.

If dir is specified as 1, and thus we are dealing with a 1D array along dimension 1, then

Rank 9 will exchange data with ranks 2 and 16, and fill in its ghost points.

Parameters

m	MPI object of type MPIVariables
x	The 1D array for which to exchange data
N	Size of the array
ghosts	Number of ghost points
dir	Spatial dimension corresponding to the 1D array
ndims	Number of spatial dimensions in the simulation

Definition at line 32 of file MPIExchangeBoundaries1D.c.

 {
 #ifndef serial
   MPIVariables  *mpi = (MPIVariables*) m;
   int           i;
   
   int *ip     = mpi->ip;
   int *iproc  = mpi->iproc;
   int non      = 0; /* number of neighbours */
 
   int neighbor_rank[2] = {-1,-1};
   int nip[ndims];
 
   /* each process has 2 neighbors (except at physical boundaries)       */
   /* calculate the rank of these neighbors (-1 -> none)                 */
   _ArrayCopy1D_(ip,nip,ndims);  nip[dir]--;
   if (ip[dir] == 0)             neighbor_rank[0] = -1;
   else                          neighbor_rank[0] = MPIRank1D(ndims,iproc,nip);
   _ArrayCopy1D_(ip,nip,ndims);  nip[dir]++;
   if (ip[dir] == (iproc[dir]-1))neighbor_rank[1] = -1;
   else                          neighbor_rank[1] = MPIRank1D(ndims,iproc,nip);
 
   /* Allocate send and receive buffers */
   double sendbuf[2][ghosts], recvbuf[2][ghosts];
 
   /* count number of neighbors and copy data to send buffers */
   non = 0;
   if (neighbor_rank[0] != -1) {
     non++;
     for (i = 0; i < ghosts; i++) sendbuf[0][i] = x[i+ghosts];
   }
   if (neighbor_rank[1] != -1) {
     non++;
     for (i = 0; i < ghosts; i++) sendbuf[1][i] = x[i+N];
   }
   MPI_Request requests[2*non];
   MPI_Status  statuses[2*non];
 
   /* exchange the data */
   int tick = 0;
   if (neighbor_rank[0]!= -1) {
     MPI_Irecv(recvbuf[0],ghosts,MPI_DOUBLE,neighbor_rank[0],1631,mpi->world,&requests[tick]);
     MPI_Isend(sendbuf[0],ghosts,MPI_DOUBLE,neighbor_rank[0],1631,mpi->world,&requests[tick+non]);
     tick++;
   }
   if (neighbor_rank[1] != -1) {
     MPI_Irecv(recvbuf[1],ghosts,MPI_DOUBLE,neighbor_rank[1],1631,mpi->world,&requests[tick]);
     MPI_Isend(sendbuf[1],ghosts,MPI_DOUBLE,neighbor_rank[1],1631,mpi->world,&requests[tick+non]);
     tick++;
   }
 
   /* Wait till data transfer is done */
   MPI_Waitall(2*non,requests,statuses);
 
   /* copy received data to ghost points */
   if (neighbor_rank[0] != -1) for (i = 0; i < ghosts; i++) x[i]          = recvbuf[0][i];
   if (neighbor_rank[1] != -1) for (i = 0; i < ghosts; i++) x[i+N+ghosts] = recvbuf[1][i];
   
 #endif
   return(0);
 }

int MPIExchangeBoundariesnD	(	int	ndims,
		int	nvars,
		int *	dim,
		int	ghosts,
		void *	m,
		double *	var
	)

Exchange boundary (ghost point) values for an n-dimensional array (like the solution array)

Exchange data across MPI ranks, and fill in ghost points for an n-dimensional array (where n is the total number of spatial dimensions). If any of the physical boundaries are periodic, this function also exchanges data and fills in the ghost points for these boundaries.

The n-dimensional array must be stored in the memory as a single-index array, with the following order of mapping:

Number of variables (vector components)
Spatial dimension 0
Spatial dimension 1
...
Spatial dimensions ndims-1

For example, consider a 2D simulation (ndims = 2), of size \(7 \times 3\), with \(4\) vector components (nvars = 4). The following figure shows the layout (without the ghost points):

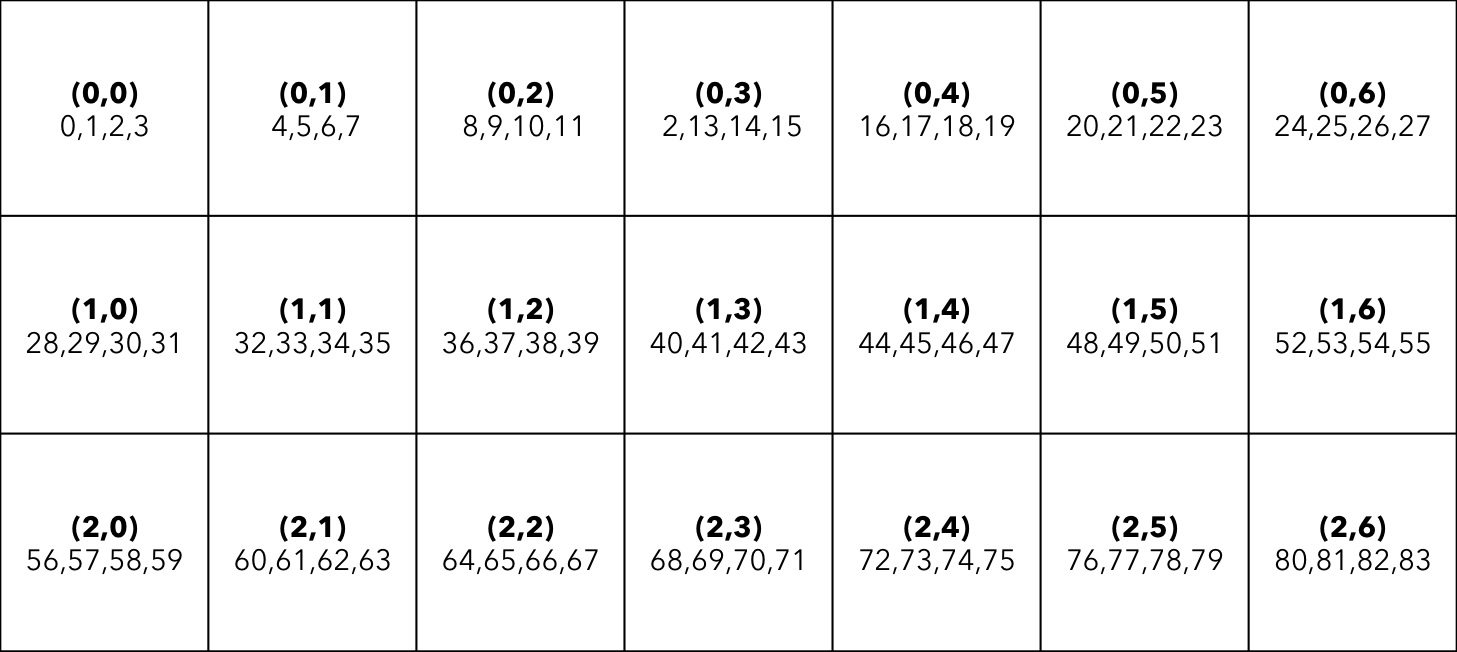
The bold numbers in parentheses represent the 2D indices. The numbers below them are the indices of the array that correspond to that 2D location. Thus, elements 40,41,42, and 43 in the array are the 1st, 2nd, 3rd, and 4th vector components at location (1,3).

If \({\bf i}\left[{\rm ndims}\right]\) is an integer array representing an n-dimensional index (for example, \(\left(5,4\right)\) in 2D, \(\left(3,5,2\right)\) in 3D), and the number of vector components is nvars, then:

_ArrayIndex1D_ computes the index \(p\) in the array corresponding to \({\bf i}\). In the above example, \({\bf i} = \left(1,3\right) \rightarrow p = 10\).
var[nvars*p+v] accesses the v-th component of the n-dimensional array var at location \({\bf i}\). In the above example, to access the 3rd vector component at location \(\left(1,3\right)\), we have \(p=10\), so var [4*10+2] = var [42].

Parameters

ndims	Number of spatial dimensions
nvars	Number of variables (vector components) at each grid location
dim	Integer array whose elements are the local size along each spatial dimension
ghosts	Number of ghost points
m	MPI object of type MPIVariables
var	The array for which to exchange data and fill in ghost points

Definition at line 42 of file MPIExchangeBoundariesnD.c.

 {
 #ifndef serial
   MPIVariables  *mpi = (MPIVariables*) m;
   int           d;
   
   int *ip     = mpi->ip;
   int *iproc  = mpi->iproc;
   int *bcflag = mpi->bcperiodic;
 
   int neighbor_rank[2*ndims], nip[ndims], index[ndims], bounds[ndims], offset[ndims];
   MPI_Request rcvreq[2*ndims], sndreq[2*ndims];
   for (d=0; d<2*ndims; d++) rcvreq[d] = sndreq[d] = MPI_REQUEST_NULL;
 
   /* each process has 2*ndims neighbors (except at non-periodic physical boundaries)  */
   /* calculate the rank of these neighbors (-1 -> none)                               */
   for (d = 0; d < ndims; d++) {
     _ArrayCopy1D_(ip,nip,ndims); 
     if (ip[d] == 0) nip[d] = iproc[d]-1;
     else            nip[d]--;
     if ((ip[d] == 0) && (!bcflag[d])) neighbor_rank[2*d]   = -1;
     else                              neighbor_rank[2*d]   = MPIRank1D(ndims,iproc,nip);
     _ArrayCopy1D_(ip,nip,ndims); 
     if (ip[d] == (iproc[d]-1)) nip[d] = 0;
     else                       nip[d]++;
     if ((ip[d] == (iproc[d]-1)) && (!bcflag[d]))  neighbor_rank[2*d+1] = -1;
     else                                          neighbor_rank[2*d+1] = MPIRank1D(ndims,iproc,nip);
   }
 
   /* calculate dimensions of each of the send-receive regions */
   double *sendbuf = mpi->sendbuf;
   double *recvbuf = mpi->recvbuf;
   int    stride   = mpi->maxbuf;
   int    bufdim[ndims];
   for (d = 0; d < ndims; d++) {
     bufdim[d] = 1;
     int i;
     for (i = 0; i < ndims; i++) {
       if (i == d) bufdim[d] *= ghosts;
       else        bufdim[d] *= dim[i];
     }
   }
 
   /* post the receive requests */
   for (d = 0; d < ndims; d++) {
     if (neighbor_rank[2*d  ] != -1) {
       MPI_Irecv(&recvbuf[2*d*stride],bufdim[d]*nvars,MPI_DOUBLE,neighbor_rank[2*d  ],1630,
                 mpi->world,&rcvreq[2*d]);
     }
     if (neighbor_rank[2*d+1] != -1) {
       MPI_Irecv(&recvbuf[(2*d+1)*stride],bufdim[d]*nvars,MPI_DOUBLE,neighbor_rank[2*d+1],1631,
                 mpi->world,&rcvreq[2*d+1]);
     }
   }
 
   /* count number of neighbors and copy data to send buffers */
   for (d = 0; d < ndims; d++) {
     _ArrayCopy1D_(dim,bounds,ndims); bounds[d] = ghosts;
     if (neighbor_rank[2*d] != -1) {
       _ArraySetValue_(offset,ndims,0);
       int done = 0; _ArraySetValue_(index,ndims,0);
       while (!done) {
         int p1; _ArrayIndex1DWO_(ndims,dim,index,offset,ghosts,p1);
         int p2; _ArrayIndex1D_(ndims,bounds,index,0,p2);
         _ArrayCopy1D_((var+nvars*p1),(sendbuf+2*d*stride+nvars*p2),nvars);
         _ArrayIncrementIndex_(ndims,bounds,index,done);
       }
     }
     if (neighbor_rank[2*d+1] != -1) {
       _ArraySetValue_(offset,ndims,0);offset[d] = dim[d]-ghosts;
       int done = 0; _ArraySetValue_(index,ndims,0);
       while (!done) {
         int p1; _ArrayIndex1DWO_(ndims,dim,index,offset,ghosts,p1);
         int p2; _ArrayIndex1D_(ndims,bounds,index,0,p2);
         _ArrayCopy1D_((var+nvars*p1),(sendbuf+(2*d+1)*stride+nvars*p2),nvars);
         _ArrayIncrementIndex_(ndims,bounds,index,done);
       }
     }
   }
 
   /* send the data */
   for (d = 0; d < ndims; d++) {
     if (neighbor_rank[2*d  ] != -1) {
       MPI_Isend(&sendbuf[2*d*stride],bufdim[d]*nvars,MPI_DOUBLE,neighbor_rank[2*d  ],1631,
                 mpi->world,&sndreq[2*d]);
     }
     if (neighbor_rank[2*d+1] != -1) {
       MPI_Isend(&sendbuf[(2*d+1)*stride],bufdim[d]*nvars,MPI_DOUBLE,neighbor_rank[2*d+1],1630,
                 mpi->world,&sndreq[2*d+1]);
     }
   }
 
   /* Wait till data is done received */
   MPI_Status status_arr[2*ndims];
   MPI_Waitall(2*ndims,rcvreq,status_arr);
   /* copy received data to ghost points */
   for (d = 0; d < ndims; d++) {
     _ArrayCopy1D_(dim,bounds,ndims); bounds[d] = ghosts;
     if (neighbor_rank[2*d] != -1) {
       _ArraySetValue_(offset,ndims,0); offset[d] = -ghosts;
       int done = 0; _ArraySetValue_(index,ndims,0);
       while (!done) {
         int p1; _ArrayIndex1DWO_(ndims,dim,index,offset,ghosts,p1);
         int p2; _ArrayIndex1D_(ndims,bounds,index,0,p2);
         _ArrayCopy1D_((recvbuf+2*d*stride+nvars*p2),(var+nvars*p1),nvars);
         _ArrayIncrementIndex_(ndims,bounds,index,done);
       }
     }
     if (neighbor_rank[2*d+1] != -1) {
       _ArraySetValue_(offset,ndims,0); offset[d] = dim[d];
       int done = 0; _ArraySetValue_(index,ndims,0);
       while (!done) {
         int p1; _ArrayIndex1DWO_(ndims,dim,index,offset,ghosts,p1);
         int p2; _ArrayIndex1D_(ndims,bounds,index,0,p2);
         _ArrayCopy1D_((recvbuf+(2*d+1)*stride+nvars*p2),(var+nvars*p1),nvars);
         _ArrayIncrementIndex_(ndims,bounds,index,done);
       }
     }
   }
   /* Wait till send requests are complete before freeing memory */
   MPI_Waitall(2*ndims,sndreq,status_arr);
 
 #endif
   return(0);
 }

int MPIGatherArray1D	(	void *	m,
		double *	xg,
		double *	x,
		int	istart,
		int	iend,
		int	N_local,
		int	ghosts
	)

Gather local arrays into a global array for an essentially 1D array

Gathers the contents of a 1D array (partitioned amongst MPI ranks) into a global 1D array on the root rank (rank 0). See documentation of MPIExchangeBoundaries1D() on what a "1D array" is in the context of a multidimensional simulation. The 1D array must be the same along spatial dimensions normal to the one it represents.

Notes:

The global array must not have ghost points.
The global array must be preallocated on only rank 0. On other ranks, it must be NULL.
Since this function deals with a 1D array, more than one rank may be sending the same piece of data to rank 0 (i.e. if there are more than one MPI rank along the dimensions normal to one corresponding to x ). The implementation of this function ignores this and overwrites that portion with the latest data sent.

Parameters

m	MPI object of type MPIVariables
xg	Global 1D array (must be preallocated) without ghost points
x	Local 1D array to be gathered
istart	Starting index (global) of this rank's portion of the array
iend	Ending index (global) of this rank's portion of the array + 1
N_local	Local size of the array
ghosts	Number of ghost points

Definition at line 26 of file MPIGatherArray1D.c.

 {
   MPIVariables *mpi = (MPIVariables*) m;
   int          ierr = 0;
 
   /* xg should be non-null only on root */
   if (mpi->rank && xg) {
     fprintf(stderr,"Error in MPIGatherArray1D(): global array exists on non-root processors (rank %d).\n",
             mpi->rank);
     ierr = 1;
   }
   if ((!mpi->rank) && (!xg)) {
     fprintf(stderr,"Error in MPIGatherArray1D(): global array is not allocated on root processor.\n");
     ierr = 1;
   }
 
   /* create and copy data to a buffer to send to the root process */
   double *buffer = (double*) calloc (N_local,sizeof(double));
   _ArrayCopy1D_((x+ghosts),(buffer),N_local);
 
   if (!mpi->rank) {
 #ifndef serial
     MPI_Status status;
 #endif
     int proc;
     for (proc = 0; proc < mpi->nproc; proc++) {
       /* Find out the domain limits for each process */
       int is,ie;
       if (proc) {
 #ifndef serial
         MPI_Recv(&is,1,MPI_INT,proc,1442,mpi->world,&status);
         MPI_Recv(&ie,1,MPI_INT,proc,1443,mpi->world,&status);
 #endif
       } else { is = istart; ie = iend; }
       int size = ie - is;
       if (proc) {
 #ifndef serial
         double *recvbuf = (double*) calloc (size,sizeof(double));
         MPI_Recv(recvbuf,size,MPI_DOUBLE,proc,1916,mpi->world,&status);
         _ArrayCopy1D_((recvbuf),(xg+is),size);
         free(recvbuf);
 #endif
       } else _ArrayCopy1D_(buffer,(xg+is),size);
     }
 
   } else {
 #ifndef serial
     /* Meanwhile, on other processes - send stuff to root */
     MPI_Send(&istart,1      ,MPI_INT   ,0,1442,mpi->world);
     MPI_Send(&iend  ,1      ,MPI_INT   ,0,1443,mpi->world);
     MPI_Send(buffer ,N_local,MPI_DOUBLE,0,1916,mpi->world);
 #endif
   }
 
   free(buffer);
   return(ierr);
 }

int MPIGatherArraynD	(	int	ndims,
		void *	m,
		double *	xg,
		double *	x,
		int *	dim_global,
		int *	dim_local,
		int	ghosts,
		int	nvars
	)

Gather local arrays into a global array for an n-dimensional array

Gathers the contents of an n-dimensional array, partitioned amongst the MPI ranks, in to a global array on rank 0. See documentation of MPIExchangeBoundariesnD() for how the n-dimensional array is stored in the memory as a single-index array.

Notes:

The global array must have no ghost points.
The global array must be allocated only on rank 0. On other ranks, it must be NULL.

Parameters

ndims	Number of spatial dimensions
m	MPI object of type MPIVariables
xg	Global array (preallocated) without ghost points
x	Local array
dim_global	Integer array with elements as global size along each spatial dimension
dim_local	Integer array with elements as local size along each spatial dimension
ghosts	Number of ghost points
nvars	Number of variables (vector components)

Definition at line 21 of file MPIGatherArraynD.c.

 {
   MPIVariables *mpi = (MPIVariables*) m;
   int          d, size;
   _DECLARE_IERR_;
 
   int is[ndims], ie[ndims], index[ndims], bounds[ndims];
 
   /* xg should be non-null only on root */
   if (mpi->rank && xg) {
     fprintf(stderr,"Error in MPIGatherArraynD(): global array exists on non-root processors (rank %d).\n",
             mpi->rank);
     return(1);
   }
   if ((!mpi->rank) && (!xg)) {
     fprintf(stderr,"Error in MPIGatherArraynD(): global array is not allocated on root processor.\n");
     return(1);
   }
 
   /* calculate total size of local domain (w/o ghosts) */
   size = 1;
   for (d = 0; d < ndims; d++) size *= dim_local[d];
 
   /* create and copy data to send to root process */
   double *buffer = (double*) calloc (size*nvars, sizeof(double));
   IERR ArrayCopynD(ndims,x,buffer,dim_local,ghosts,0,index,nvars); CHECKERR(ierr);
 
   if (!mpi->rank) {
     int proc;
     for (proc = 0; proc < mpi->nproc; proc++) {
       int d,done,size;
       /* Find out the domain limits for each process */
       IERR MPILocalDomainLimits(ndims,proc,mpi,dim_global,is,ie); CHECKERR(ierr);
       size = 1;
       for (d=0; d<ndims; d++) {
         size *= (ie[d]-is[d]);
         bounds[d] = ie[d] - is[d];
       }
       if (proc) {
 #ifndef serial
         MPI_Status status;
         double *recvbuf = (double*) calloc (size*nvars, sizeof(double));
         MPI_Recv(recvbuf,size*nvars,MPI_DOUBLE,proc,1902,mpi->world,&status);
         int done = 0; _ArraySetValue_(index,ndims,0);
         while (!done) {
           int p1; _ArrayIndex1D_(ndims,bounds,index,0,p1);
           int p2; _ArrayIndex1DWO_(ndims,dim_global,index,is,0,p2);
           _ArrayCopy1D_((recvbuf+nvars*p1),(xg+nvars*p2),nvars);
           _ArrayIncrementIndex_(ndims,bounds,index,done);
         }
         free(recvbuf);
 #endif
       } else {
         done = 0; _ArraySetValue_(index,ndims,0);
         while (!done) {
           int p1; _ArrayIndex1D_(ndims,bounds,index,0,p1);
           int p2; _ArrayIndex1DWO_(ndims,dim_global,index,is,0,p2);
           _ArrayCopy1D_((buffer+nvars*p1),(xg+nvars*p2),nvars);
           _ArrayIncrementIndex_(ndims,bounds,index,done);
         }
       }
     }
 
   } else {
 #ifndef serial
     /* Meanwhile, on other processes */
     MPI_Send(buffer,size*nvars,MPI_DOUBLE,0,1902,mpi->world);
 #endif
   }
 
   free(buffer);
   return(0);
 }

int MPIGatherArraynDwGhosts	(	int	ndims,
		void *	m,
		double *	xg,
		double *	x,
		int *	dim_global,
		int *	dim_local,
		int	ghosts,
		int	nvars
	)

Gather local arrays into a global array for an n-dimensional array (with ghosts)

Gathers the contents of an n-dimensional array, partitioned amongst the MPI ranks, in to a global array on rank 0. See documentation of MPIExchangeBoundariesnD() for how the n-dimensional array is stored in the memory as a single-index array. This is same as MPIGatherArraynD() but where the global array has ghost points.

Notes:

The global array must have ghost points (the same number as the local arrays).
The global array must be allocated only on rank 0. On other ranks, it must be NULL.

Parameters

ndims	Number of spatial dimensions
m	MPI object of type MPIVariables
xg	Global array (preallocated) with ghost points
x	Local array
dim_global	Integer array with elements as global size along each spatial dimension
dim_local	Integer array with elements as local size along each spatial dimension
ghosts	Number of ghost points
nvars	Number of variables (vector components)

Definition at line 115 of file MPIGatherArraynD.c.

 {
   MPIVariables *mpi = (MPIVariables*) m;
   int          d, size;
   _DECLARE_IERR_;
 
   /* do an exchange to make sure interior/periodic ghost points are filled with consistent values */
   IERR MPIExchangeBoundariesnD(ndims, nvars, dim_local, ghosts, mpi, x);
 
   int is[ndims], ie[ndims], index[ndims], bounds[ndims];
   int dim_global_wghosts[ndims];
   for (d = 0; d < ndims; d++) dim_global_wghosts[d] = dim_global[d] + 2*ghosts;
 
   /* xg should be non-null only on root */
   if (mpi->rank && xg) {
     fprintf(stderr,"Error in MPIGatherArraynD(): global array exists on non-root processors (rank %d).\n",
             mpi->rank);
     return(1);
   }
   if ((!mpi->rank) && (!xg)) {
     fprintf(stderr,"Error in MPIGatherArraynD(): global array is not allocated on root processor.\n");
     return(1);
   }
 
   /* calculate total size of local domain (w/ ghosts) */
   size = 1;
   for (d = 0; d < ndims; d++) size *= (dim_local[d]+2*ghosts);
 
   /* create and copy data (incl. ghost points) to send to root process */
   double *buffer = (double*) calloc (size*nvars, sizeof(double));
   _ArrayCopy1D_(x, buffer, size*nvars);
 
   if (!mpi->rank) {
     int proc;
     for (proc = 0; proc < mpi->nproc; proc++) {
       int d,done;
       /* Find out the domain limits for each process */
       IERR MPILocalDomainLimits(ndims,proc,mpi,dim_global,is,ie); CHECKERR(ierr);
       for (d=0; d<ndims; d++) {
         bounds[d] = ie[d] - is[d];
       }
       if (proc) {
 #ifndef serial
         int size = 1;
         for (d=0; d<ndims; d++) {
           size *= (ie[d]-is[d]+2*ghosts);
           bounds[d] = ie[d] - is[d];
         }
         MPI_Status status;
         double *recvbuf = (double*) calloc (size*nvars, sizeof(double));
         MPI_Recv(recvbuf,size*nvars,MPI_DOUBLE,proc,1902,mpi->world,&status);
         int done = 0; _ArraySetValue_(index,ndims,0);
         while (!done) {
           int p1; _ArrayIndex1D_(ndims,bounds,index,ghosts,p1);
           int p2; _ArrayIndex1DWO_(ndims,dim_global,index,is,ghosts,p2);
           _ArrayCopy1D_((recvbuf+nvars*p1),(xg+nvars*p2),nvars);
           _ArrayIncrementIndex_(ndims,bounds,index,done);
         }
         free(recvbuf);
 #endif
       } else {
         done = 0; _ArraySetValue_(index,ndims,0);
         while (!done) {
           int p1; _ArrayIndex1D_(ndims,bounds,index,ghosts,p1);
           int p2; _ArrayIndex1DWO_(ndims,dim_global,index,is,ghosts,p2);
           _ArrayCopy1D_((buffer+nvars*p1),(xg+nvars*p2),nvars);
           _ArrayIncrementIndex_(ndims,bounds,index,done);
         }
       }
     }
 
   } else {
 #ifndef serial
     /* Meanwhile, on other processes */
     MPI_Send(buffer,size*nvars,MPI_DOUBLE,0,1902,mpi->world);
 #endif
   }
 
   free(buffer);
   return(0);
 }

int MPIPartitionArraynD	(	int	ndims,
		void *	m,
		double *	xg,
		double *	x,
		int *	dim_global,
		int *	dim_local,
		int	ghosts,
		int	nvars
	)

Partition a global array into local arrays for an n-dimensional array

Partitions the contents of a global n-dimensional array on rank 0 (root) to local n-dimensional arrays on all the MPI ranks. See documentation of MPIExchangeBoundariesnD() for how the n-dimensional array is stored in the memory as a single-index array.

Notes:

The global array must have no ghost points.
The global array must be allocated only on rank 0. On other ranks, it must be NULL.

Parameters

ndims	Number of spatial dimensions
m	MPI object of type MPIVariables
xg	Global array (preallocated) without ghost points
x	Local array
dim_global	Integer array with elements as global size along each spatial dimension
dim_local	Integer array with elements as local size along each spatial dimension
ghosts	Number of ghost points
nvars	Number of variables (vector components)

Definition at line 21 of file MPIPartitionArraynD.c.

 {
   MPIVariables *mpi = (MPIVariables*) m;
   _DECLARE_IERR_;
 
   int is[ndims], ie[ndims], index[ndims], bounds[ndims];
 
   /* xg should be non-null only on root */
   if (mpi->rank && xg) {
     fprintf(stderr,"Error in MPIPartitionArraynD(): global array exists on non-root processors (rank %d).\n",
             mpi->rank);
     return(1);
   }
   if ((!mpi->rank) && (!xg)) {
     fprintf(stderr,"Error in MPIPartitionArraynD(): global array is not allocated on root processor.\n");
     return(1);
   }
 
   if (!mpi->rank) {
     int proc;
     for (proc = 0; proc < mpi->nproc; proc++) {
       int d,done,size;
       /* Find out the domain limits for each process */
       IERR MPILocalDomainLimits(ndims,proc,mpi,dim_global,is,ie); CHECKERR(ierr);
       size = 1;
       for (d=0; d<ndims; d++) {
         size *= (ie[d]-is[d]);
         bounds[d] = ie[d] - is[d];
       }
       double *buffer = (double*) calloc (size*nvars, sizeof(double));
       done = 0; _ArraySetValue_(index,ndims,0);
       while (!done) {
         int p1; _ArrayIndex1DWO_(ndims,dim_global,index,is,0,p1);
         int p2; _ArrayIndex1D_(ndims,bounds,index,0,p2);
         _ArrayCopy1D_((xg+nvars*p1),(buffer+nvars*p2),nvars);
         _ArrayIncrementIndex_(ndims,bounds,index,done);
       }
       if (proc) {
 #ifndef serial
         MPI_Send(buffer,size*nvars,MPI_DOUBLE,proc,1538,mpi->world);
 #endif
       } else {
         done = 0; _ArraySetValue_(index,ndims,0);
         while (!done) {
           int p1; _ArrayIndex1D_(ndims,dim_local,index,ghosts,p1);
           int p2; _ArrayIndex1D_(ndims,dim_local,index,0,p2);
           _ArrayCopy1D_((buffer+nvars*p2),(x+nvars*p1),nvars);
           _ArrayIncrementIndex_(ndims,dim_local,index,done);
         }
       }
       free(buffer);
     }
 
   } else {
 #ifndef serial
     /* Meanwhile, on other processes */
     MPI_Status  status;
     int d, done, size;
     size = 1; for (d=0; d<ndims; d++) size *= dim_local[d];
     double *buffer = (double*) calloc (size*nvars, sizeof(double));
     MPI_Recv(buffer,size*nvars,MPI_DOUBLE,0,1538,mpi->world,&status);
     done = 0; _ArraySetValue_(index,ndims,0);
     while (!done) {
       int p1; _ArrayIndex1D_(ndims,dim_local,index,ghosts,p1);
       int p2; _ArrayIndex1D_(ndims,dim_local,index,0,p2);
       _ArrayCopy1D_((buffer+nvars*p2),(x+nvars*p1),nvars);
       _ArrayIncrementIndex_(ndims,dim_local,index,done);
     }
     free(buffer);
 #endif
   }
   return(0);
 }

int MPIPartitionArraynDwGhosts	(	int	ndims,
		void *	m,
		double *	xg,
		double *	x,
		int *	dim_global,
		int *	dim_local,
		int	ghosts,
		int	nvars
	)

Partition a global array into local arrays for an n-dimensional array

Partitions the contents of a global n-dimensional array on rank 0 (root) to local n-dimensional arrays on all the MPI ranks. See documentation of MPIExchangeBoundariesnD() for how the n-dimensional array is stored in the memory as a single-index array. This is same as MPIPartitionArraynD() but where the global array has ghost points.

Notes:

The global array must have ghost points (the same number as the local arrays).
The global array must be allocated only on rank 0. On other ranks, it must be NULL.

Parameters

ndims	Number of spatial dimensions
m	MPI object of type MPIVariables
xg	Global array (preallocated) without ghost points
x	Local array
dim_global	Integer array with elements as global size along each spatial dimension
dim_local	Integer array with elements as local size along each spatial dimension
ghosts	Number of ghost points
nvars	Number of variables (vector components)

Definition at line 114 of file MPIPartitionArraynD.c.

 {
   MPIVariables *mpi = (MPIVariables*) m;
   int d;
   _DECLARE_IERR_;
 
   int is[ndims], ie[ndims], index[ndims], bounds[ndims];
   int dim_global_wghosts[ndims];
   for (d = 0; d < ndims; d++) dim_global_wghosts[d] = dim_global[d] + 2*ghosts;
 
   /* xg should be non-null only on root */
   if (mpi->rank && xg) {
     fprintf(stderr,"Error in MPIPartitionArraynD(): global array exists on non-root processors (rank %d).\n",
             mpi->rank);
     return(1);
   }
   if ((!mpi->rank) && (!xg)) {
     fprintf(stderr,"Error in MPIPartitionArraynD(): global array is not allocated on root processor.\n");
     return(1);
   }
 
   if (!mpi->rank) {
     int proc;
     for (proc = 0; proc < mpi->nproc; proc++) {
       int done,size;
       /* Find out the domain limits for each process */
       IERR MPILocalDomainLimits(ndims,proc,mpi,dim_global,is,ie); CHECKERR(ierr);
       size = 1;
       for (d=0; d<ndims; d++) {
         size *= (ie[d]-is[d]+2*ghosts);
         bounds[d] = ie[d] - is[d] + 2*ghosts;
       }
       double *buffer = (double*) calloc (size*nvars, sizeof(double));
       done = 0; _ArraySetValue_(index,ndims,0);
       while (!done) {
         int p1; _ArrayIndex1DWO_(ndims,dim_global_wghosts,index,is,0,p1);
         int p2; _ArrayIndex1D_(ndims,bounds,index,0,p2);
         _ArrayCopy1D_((xg+nvars*p1),(buffer+nvars*p2),nvars);
         _ArrayIncrementIndex_(ndims,bounds,index,done);
       }
       if (proc) {
 #ifndef serial
         MPI_Send(buffer,size*nvars,MPI_DOUBLE,proc,1538,mpi->world);
 #endif
       } else {
         done = 0; _ArraySetValue_(index,ndims,0);
         _ArrayCopy1D_(buffer, x, size*nvars);
       }
       free(buffer);
     }
 
   } else {
 #ifndef serial
     /* Meanwhile, on other processes */
     MPI_Status  status;
     int done, size;
     size = 1; for (d=0; d<ndims; d++) size *= (dim_local[d]+2*ghosts);
     double *buffer = (double*) calloc (size*nvars, sizeof(double));
     MPI_Recv(buffer,size*nvars,MPI_DOUBLE,0,1538,mpi->world,&status);
     _ArrayCopy1D_(buffer, x, size*nvars);
     free(buffer);
 #endif
   }
   return(0);
 }

int MPIPartitionArray1D	(	void *	m,
		double *	xg,
		double *	x,
		int	istart,
		int	iend,
		int	N_local,
		int	ghosts
	)

Partition a global array into local arrays for an essentially 1D array

Partitions the contents of a global 1D array on the root rank (rank 0) to local arrays on all the MPI ranks. See documentation of MPIExchangeBoundaries1D() on what a "1D array" is in the context of a multidimensional simulation. The 1D array must be the same along spatial dimensions normal to the one it represents.

Notes:

The global array must not have ghost points.
The global array must be preallocated on only rank 0. On other ranks, it must be NULL.
Since this function deals with a 1D array, more than one rank may be receiving the same piece of data from rank 0 (i.e. if there are more than one MPI rank along the dimensions normal to one corresponding to x ).

Parameters

m	MPI object of type MPIVariables
xg	Global 1D array (must be preallocated) without ghost points
x	Local 1D array to be gathered
istart	Starting index (global) of this rank's portion of the array
iend	Ending index (global) of this rank's portion of the array + 1
N_local	Local size of the array
ghosts	Number of ghost points

Definition at line 25 of file MPIPartitionArray1D.c.

 {
   MPIVariables *mpi = (MPIVariables*) m;
   int          ierr = 0;
 #ifndef serial
   MPI_Status   status;
 #endif
 
   /* xg should be non-null only on root */
   if (mpi->rank && xg) {
     fprintf(stderr,"Error in MPIPartitionArray1D(): global array exists on non-root processors (rank %d).\n",
             mpi->rank);
     ierr = 1;
   }
   if ((!mpi->rank) && (!xg)) {
     fprintf(stderr,"Error in MPIPartitionArray1D(): global array is not allocated on root processor.\n");
     ierr = 1;
   }
 
   if (!mpi->rank) {
     int proc;
     for (proc = 0; proc < mpi->nproc; proc++) {
       /* Find out the domain limits for each process */
       int is,ie;
       if (proc) {
 #ifndef serial
         MPI_Recv(&is,1,MPI_INT,proc,1442,mpi->world,&status);
         MPI_Recv(&ie,1,MPI_INT,proc,1443,mpi->world,&status);
 #endif
       } else {
         is = istart;
         ie = iend;
       }
       int size = ie - is;
       double *buffer = (double*) calloc (size, sizeof(double));
       _ArrayCopy1D_((xg+is),buffer,size);
       if (proc) {
 #ifndef serial
         MPI_Send(buffer,size,MPI_DOUBLE,proc,1539,mpi->world);
 #endif
       } else _ArrayCopy1D_(buffer,x,N_local);
       free(buffer);
     }
 
   } else {
 #ifndef serial
     /* Meanwhile, on other processes */
     /* send local start and end indices to root */
     MPI_Send(&istart,1,MPI_INT,0,1442,mpi->world);
     MPI_Send(&iend  ,1,MPI_INT,0,1443,mpi->world);
     double *buffer = (double*) calloc (N_local, sizeof(buffer));
     MPI_Recv(buffer,N_local,MPI_DOUBLE,0,1539,mpi->world,&status);
     _ArrayCopy1D_(buffer,x,N_local);
     free(buffer);
 #endif
   }
   return(ierr);
 }

int MPIGetArrayDatanD	(	double *	xbuf,
		double *	x,
		int *	source,
		int *	dest,
		int *	limits,
		int *	dim,
		int	ghosts,
		int	ndims,
		int	nvars,
		void *	m
	)

fetch data from an n-dimensional local array on another rank

This function lets one rank get a portion of a local n-dimensional array on another rank. The n-dimensional array must be stored in the memory as a single-index array as described in the documentation of MPIExchangeBoundariesnD(). The source rank sends to the dest rank a logically rectangular n-dimensional portion of its local copy of an array x. The extent of this logically rectangular portion is defined by limits.

limits is an array of size 2x the number of spatial dimensions, with elements as: [ is[0], ie[0], is[1], ie[1], ..., is[ndims-1], ie[ndims-1] ], where is[n] is the starting index along spatial dimension n, and ie[n] is the end index (+1) along spatial dimension n.

Parameters

xbuf	preallocated memory on destination rank to hold the received data
x	local array of which a part is needed
source	MPI rank of the source
dest	MPI rank of the destination
limits	Integer array (of size 2*ndims) with the start and end indices along each spatial dimension of the desired portion of the array
dim	Integer array whose elements are the local size of x in each spatial dimension
ghosts	Number of ghost points
ndims	Number of spatial dimensions
nvars	Number of variables (vector components)
m	MPI object of type MPIVariables

Definition at line 21 of file MPIGetArrayDatanD.c.

 {
   MPIVariables *mpi  = (MPIVariables*) m;
   int          d;
 
   int source_rank = MPIRank1D(ndims,mpi->iproc,source);
   int dest_rank   = MPIRank1D(ndims,mpi->iproc,dest  );
 
   int is[ndims], ie[ndims], index[ndims], bounds[ndims], size;
   size    = 1;
   for (d=0; d<ndims; d++) {
     is[d] =  limits[2*d  ];
     ie[d] =  limits[2*d+1];
     size  *= (ie[d] - is[d]);
   }
   _ArraySubtract1D_(bounds,ie,is,ndims);
 
   if (source_rank == dest_rank) {
     /* source and dest are the same process */
     int done = 0; _ArraySetValue_(index,ndims,0);
     while (!done) {
       int p1; _ArrayIndex1D_(ndims,bounds,index,0,p1);
       int p2; _ArrayIndex1DWO_(ndims,dim,index,is,ghosts,p2);
       _ArrayCopy1D_((x+nvars*p2),(xbuf+nvars*p1),nvars);
       _ArrayIncrementIndex_(ndims,bounds,index,done);
     }
   } else {
 #ifdef serial
     fprintf(stderr,"Error in MPIGetArrayDatanD(): This is a serial run. Source and ");
     fprintf(stderr,"destination ranks must be equal. Instead they are %d and %d.\n",
                     source_rank,dest_rank);
     return(1);
 #else
     if (mpi->rank == source_rank) {
       double *buf = (double*) calloc (size*nvars, sizeof(double));
       int done = 0; _ArraySetValue_(index,ndims,0);
       while (!done) {
         int p1; _ArrayIndex1D_(ndims,bounds,index,0,p1);
         int p2; _ArrayIndex1DWO_(ndims,dim,index,is,ghosts,p2);
         _ArrayCopy1D_((x+nvars*p2),(buf+nvars*p1),nvars);
         _ArrayIncrementIndex_(ndims,bounds,index,done);
       }
       MPI_Send(buf,size*nvars,MPI_DOUBLE,dest_rank,2211,mpi->world);
       free(buf);
     } else if (mpi->rank == dest_rank) {
       MPI_Status status;
       MPI_Recv(xbuf,size*nvars,MPI_DOUBLE,source_rank,2211,mpi->world,&status);
     } else {
       fprintf(stderr,"Error in MPIGetArrayData3D(): Process %d shouldn't have entered this function.\n",
               mpi->rank);
       return(1);
     }
 #endif
   }
   return(0);
 }

int MPILocalDomainLimits	(	int	ndims,
		int	p,
		void *	m,
		int *	dim_global,
		int *	is,
		int *	ie
	)

Calculate the local domain limits/extend in terms of the global domain

Computes the local domain limites: Given a MPI rank p, this function will compute the starting and ending indices of the local domain on this rank. These indices are global.

The starting and ending indices are stored in preallocated integer arrays, whose elements are these indices in each spatial dimension.
The ending index is 1 + actual last index; thus the one can write the loop as (i=start; i<end; i++) and not (i=start; i<=end; i++).

Parameters

ndims	Number of spatial dimensions
p	MPI rank
m	MPI object of type MPIVariables
dim_global	Integer array with elements as global size in each spatial dimension
is	Integer array whose elements will contain the starting index of the local domain on rank p
ie	Integer array whose elements will contain the ending index of the local domain on rank p

Definition at line 18 of file MPILocalDomainLimits.c.

 {
   MPIVariables *mpi = (MPIVariables*) m;
   int          i;
   _DECLARE_IERR_;
 
   int ip[ndims];
   IERR MPIRanknD(ndims,p,mpi->iproc,ip); CHECKERR(ierr);
 
   for (i=0; i<ndims; i++) {
     int imax_local, isize, root = 0;
     imax_local = MPIPartition1D(dim_global[i],mpi->iproc[i],root );
     isize      = MPIPartition1D(dim_global[i],mpi->iproc[i],ip[i]);
     if (is)  is[i] = ip[i]*imax_local;
     if (ie)  ie[i] = ip[i]*imax_local + isize;
   }
   return(0);
 }

int MPIMax_integer	(	int *	global,
		int *	var,
		int	size,
		void *	comm
	)

Find the maximum in an integer array over all ranks

Compute the global maximum over all MPI ranks in a given communicator for int datatype.

If var is an array of size greater than 1, global will be an array of the same size with each element as the maximum value of that element in var on all the MPI ranks in the given communicator.

Parameters

global	array to contain the global maximums
var	the local array
size	size of the local array
comm	MPI communicator

Definition at line 15 of file MPIMax.c.

 {
 #ifdef serial
   int i;
   for (i = 0; i < size; i++)  global[i] = var[i];
 #else
   MPI_Allreduce((var==global?MPI_IN_PLACE:var),global,size,MPI_INT,MPI_MAX,*((MPI_Comm*)comm));
 #endif
   return(0);
 }

int MPIMax_long	(	long *	,
		long *	,
		int	,
		void *
	)

Find the maximum in a long integer array over all ranks

int MPIMax_double	(	double *	global,
		double *	var,
		int	size,
		void *	comm
	)

Find the maximum in a double array over all ranks

Compute the global maximum over all MPI ranks in a given communicator for double datatype.

If var is an array of size greater than 1, global will be an array of the same size with each element as the maximum value of that element in var on all the MPI ranks in the given communicator.

Parameters

global	array to contain the global maximums
var	the local array
size	size of the local array
comm	MPI communicator

Definition at line 38 of file MPIMax.c.

 {
 #ifdef serial
   int i;
   for (i = 0; i < size; i++)  global[i] = var[i];
 #else
   MPI_Allreduce((var==global?MPI_IN_PLACE:var),global,size,MPI_DOUBLE,MPI_MAX,*((MPI_Comm*)comm));
 #endif
   return(0);
 }

int MPIMin_integer	(	int *	global,
		int *	var,
		int	size,
		void *	comm
	)

Find the minimum in an integer array over all ranks

Compute the global minimum over all MPI ranks in a given communicator for int datatype.

If var is an array of size greater than 1, global will be an array of the same size with each element as the minimum value of he that element in var on all the MPI ranks in the given communicator.

Parameters

global	array to contain the global minimums
var	the local array
size	size of the local array
comm	MPI communicator

Definition at line 15 of file MPIMin.c.

 {
 #ifdef serial
   int i;
   for (i = 0; i < size; i++)  global[i] = var[i];
 #else
   MPI_Allreduce((var==global?MPI_IN_PLACE:var),global,size,MPI_INT,MPI_MIN,*((MPI_Comm*)comm));
 #endif
   return(0);
 }

int MPIMin_double	(	double *	global,
		double *	var,
		int	size,
		void *	comm
	)

Find the minimum in a double array over all ranks

Compute the global minimum over all MPI ranks in a given communicator for double datatype.

If var is an array of size greater than 1, global will be an array of the same size with each element as the minimum value of that element in var on all the MPI ranks in the given communicator.

Parameters

global	array to contain the global minimums
var	the local array
size	size of the local array
comm	MPI communicator

Definition at line 38 of file MPIMin.c.

 {
 #ifdef serial
   int i;
   for (i = 0; i < size; i++)  global[i] = var[i];
 #else
   MPI_Allreduce((var==global?MPI_IN_PLACE:var),global,size,MPI_DOUBLE,MPI_MIN,*((MPI_Comm*)comm));
 #endif
   return(0);
 }

int MPISum_double	(	double *	global,
		double *	var,
		int	size,
		void *	comm
	)

Calculate the sum of an array of doubles over all ranks

Compute the global sum over all MPI ranks in a given communicator for double datatype.

If var is an array of size greater than 1, global will be an array of the same size with each element as the sum of that element in var on all the MPI ranks in the given communicator.

Parameters

global	array to contain the global sums
var	the local array
size	size of the local array
comm	MPI communicator

Definition at line 39 of file MPISum.c.

 {
 #ifdef serial
   int i;
   for (i = 0; i < size; i++)  global[i] = var[i];
 #else
   MPI_Allreduce((var==global?MPI_IN_PLACE:var),global,size,MPI_DOUBLE,MPI_SUM,*((MPI_Comm*)comm));
 #endif
   return(0);
 }

int MPISum_integer	(	int *	global,
		int *	var,
		int	size,
		void *	comm
	)

Calculate the sum of an array of integers over all ranks

Compute the global sum over all MPI ranks in a given communicator for int datatype.

If var is an array of size greater than 1, global will be an array of the same size with each element as the sum of that element in var on all the MPI ranks in the given communicator.

Parameters

global	array to contain the global sums
var	the local array
size	size of the local array
comm	MPI communicator

Definition at line 16 of file MPISum.c.

 {
 #ifdef serial
   int i;
   for (i = 0; i < size; i++)  global[i] = var[i];
 #else
   MPI_Allreduce((var==global?MPI_IN_PLACE:var),global,size,MPI_INT,MPI_SUM,*((MPI_Comm*)comm));
 #endif
   return(0);
 }

int MPIPartition1D	(	int	nglobal,
		int	nproc,
		int	rank
	)

Partition (along a dimension) the domain given global size and number of ranks

Given a 1D array of a given global size nglobal, and the total number of MPI ranks nproc on which it will be partitioned, this function computes the size of the local part of the 1D array on rank.

Parameters

nglobal	Global size
nproc	Total number of ranks
rank	Rank

Definition at line 14 of file MPIPartition1D.c.

 {
   int nlocal;
   if (nglobal%nproc == 0) nlocal = nglobal/nproc;
   else {
     if (rank == nproc-1)  nlocal = nglobal/nproc + nglobal%nproc;
     else                  nlocal = nglobal/nproc;
   }
   return(nlocal);
 }

int MPIRank1D	(	int	ndims,
		int *	iproc,
		int *	ip
	)

Calculate 1D rank from the n-dimensional rank

This function returns the 1D rank, given the n-dimensional rank and the total number of MPI ranks along each spatial dimension.

1D Rank: This is the rank of the process in the communicator.
n-Dimensional Rank: This represents an integer array, where each element is the rank of the process along a spatial dimension.

Consider a 2D simulation running with 21 MPI ranks - 7 along the x direction, and 3 along the y direction, as shown in the following figure:

The boldface number in the parentheses is the n-dimensional rank (n=2), while the number below it in normal typeface is the 1D rank, corresponding to the rank in the MPI communicator.

Parameters

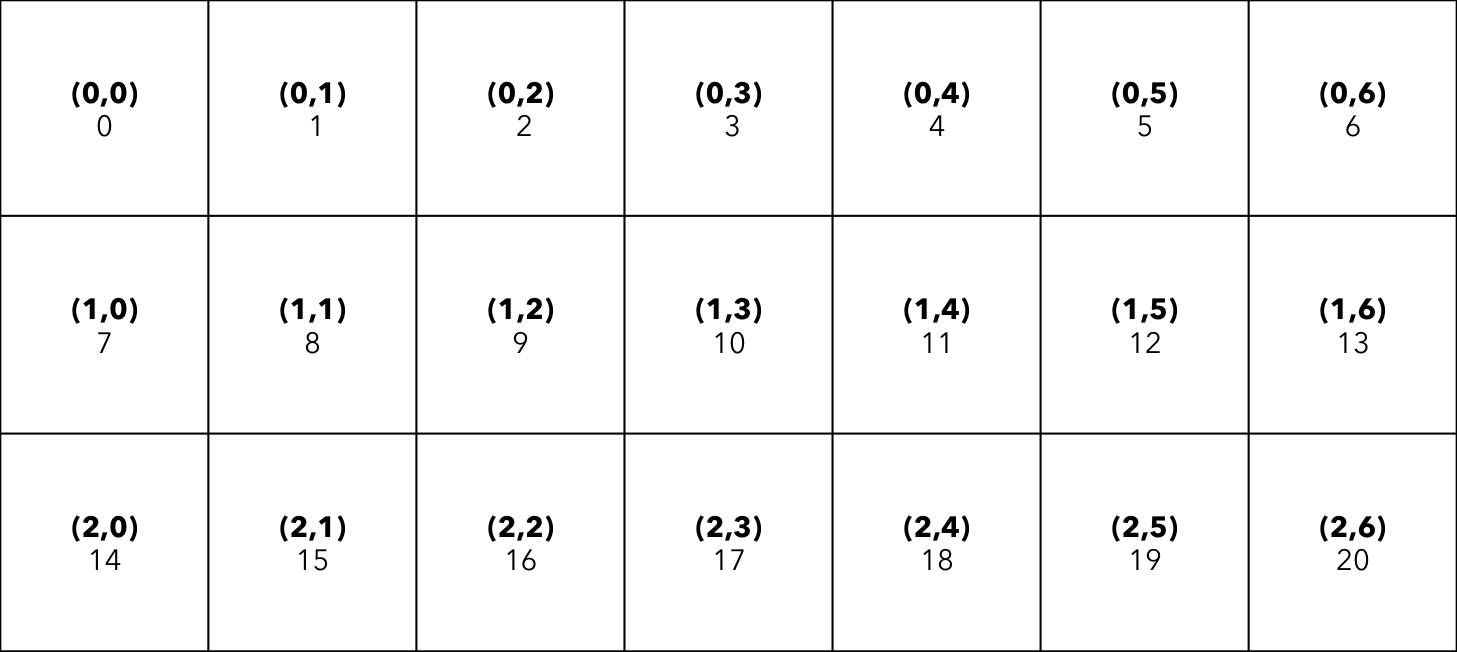
ndims	Number of spatial dimensions
iproc	Integer array whose elements are the number of MPI ranks along each dimension
ip	Integer array whose elements are the rank of this process along each dimension

Definition at line 26 of file MPIRank1D.c.

 {
   int i,rank = 0, term = 1;
   for (i=0; i<ndims; i++) {
     rank += (ip[i]*term);
     term *= iproc[i];
   }
   
   return(rank);
 }

int MPIRanknD	(	int	ndims,
		int	rank,
		int *	iproc,
		int *	ip
	)

Calculate the n-dimensional rank from the 1D rank

This function computes the n-dimensional rank, given the 1D rank and the total number of MPI ranks along each spatial dimension.

1D Rank: This is the rank of the process in the communicator.
n-Dimensional Rank: This represents an integer array, where each element is the rank of the process along a spatial dimension.

Consider a 2D simulation running with 21 MPI ranks - 7 along the x direction, and 3 along the y direction, as shown in the following figure:

The boldface number in the parentheses is the n-dimensional rank (n=2), while the number below it in normal typeface is the 1D rank, corresponding to the rank in the MPI communicator.

Note:

the array to hold the computed n-dimensional rank must be preallocated and the size must be equal to the number of spatial dimensions.

Parameters

ndims	Number of spatial dimensions
rank	1D rank
iproc	Integer array whose elements are the number of MPI ranks along each dimension
ip	Integer array whose elements are the rank of this process along each dimesion

Definition at line 27 of file MPIRanknD.c.

 {
   int i,term    = 1;
   for (i=0; i<ndims; i++) term *= iproc[i];
   for (i=ndims-1; i>=0; i--) {
     term /= iproc[i];
     ip[i] = rank/term;
     rank -= ip[i]*term;
   }
   return(0);
 }

void MPIGetFilename	(	char *	root,
		void *	c,
		char *	filename
	)

Generate a unique filename given the rank of the process to let that process write to its own file

Get a string representing a filename indexed by the MPI rank: filename = root.index, where index is the string corresponding to the MPI rank.

Parameters

root	filename root
c	MPI communicator
filename	filename

Definition at line 19 of file MPIGetFilename.c.

 {
   char  tail[_MAX_STRING_SIZE_]="";
   int   rank;
 
 #ifndef serial
   MPI_Comm  comm = *((MPI_Comm*)c);
   MPI_Comm_rank(comm,&rank);
 #else
   rank = 0;
 #endif
 
   GetStringFromInteger(rank,tail,4);
   strcpy(filename,"");
   strcat(filename,root);
   strcat(filename,"." );
   strcat(filename,tail);
 
   return;
 }

Functions

Detailed Description

Function Documentation