MPIExchangeBoundariesnD.c File Reference

Exchange data and fill in ghost points for an n-dimensional array. More...

#include <stdlib.h>
#include <basic.h>
#include <arrayfunctions.h>
#include <mpivars.h>

Go to the source code of this file.

Functions
int	MPIExchangeBoundariesnD (int ndims, int nvars, int *dim, int ghosts, void *m, double *var)

Detailed Description

Exchange data and fill in ghost points for an n-dimensional array.

Author

Debojyoti Ghosh

Definition in file MPIExchangeBoundariesnD.c.

Function Documentation

int MPIExchangeBoundariesnD	(	int	ndims,
		int	nvars,
		int *	dim,
		int	ghosts,
		void *	m,
		double *	var
	)

Exchange data across MPI ranks, and fill in ghost points for an n-dimensional array (where n is the total number of spatial dimensions). If any of the physical boundaries are periodic, this function also exchanges data and fills in the ghost points for these boundaries.

The n-dimensional array must be stored in the memory as a single-index array, with the following order of mapping:

• Number of variables (vector components)
• Spatial dimension 0
• Spatial dimension 1
• ...
• Spatial dimensions ndims-1

For example, consider a 2D simulation (ndims = 2), of size \(7 \times 3\), with \(4\) vector components (nvars = 4). The following figure shows the layout (without the ghost points):

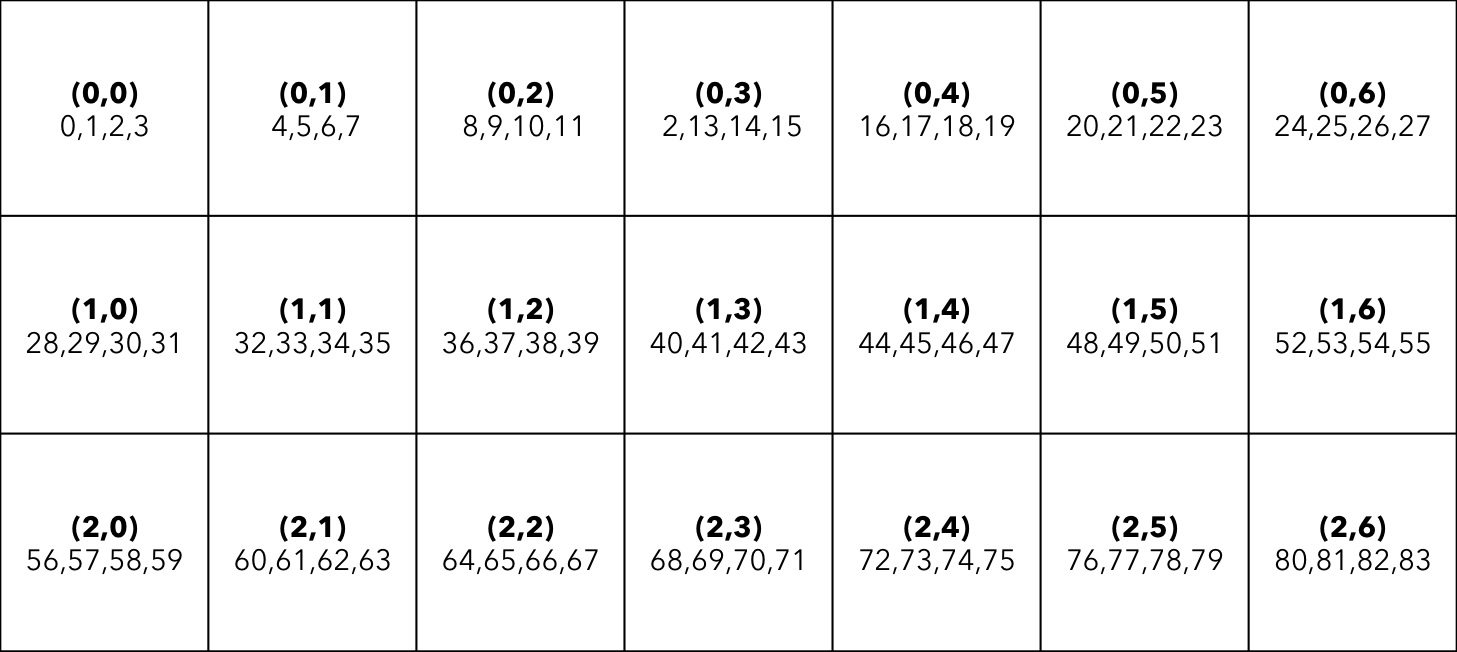
The bold numbers in parentheses represent the 2D indices. The numbers below them are the indices of the array that correspond to that 2D location. Thus, elements 40,41,42, and 43 in the array are the 1st, 2nd, 3rd, and 4th vector components at location (1,3).

If \({\bf i}\left[{\rm ndims}\right]\) is an integer array representing an n-dimensional index (for example, \(\left(5,4\right)\) in 2D, \(\left(3,5,2\right)\) in 3D), and the number of vector components is nvars, then:

• _ArrayIndex1D_ computes the index \(p\) in the array corresponding to \({\bf i}\). In the above example, \({\bf i} = \left(1,3\right) \rightarrow p = 10\).
• var[nvars*p+v] accesses the v-th component of the n-dimensional array var at location \({\bf i}\). In the above example, to access the 3rd vector component at location \(\left(1,3\right)\), we have \(p=10\), so var [4*10+2] = var [42].

Parameters

ndims	Number of spatial dimensions
nvars	Number of variables (vector components) at each grid location
dim	Integer array whose elements are the local size along each spatial dimension
ghosts	Number of ghost points
m	MPI object of type MPIVariables
var	The array for which to exchange data and fill in ghost points

Definition at line 42 of file MPIExchangeBoundariesnD.c.

{
#ifndef serial
  MPIVariables  *mpi = (MPIVariables*) m;
  int           d;
  
  int *ip     = mpi->ip;
  int *iproc  = mpi->iproc;
  int *bcflag = mpi->bcperiodic;

  int neighbor_rank[2*ndims], nip[ndims], index[ndims], bounds[ndims], offset[ndims];
  MPI_Request rcvreq[2*ndims], sndreq[2*ndims];
  for (d=0; d<2*ndims; d++) rcvreq[d] = sndreq[d] = MPI_REQUEST_NULL;

  /* each process has 2*ndims neighbors (except at non-periodic physical boundaries)  */
  /* calculate the rank of these neighbors (-1 -> none)                               */
  for (d = 0; d < ndims; d++) {
    _ArrayCopy1D_(ip,nip,ndims); 
    if (ip[d] == 0) nip[d] = iproc[d]-1;
    else            nip[d]--;
    if ((ip[d] == 0) && (!bcflag[d])) neighbor_rank[2*d]   = -1;
    else                              neighbor_rank[2*d]   = MPIRank1D(ndims,iproc,nip);
    _ArrayCopy1D_(ip,nip,ndims); 
    if (ip[d] == (iproc[d]-1)) nip[d] = 0;
    else                       nip[d]++;
    if ((ip[d] == (iproc[d]-1)) && (!bcflag[d]))  neighbor_rank[2*d+1] = -1;
    else                                          neighbor_rank[2*d+1] = MPIRank1D(ndims,iproc,nip);
  }

  /* calculate dimensions of each of the send-receive regions */
  double *sendbuf = mpi->sendbuf;
  double *recvbuf = mpi->recvbuf;
  int    stride   = mpi->maxbuf;
  int    bufdim[ndims];
  for (d = 0; d < ndims; d++) {
    bufdim[d] = 1;
    int i;
    for (i = 0; i < ndims; i++) {
      if (i == d) bufdim[d] *= ghosts;
      else        bufdim[d] *= dim[i];
    }
  }

  /* post the receive requests */
  for (d = 0; d < ndims; d++) {
    if (neighbor_rank[2*d  ] != -1) {
      MPI_Irecv(&recvbuf[2*d*stride],bufdim[d]*nvars,MPI_DOUBLE,neighbor_rank[2*d  ],1630,
                mpi->world,&rcvreq[2*d]);
    }
    if (neighbor_rank[2*d+1] != -1) {
      MPI_Irecv(&recvbuf[(2*d+1)*stride],bufdim[d]*nvars,MPI_DOUBLE,neighbor_rank[2*d+1],1631,
                mpi->world,&rcvreq[2*d+1]);
    }
  }

  /* count number of neighbors and copy data to send buffers */
  for (d = 0; d < ndims; d++) {
    _ArrayCopy1D_(dim,bounds,ndims); bounds[d] = ghosts;
    if (neighbor_rank[2*d] != -1) {
      _ArraySetValue_(offset,ndims,0);
      int done = 0; _ArraySetValue_(index,ndims,0);
      while (!done) {
        int p1; _ArrayIndex1DWO_(ndims,dim,index,offset,ghosts,p1);
        int p2; _ArrayIndex1D_(ndims,bounds,index,0,p2);
        _ArrayCopy1D_((var+nvars*p1),(sendbuf+2*d*stride+nvars*p2),nvars);
        _ArrayIncrementIndex_(ndims,bounds,index,done);
      }
    }
    if (neighbor_rank[2*d+1] != -1) {
      _ArraySetValue_(offset,ndims,0);offset[d] = dim[d]-ghosts;
      int done = 0; _ArraySetValue_(index,ndims,0);
      while (!done) {
        int p1; _ArrayIndex1DWO_(ndims,dim,index,offset,ghosts,p1);
        int p2; _ArrayIndex1D_(ndims,bounds,index,0,p2);
        _ArrayCopy1D_((var+nvars*p1),(sendbuf+(2*d+1)*stride+nvars*p2),nvars);
        _ArrayIncrementIndex_(ndims,bounds,index,done);
      }
    }
  }

  /* send the data */
  for (d = 0; d < ndims; d++) {
    if (neighbor_rank[2*d  ] != -1) {
      MPI_Isend(&sendbuf[2*d*stride],bufdim[d]*nvars,MPI_DOUBLE,neighbor_rank[2*d  ],1631,
                mpi->world,&sndreq[2*d]);
    }
    if (neighbor_rank[2*d+1] != -1) {
      MPI_Isend(&sendbuf[(2*d+1)*stride],bufdim[d]*nvars,MPI_DOUBLE,neighbor_rank[2*d+1],1630,
                mpi->world,&sndreq[2*d+1]);
    }
  }

  /* Wait till data is done received */
  MPI_Status status_arr[2*ndims];
  MPI_Waitall(2*ndims,rcvreq,status_arr);
  /* copy received data to ghost points */
  for (d = 0; d < ndims; d++) {
    _ArrayCopy1D_(dim,bounds,ndims); bounds[d] = ghosts;
    if (neighbor_rank[2*d] != -1) {
      _ArraySetValue_(offset,ndims,0); offset[d] = -ghosts;
      int done = 0; _ArraySetValue_(index,ndims,0);
      while (!done) {
        int p1; _ArrayIndex1DWO_(ndims,dim,index,offset,ghosts,p1);
        int p2; _ArrayIndex1D_(ndims,bounds,index,0,p2);
        _ArrayCopy1D_((recvbuf+2*d*stride+nvars*p2),(var+nvars*p1),nvars);
        _ArrayIncrementIndex_(ndims,bounds,index,done);
      }
    }
    if (neighbor_rank[2*d+1] != -1) {
      _ArraySetValue_(offset,ndims,0); offset[d] = dim[d];
      int done = 0; _ArraySetValue_(index,ndims,0);
      while (!done) {
        int p1; _ArrayIndex1DWO_(ndims,dim,index,offset,ghosts,p1);
        int p2; _ArrayIndex1D_(ndims,bounds,index,0,p2);
        _ArrayCopy1D_((recvbuf+(2*d+1)*stride+nvars*p2),(var+nvars*p1),nvars);
        _ArrayIncrementIndex_(ndims,bounds,index,done);
      }
    }
  }
  /* Wait till send requests are complete before freeing memory */
  MPI_Waitall(2*ndims,sndreq,status_arr);

#endif
  return(0);
}