2D Navier-Stokes Equations - Lid-Driven Square Cavity
Location: hypar/Examples/2D/NavierStokes2D/LidDrivenCavity_PETSc_IMEX (This directory contains all the input files needed to run this case. If there is a Run.m, run it in MATLAB to quickly set up, run, and visualize the example).
Governing equations: 2D Navier-Stokes Equations (navierstokes2d.h)
Reference:
- Erturk, E., Corke, T.C., and Gokcol, C., "Numerical Solutions of 2-D Steady Incompressible Driven Cavity Flow at High Reynolds Numbers", International Journal for Numerical Methods in Fluids, 48, 2005, http://dx.doi.org/10.1002/fld.953.
- Ghia, U., Ghia, K.N., Shin, C.T., "High-Re Solutions for Incompressible Flow using the Navier-Stokes Equations and a Multigrid Method", Journal of Computational Physics, 48, 1982, http://dx.doi.org/10.1016/0021-9991(82)90058-4.
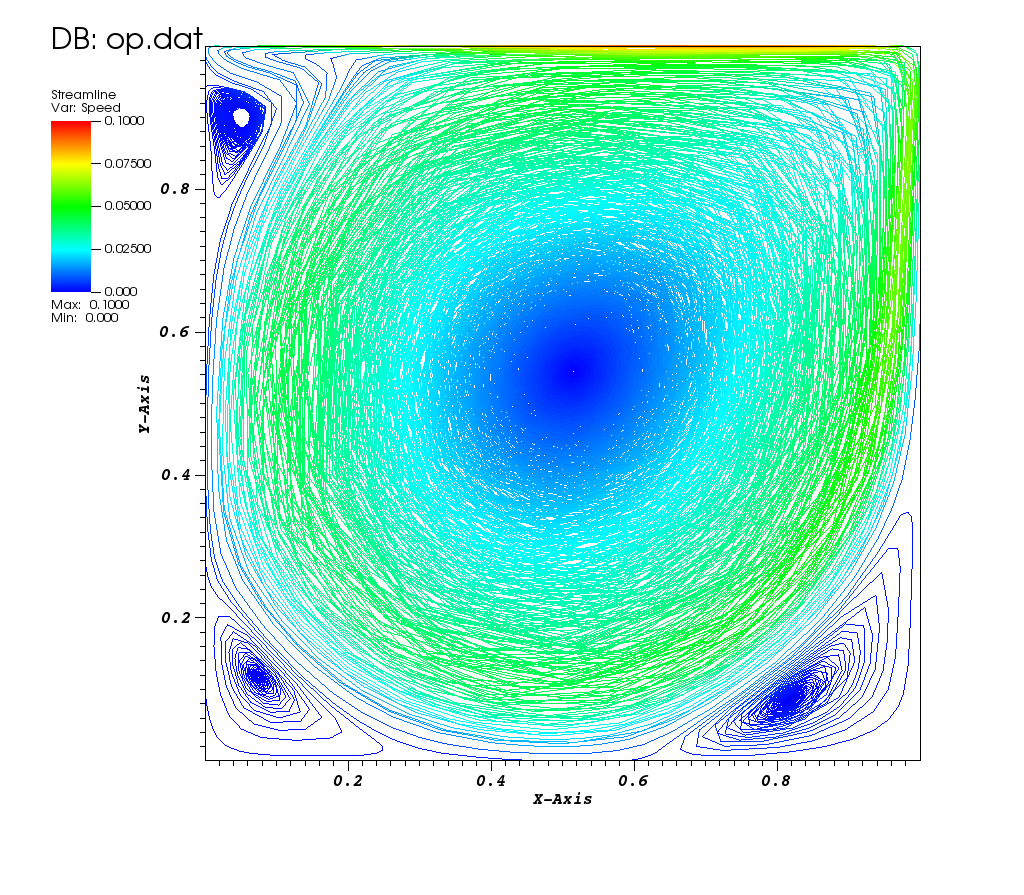
Note that this is an incompressible problem being solved here using the compressible Navier-Stokes equations in terms of non-dimensional flow variables. The density and pressure are taken such that the speed of sound is 1.0, and the flow velocities specified in the initial and boundary conditions correspond to a characteristic Mach number of 0.1 (thus, they are 0.1 times the values in the above reference).
The problem is solved here using implicit-explicit (IMEX) time integration, where the hyperbolic flux is partitioned into its entropy and acoustic components with the former integrated explicitly and the latter integrated implicitly. See:
- Ghosh, D., Constantinescu, E. M., "Semi-Implicit Time Integration of Atmospheric Flows with Characteristic-Based Flux Partitioning", SIAM Journal on Scientific Computing, 38 (3), 2016, A1848-A1875, http://dx.doi.org/10.1137/15M1044369.
Domain: \(0 \le x, y \le 1\)
Boundary conditions:
- No-slip wall BC on \(x=0,1, 0 \le y \le 1\) (_NOSLIP_WALL_ with 0 wall velocity).
- No-slip wall BC on \(y=0, 0 \le x \le 1\) (_NOSLIP_WALL_ with 0 wall velocity).
- Moving no-slip wall BC on \(y=1, 0 \le x \le 1\) (_NOSLIP_WALL_ with specified wall velocity of 0.1 in the x-direction).
Initial solution: \(\rho=1, p=1/\gamma\). The velocities are specified according to the references above, but scaled by a factor of 0.1 to ensure that the characteristic Mach number is 0.1.
Other parameters:
- \(\gamma = 1.4\) (NavierStokes2D::gamma)
- \(Re = \frac {\rho u L } {\mu} = 3200\) (Reynolds number) (NavierStokes2D::Re), where \(L=1\) is the cavity length and width.
- \(Pr = 0.72\) (Prandtl number) (NavierStokes2D::Pr)
- \(M_\infty = 0.1\) (characteristic Mach number) (NavierStokes2D::Minf)
Note: Pressure is taken as \(1/\gamma\) in the above so that the freestream speed of sound is 1.
Numerical method:
- Spatial discretization (hyperbolic): 5th order upwind (Interp1PrimFifthOrderUpwind())
- Spatial discretization (parabolic) : 4th order (FirstDerivativeFourthOrderCentral()) non-conservative 2-stage (ParabolicFunctionNC2Stage())
- Time integration: PETSc (SolvePETSc())
- Method Class: Additive Runge-Kutta method (TSARKIMEX - https://petsc.org/release/docs/manualpages/TS/TSARKIMEX.html)
- Specific method: Kennedy-Carpenter ARK4 (TSARKIMEX4 - https://petsc.org/release/docs/manualpages/TS/TSARKIMEX4.html)
Input files required:
.petscrc
# See PETSc documentation for more details (https://petsc.org/release/overview/).
# Note that if the following are specified in this file, the corresponding inputs in solver.inp are *ignored*.
# + "-ts_dt" (time step size): ignores "dt" in solver.inp
# + "-ts_max_steps" (maximum number of time iterations): ignores "n_iter" in solver.inp
# + "-ts_max_time" (final simulation time): ignores "n_iter" X "dt" in solver.inp
# Use PETSc time-integration
-use-petscts
# Time integration scheme type - ARK
-ts_type arkimex
-ts_arkimex_type 4
# Specify the terms to treat explicitly and implicitly
# In this example, the hyperbolic flux is partitioned
# into its entropy and acoustic components: f = [f-df] + [df]
# [f-df] - entropy component
# [df] - acoustic component
-hyperbolic_f_explicit # treat [f-df] explicitly
-hyperbolic_df_implicit # treat [df] implicitly
-parabolic_explicit # treat the parabolic term explicitly
# thus, time step size is limited by the [f-df] term, i.e.,
# the flow velocity.
# For linear problens, tell nonlinear solver (SNES) to only use the linear solver (KSP)
-snes_type ksponly
# Linear solver (KSP) type
-ksp_type gmres
# Set relative tolerance
-ksp_rtol 1e-6
# Set absolute tolerance
-ksp_atol 1e-12
# use a preconditioner for solving the system
-with_pc
# apply right preconditioner
-ksp_pc_side RIGHT
# preconditioner type - SOR
-pc_type sor
-pc_sor_omega 1.0
-pc_sor_its 1
solver.inp
begin
ndims 2
nvars 4
size 128 128
iproc 2 2
ghost 3
n_iter 2500
time_scheme rk
time_scheme_type 44
hyp_space_scheme upw5
hyp_flux_split yes
hyp_interp_type components
par_space_type nonconservative-2stage
par_space_scheme 4
dt 0.1
screen_op_iter 10
file_op_iter 500
input_mode serial
ip_file_type binary
output_mode serial
op_file_format tecplot2d
op_overwrite yes
model navierstokes2d
end
boundary.inp
4
noslip-wall 0 1 0 0 0 1.0
0.0 0.0
noslip-wall 0 -1 0 0 0 1.0
0.0 0.0
noslip-wall 1 1 0 1.0 0 0
0.0 0.0
noslip-wall 1 -1 0 1.0 0 0
0.1 0.0
physics.inp (Note: this file specifies \(Re = 3200\), change Re here for other Reynolds numbers.)
begin
gamma 1.4
upwinding roe
Pr 0.72
Minf 0.1
Re 3200
end
To generate initial.inp (initial solution), compile and run the following code in the run directory.
#include <stdio.h>
#include <stdlib.h>
#include <math.h>
#include <string.h>
int main()
{
double gamma = 1.4;
int NI,NJ,ndims;
char ip_file_type[50]; strcpy(ip_file_type,"ascii");
FILE *in;
printf("Reading file \"solver.inp\"...\n");
in = fopen("solver.inp","r");
if (!in) {
printf("Error: Input file \"solver.inp\" not found. Default values will be used.\n");
return(0);
} else {
char word[500];
fscanf(in,"%s",word);
if (!strcmp(word, "begin")) {
while (strcmp(word, "end")) {
fscanf(in,"%s",word);
if (!strcmp(word, "ndims")) fscanf(in,"%d",&ndims);
else if (!strcmp(word, "size")) {
fscanf(in,"%d",&NI);
fscanf(in,"%d",&NJ);
} else if (!strcmp(word, "ip_file_type")) fscanf(in,"%s",ip_file_type);
}
} else printf("Error: Illegal format in solver.inp. Crash and burn!\n");
}
fclose(in);
if (ndims != 2) {
printf("ndims is not 2 in solver.inp. this code is to generate 2D initial conditions\n");
return(0);
}
printf("Grid:\t\t\t%d X %d\n",NI,NJ);
int i,j;
double dx = 1.0 / ((double)NI-1);
double dy = 1.0 / ((double)NJ-1);
double Minf = 0.1;
double *x, *y, *u0, *u1, *u2, *u3;
x = (double*) calloc (NI , sizeof(double));
y = (double*) calloc (NJ , sizeof(double));
u0 = (double*) calloc (NI*NJ, sizeof(double));
u1 = (double*) calloc (NI*NJ, sizeof(double));
u2 = (double*) calloc (NI*NJ, sizeof(double));
u3 = (double*) calloc (NI*NJ, sizeof(double));
for (i = 0; i < NI; i++){
for (j = 0; j < NJ; j++){
x[i] = i*dx;
y[j] = j*dy;
int p = NJ*i + j;
double rho, u, v, P;
rho = 1.0;
P = 1.0/gamma;
u = Minf * (y[j]-0.5);
v = - Minf * (x[i]-0.5);
u0[p] = rho;
u1[p] = rho*u;
u2[p] = rho*v;
u3[p] = P/(gamma-1.0) + 0.5*rho*(u*u+v*v);
}
}
FILE *out;
if (!strcmp(ip_file_type,"ascii")) {
printf("Writing ASCII initial solution file initial.inp\n");
out = fopen("initial.inp","w");
for (i = 0; i < NI; i++) fprintf(out,"%lf ",x[i]);
fprintf(out,"\n");
for (j = 0; j < NJ; j++) fprintf(out,"%lf ",y[j]);
fprintf(out,"\n");
for (j = 0; j < NJ; j++) {
for (i = 0; i < NI; i++) {
int p = NJ*i + j;
fprintf(out,"%lf ",u0[p]);
}
}
fprintf(out,"\n");
for (j = 0; j < NJ; j++) {
for (i = 0; i < NI; i++) {
int p = NJ*i + j;
fprintf(out,"%lf ",u1[p]);
}
}
fprintf(out,"\n");
for (j = 0; j < NJ; j++) {
for (i = 0; i < NI; i++) {
int p = NJ*i + j;
fprintf(out,"%lf ",u2[p]);
}
}
fprintf(out,"\n");
for (j = 0; j < NJ; j++) {
for (i = 0; i < NI; i++) {
int p = NJ*i + j;
fprintf(out,"%lf ",u3[p]);
}
}
fprintf(out,"\n");
fclose(out);
} else if ((!strcmp(ip_file_type,"binary")) || (!strcmp(ip_file_type,"bin"))) {
printf("Writing binary initial solution file initial.inp\n");
out = fopen("initial.inp","wb");
fwrite(x,sizeof(double),NI,out);
fwrite(y,sizeof(double),NJ,out);
double *U = (double*) calloc (4*NI*NJ,sizeof(double));
for (i=0; i < NI; i++) {
for (j = 0; j < NJ; j++) {
int p = NJ*i + j;
int q = NI*j + i;
U[4*q+0] = u0[p];
U[4*q+1] = u1[p];
U[4*q+2] = u2[p];
U[4*q+3] = u3[p];
}
}
fwrite(U,sizeof(double),4*NI*NJ,out);
free(U);
fclose(out);
}
free(x);
free(y);
free(u0);
free(u1);
free(u2);
free(u3);
return(0);
}
Output:
Note that iproc is set to
2 2
in solver.inp (i.e., 2 processors along x, and 2 processor along y). Thus, this example should be run with 4 MPI ranks (or change iproc).
After running the code, there should be one output file op.dat, since HyPar::op_overwrite is set to yes in solver.inp. Since HyPar::op_file_format is set to tecplot2d in solver.inp, this file is in the ASCII Tecplot format and can be viewed in any software that supports this format (e.g. VisIt).
The following plot shows the streamlines (colored by the velocity magnitude):
The file function_counts.dat reports the computational expense (in terms of the number of function counts):
2500
312343
15000
297343
15000
27500
12500
269843
The numbers are, respectively,
- Time iterations
- Number of times the hyperbolic term was evaluated
- Number of times the parabolic term was evaluated
- Number of times the source term was evaluated
- Number of calls to the explicit right-hand-side function (PetscRHSFunctionIMEX() or PetscRHSFunctionExpl())
- Number of calls to the implicit right-hand-side function (PetscIFunctionIMEX() or PetscRHSFunctionImpl())
- Number of calls to the Jacobian (PetscIJacobianIMEX() or PetscIJacobian())
- Number of calls to the matrix-free Jacobian function (PetscJacobianFunctionIMEX_Linear(), PetscJacobianFunctionIMEX_JFNK(), PetscJacobianFunction_JFNK(), or PetscJacobianFunction_Linear()).
Expected screen output (for Reynolds number 3200):
HyPar - Parallel (MPI) version with 4 processes
Compiled with PETSc time integration.
Reading solver inputs from file "solver.inp".
No. of dimensions : 2
No. of variables : 4
Domain size : 128 128
Processes along each dimension : 2 2
No. of ghosts pts : 3
No. of iter. : 2500
Restart iteration : 0
Time integration scheme : PETSc
Spatial discretization scheme (hyperbolic) : upw5
Split hyperbolic flux term? : yes
Interpolation type for hyperbolic term : components
Spatial discretization type (parabolic ) : nonconservative-2stage
Spatial discretization scheme (parabolic ) : 4
Time Step : 1.000000E-01
Check for conservation : no
Screen output iterations : 10
File output iterations : 500
Initial solution file type : binary
Initial solution read mode : serial
Solution file write mode : serial
Solution file format : tecplot2d
Overwrite solution file : yes
Physical model : navierstokes2d
Partitioning domain.
Allocating data arrays.
Reading array from binary file initial.inp (Serial mode).
Volume integral of the initial solution:
0: 1.0158100316201648E+00
1: 3.8857805861880479E-16
2: 2.6020852139652106E-18
3: 1.8148063242358221E+00
Reading boundary conditions from "boundary.inp".
Boundary noslip-wall: Along dimension 0 and face +1
Boundary noslip-wall: Along dimension 0 and face -1
Boundary noslip-wall: Along dimension 1 and face +1
Boundary noslip-wall: Along dimension 1 and face -1
4 boundary condition(s) read.
Initializing solvers.
Initializing physics. Model = "navierstokes2d"
Reading physical model inputs from file "physics.inp".
Setting up PETSc time integration...
PETSc: total number of computational points is 16384.
Implicit-Explicit time-integration:-
Hyperbolic (f-df) term: Explicit
Hyperbolic (df) term: Implicit
Parabolic term: Explicit
Source term: Implicit
SolvePETSc(): Problem type is linear.
** Starting PETSc time integration **
Writing solution file op.dat.
Iteration: 10 Time: 1.000E+00 Max CFL: 1.392E+01 Max Diff. No.: -1.000E+00 Norm: 4.3681E-02
Iteration: 20 Time: 2.000E+00 Max CFL: 1.384E+01 Max Diff. No.: -1.000E+00 Norm: 4.1713E-02
Iteration: 30 Time: 3.000E+00 Max CFL: 1.406E+01 Max Diff. No.: -1.000E+00 Norm: 3.4458E-02
Iteration: 40 Time: 4.000E+00 Max CFL: 1.395E+01 Max Diff. No.: -1.000E+00 Norm: 3.6000E-02
Iteration: 50 Time: 5.000E+00 Max CFL: 1.405E+01 Max Diff. No.: -1.000E+00 Norm: 3.6129E-02
Iteration: 60 Time: 6.000E+00 Max CFL: 1.424E+01 Max Diff. No.: -1.000E+00 Norm: 3.6452E-02
Iteration: 70 Time: 7.000E+00 Max CFL: 1.402E+01 Max Diff. No.: -1.000E+00 Norm: 3.8710E-02
Iteration: 80 Time: 8.000E+00 Max CFL: 1.417E+01 Max Diff. No.: -1.000E+00 Norm: 3.8551E-02
Iteration: 90 Time: 9.000E+00 Max CFL: 1.404E+01 Max Diff. No.: -1.000E+00 Norm: 3.4447E-02
Iteration: 100 Time: 1.000E+01 Max CFL: 1.407E+01 Max Diff. No.: -1.000E+00 Norm: 3.0761E-02
Iteration: 110 Time: 1.100E+01 Max CFL: 1.406E+01 Max Diff. No.: -1.000E+00 Norm: 2.6699E-02
Iteration: 120 Time: 1.200E+01 Max CFL: 1.395E+01 Max Diff. No.: -1.000E+00 Norm: 2.2372E-02
Iteration: 130 Time: 1.300E+01 Max CFL: 1.410E+01 Max Diff. No.: -1.000E+00 Norm: 2.5665E-02
Iteration: 140 Time: 1.400E+01 Max CFL: 1.394E+01 Max Diff. No.: -1.000E+00 Norm: 2.8161E-02
Iteration: 150 Time: 1.500E+01 Max CFL: 1.409E+01 Max Diff. No.: -1.000E+00 Norm: 2.7861E-02
Iteration: 160 Time: 1.600E+01 Max CFL: 1.388E+01 Max Diff. No.: -1.000E+00 Norm: 2.6930E-02
Iteration: 170 Time: 1.700E+01 Max CFL: 1.398E+01 Max Diff. No.: -1.000E+00 Norm: 2.4366E-02
Iteration: 180 Time: 1.800E+01 Max CFL: 1.393E+01 Max Diff. No.: -1.000E+00 Norm: 1.9179E-02
Iteration: 190 Time: 1.900E+01 Max CFL: 1.404E+01 Max Diff. No.: -1.000E+00 Norm: 1.7873E-02
Iteration: 200 Time: 2.000E+01 Max CFL: 1.404E+01 Max Diff. No.: -1.000E+00 Norm: 2.0336E-02
Iteration: 210 Time: 2.100E+01 Max CFL: 1.398E+01 Max Diff. No.: -1.000E+00 Norm: 2.1216E-02
Iteration: 220 Time: 2.200E+01 Max CFL: 1.407E+01 Max Diff. No.: -1.000E+00 Norm: 2.2265E-02
Iteration: 230 Time: 2.300E+01 Max CFL: 1.389E+01 Max Diff. No.: -1.000E+00 Norm: 2.0843E-02
Iteration: 240 Time: 2.400E+01 Max CFL: 1.402E+01 Max Diff. No.: -1.000E+00 Norm: 1.8235E-02
Iteration: 250 Time: 2.500E+01 Max CFL: 1.402E+01 Max Diff. No.: -1.000E+00 Norm: 1.6319E-02
Iteration: 260 Time: 2.600E+01 Max CFL: 1.401E+01 Max Diff. No.: -1.000E+00 Norm: 1.8137E-02
Iteration: 270 Time: 2.700E+01 Max CFL: 1.411E+01 Max Diff. No.: -1.000E+00 Norm: 1.9702E-02
Iteration: 280 Time: 2.800E+01 Max CFL: 1.398E+01 Max Diff. No.: -1.000E+00 Norm: 2.2773E-02
Iteration: 290 Time: 2.900E+01 Max CFL: 1.405E+01 Max Diff. No.: -1.000E+00 Norm: 2.3578E-02
Iteration: 300 Time: 3.000E+01 Max CFL: 1.391E+01 Max Diff. No.: -1.000E+00 Norm: 2.1728E-02
Iteration: 310 Time: 3.100E+01 Max CFL: 1.397E+01 Max Diff. No.: -1.000E+00 Norm: 1.9399E-02
Iteration: 320 Time: 3.200E+01 Max CFL: 1.391E+01 Max Diff. No.: -1.000E+00 Norm: 1.6707E-02
Iteration: 330 Time: 3.300E+01 Max CFL: 1.390E+01 Max Diff. No.: -1.000E+00 Norm: 1.5621E-02
Iteration: 340 Time: 3.400E+01 Max CFL: 1.399E+01 Max Diff. No.: -1.000E+00 Norm: 1.7142E-02
Iteration: 350 Time: 3.500E+01 Max CFL: 1.387E+01 Max Diff. No.: -1.000E+00 Norm: 1.9605E-02
Iteration: 360 Time: 3.600E+01 Max CFL: 1.399E+01 Max Diff. No.: -1.000E+00 Norm: 2.0259E-02
Iteration: 370 Time: 3.700E+01 Max CFL: 1.384E+01 Max Diff. No.: -1.000E+00 Norm: 1.9054E-02
Iteration: 380 Time: 3.800E+01 Max CFL: 1.392E+01 Max Diff. No.: -1.000E+00 Norm: 1.6559E-02
Iteration: 390 Time: 3.900E+01 Max CFL: 1.393E+01 Max Diff. No.: -1.000E+00 Norm: 1.3437E-02
Iteration: 400 Time: 4.000E+01 Max CFL: 1.394E+01 Max Diff. No.: -1.000E+00 Norm: 1.2596E-02
Iteration: 410 Time: 4.100E+01 Max CFL: 1.399E+01 Max Diff. No.: -1.000E+00 Norm: 1.3553E-02
Iteration: 420 Time: 4.200E+01 Max CFL: 1.391E+01 Max Diff. No.: -1.000E+00 Norm: 1.4767E-02
Iteration: 430 Time: 4.300E+01 Max CFL: 1.399E+01 Max Diff. No.: -1.000E+00 Norm: 1.5438E-02
Iteration: 440 Time: 4.400E+01 Max CFL: 1.389E+01 Max Diff. No.: -1.000E+00 Norm: 1.4229E-02
Iteration: 450 Time: 4.500E+01 Max CFL: 1.394E+01 Max Diff. No.: -1.000E+00 Norm: 1.1644E-02
Iteration: 460 Time: 4.600E+01 Max CFL: 1.391E+01 Max Diff. No.: -1.000E+00 Norm: 8.8885E-03
Iteration: 470 Time: 4.700E+01 Max CFL: 1.392E+01 Max Diff. No.: -1.000E+00 Norm: 8.8491E-03
Iteration: 480 Time: 4.800E+01 Max CFL: 1.399E+01 Max Diff. No.: -1.000E+00 Norm: 1.0500E-02
Iteration: 490 Time: 4.900E+01 Max CFL: 1.390E+01 Max Diff. No.: -1.000E+00 Norm: 1.3246E-02
Iteration: 500 Time: 5.000E+01 Max CFL: 1.400E+01 Max Diff. No.: -1.000E+00 Norm: 1.4560E-02
Writing solution file op.dat.
Iteration: 510 Time: 5.100E+01 Max CFL: 1.389E+01 Max Diff. No.: -1.000E+00 Norm: 1.4228E-02
Iteration: 520 Time: 5.200E+01 Max CFL: 1.392E+01 Max Diff. No.: -1.000E+00 Norm: 1.2261E-02
Iteration: 530 Time: 5.300E+01 Max CFL: 1.389E+01 Max Diff. No.: -1.000E+00 Norm: 1.0152E-02
Iteration: 540 Time: 5.400E+01 Max CFL: 1.389E+01 Max Diff. No.: -1.000E+00 Norm: 9.5872E-03
Iteration: 550 Time: 5.500E+01 Max CFL: 1.393E+01 Max Diff. No.: -1.000E+00 Norm: 1.1004E-02
Iteration: 560 Time: 5.600E+01 Max CFL: 1.387E+01 Max Diff. No.: -1.000E+00 Norm: 1.3115E-02
Iteration: 570 Time: 5.700E+01 Max CFL: 1.394E+01 Max Diff. No.: -1.000E+00 Norm: 1.3906E-02
Iteration: 580 Time: 5.800E+01 Max CFL: 1.383E+01 Max Diff. No.: -1.000E+00 Norm: 1.3950E-02
Iteration: 590 Time: 5.900E+01 Max CFL: 1.391E+01 Max Diff. No.: -1.000E+00 Norm: 1.2213E-02
Iteration: 600 Time: 6.000E+01 Max CFL: 1.389E+01 Max Diff. No.: -1.000E+00 Norm: 1.0714E-02
Iteration: 610 Time: 6.100E+01 Max CFL: 1.392E+01 Max Diff. No.: -1.000E+00 Norm: 9.5758E-03
Iteration: 620 Time: 6.200E+01 Max CFL: 1.392E+01 Max Diff. No.: -1.000E+00 Norm: 1.0469E-02
Iteration: 630 Time: 6.300E+01 Max CFL: 1.390E+01 Max Diff. No.: -1.000E+00 Norm: 1.1389E-02
Iteration: 640 Time: 6.400E+01 Max CFL: 1.395E+01 Max Diff. No.: -1.000E+00 Norm: 1.2203E-02
Iteration: 650 Time: 6.500E+01 Max CFL: 1.385E+01 Max Diff. No.: -1.000E+00 Norm: 1.1679E-02
Iteration: 660 Time: 6.600E+01 Max CFL: 1.394E+01 Max Diff. No.: -1.000E+00 Norm: 1.0098E-02
Iteration: 670 Time: 6.700E+01 Max CFL: 1.391E+01 Max Diff. No.: -1.000E+00 Norm: 7.8877E-03
Iteration: 680 Time: 6.800E+01 Max CFL: 1.392E+01 Max Diff. No.: -1.000E+00 Norm: 6.5575E-03
Iteration: 690 Time: 6.900E+01 Max CFL: 1.395E+01 Max Diff. No.: -1.000E+00 Norm: 7.5027E-03
Iteration: 700 Time: 7.000E+01 Max CFL: 1.388E+01 Max Diff. No.: -1.000E+00 Norm: 8.9329E-03
Iteration: 710 Time: 7.100E+01 Max CFL: 1.395E+01 Max Diff. No.: -1.000E+00 Norm: 1.0052E-02
Iteration: 720 Time: 7.200E+01 Max CFL: 1.385E+01 Max Diff. No.: -1.000E+00 Norm: 9.7624E-03
Iteration: 730 Time: 7.300E+01 Max CFL: 1.391E+01 Max Diff. No.: -1.000E+00 Norm: 8.6029E-03
Iteration: 740 Time: 7.400E+01 Max CFL: 1.388E+01 Max Diff. No.: -1.000E+00 Norm: 6.7528E-03
Iteration: 750 Time: 7.500E+01 Max CFL: 1.386E+01 Max Diff. No.: -1.000E+00 Norm: 5.7982E-03
Iteration: 760 Time: 7.600E+01 Max CFL: 1.392E+01 Max Diff. No.: -1.000E+00 Norm: 6.5512E-03
Iteration: 770 Time: 7.700E+01 Max CFL: 1.385E+01 Max Diff. No.: -1.000E+00 Norm: 7.8724E-03
Iteration: 780 Time: 7.800E+01 Max CFL: 1.392E+01 Max Diff. No.: -1.000E+00 Norm: 8.9397E-03
Iteration: 790 Time: 7.900E+01 Max CFL: 1.386E+01 Max Diff. No.: -1.000E+00 Norm: 8.9638E-03
Iteration: 800 Time: 8.000E+01 Max CFL: 1.391E+01 Max Diff. No.: -1.000E+00 Norm: 8.3957E-03
Iteration: 810 Time: 8.100E+01 Max CFL: 1.390E+01 Max Diff. No.: -1.000E+00 Norm: 7.0422E-03
Iteration: 820 Time: 8.200E+01 Max CFL: 1.389E+01 Max Diff. No.: -1.000E+00 Norm: 6.1932E-03
Iteration: 830 Time: 8.300E+01 Max CFL: 1.394E+01 Max Diff. No.: -1.000E+00 Norm: 6.5173E-03
Iteration: 840 Time: 8.400E+01 Max CFL: 1.386E+01 Max Diff. No.: -1.000E+00 Norm: 7.6061E-03
Iteration: 850 Time: 8.500E+01 Max CFL: 1.392E+01 Max Diff. No.: -1.000E+00 Norm: 8.4824E-03
Iteration: 860 Time: 8.600E+01 Max CFL: 1.385E+01 Max Diff. No.: -1.000E+00 Norm: 8.3901E-03
Iteration: 870 Time: 8.700E+01 Max CFL: 1.388E+01 Max Diff. No.: -1.000E+00 Norm: 7.6613E-03
Iteration: 880 Time: 8.800E+01 Max CFL: 1.387E+01 Max Diff. No.: -1.000E+00 Norm: 6.3115E-03
Iteration: 890 Time: 8.900E+01 Max CFL: 1.388E+01 Max Diff. No.: -1.000E+00 Norm: 5.4274E-03
Iteration: 900 Time: 9.000E+01 Max CFL: 1.391E+01 Max Diff. No.: -1.000E+00 Norm: 5.6019E-03
Iteration: 910 Time: 9.100E+01 Max CFL: 1.387E+01 Max Diff. No.: -1.000E+00 Norm: 6.4322E-03
Iteration: 920 Time: 9.200E+01 Max CFL: 1.391E+01 Max Diff. No.: -1.000E+00 Norm: 7.1296E-03
Iteration: 930 Time: 9.300E+01 Max CFL: 1.385E+01 Max Diff. No.: -1.000E+00 Norm: 7.0804E-03
Iteration: 940 Time: 9.400E+01 Max CFL: 1.388E+01 Max Diff. No.: -1.000E+00 Norm: 6.6259E-03
Iteration: 950 Time: 9.500E+01 Max CFL: 1.387E+01 Max Diff. No.: -1.000E+00 Norm: 5.5754E-03
Iteration: 960 Time: 9.600E+01 Max CFL: 1.389E+01 Max Diff. No.: -1.000E+00 Norm: 4.9023E-03
Iteration: 970 Time: 9.700E+01 Max CFL: 1.389E+01 Max Diff. No.: -1.000E+00 Norm: 4.5834E-03
Iteration: 980 Time: 9.800E+01 Max CFL: 1.385E+01 Max Diff. No.: -1.000E+00 Norm: 5.4668E-03
Iteration: 990 Time: 9.900E+01 Max CFL: 1.390E+01 Max Diff. No.: -1.000E+00 Norm: 6.0141E-03
Iteration: 1000 Time: 1.000E+02 Max CFL: 1.386E+01 Max Diff. No.: -1.000E+00 Norm: 6.3301E-03
Writing solution file op.dat.
Iteration: 1010 Time: 1.010E+02 Max CFL: 1.390E+01 Max Diff. No.: -1.000E+00 Norm: 5.7850E-03
Iteration: 1020 Time: 1.020E+02 Max CFL: 1.389E+01 Max Diff. No.: -1.000E+00 Norm: 5.1133E-03
Iteration: 1030 Time: 1.030E+02 Max CFL: 1.389E+01 Max Diff. No.: -1.000E+00 Norm: 4.4163E-03
Iteration: 1040 Time: 1.040E+02 Max CFL: 1.391E+01 Max Diff. No.: -1.000E+00 Norm: 4.4964E-03
Iteration: 1050 Time: 1.050E+02 Max CFL: 1.386E+01 Max Diff. No.: -1.000E+00 Norm: 5.0983E-03
Iteration: 1060 Time: 1.060E+02 Max CFL: 1.390E+01 Max Diff. No.: -1.000E+00 Norm: 5.5349E-03
Iteration: 1070 Time: 1.070E+02 Max CFL: 1.384E+01 Max Diff. No.: -1.000E+00 Norm: 5.6673E-03
Iteration: 1080 Time: 1.080E+02 Max CFL: 1.389E+01 Max Diff. No.: -1.000E+00 Norm: 5.1812E-03
Iteration: 1090 Time: 1.090E+02 Max CFL: 1.388E+01 Max Diff. No.: -1.000E+00 Norm: 4.6815E-03
Iteration: 1100 Time: 1.100E+02 Max CFL: 1.387E+01 Max Diff. No.: -1.000E+00 Norm: 4.1290E-03
Iteration: 1110 Time: 1.110E+02 Max CFL: 1.390E+01 Max Diff. No.: -1.000E+00 Norm: 4.0767E-03
Iteration: 1120 Time: 1.120E+02 Max CFL: 1.385E+01 Max Diff. No.: -1.000E+00 Norm: 4.3484E-03
Iteration: 1130 Time: 1.130E+02 Max CFL: 1.390E+01 Max Diff. No.: -1.000E+00 Norm: 4.6737E-03
Iteration: 1140 Time: 1.140E+02 Max CFL: 1.386E+01 Max Diff. No.: -1.000E+00 Norm: 4.8770E-03
Iteration: 1150 Time: 1.150E+02 Max CFL: 1.387E+01 Max Diff. No.: -1.000E+00 Norm: 4.5404E-03
Iteration: 1160 Time: 1.160E+02 Max CFL: 1.388E+01 Max Diff. No.: -1.000E+00 Norm: 4.1990E-03
Iteration: 1170 Time: 1.170E+02 Max CFL: 1.386E+01 Max Diff. No.: -1.000E+00 Norm: 3.6864E-03
Iteration: 1180 Time: 1.180E+02 Max CFL: 1.390E+01 Max Diff. No.: -1.000E+00 Norm: 3.7270E-03
Iteration: 1190 Time: 1.190E+02 Max CFL: 1.385E+01 Max Diff. No.: -1.000E+00 Norm: 3.9364E-03
Iteration: 1200 Time: 1.200E+02 Max CFL: 1.389E+01 Max Diff. No.: -1.000E+00 Norm: 4.2530E-03
Iteration: 1210 Time: 1.210E+02 Max CFL: 1.387E+01 Max Diff. No.: -1.000E+00 Norm: 4.3136E-03
Iteration: 1220 Time: 1.220E+02 Max CFL: 1.389E+01 Max Diff. No.: -1.000E+00 Norm: 4.0568E-03
Iteration: 1230 Time: 1.230E+02 Max CFL: 1.389E+01 Max Diff. No.: -1.000E+00 Norm: 3.7766E-03
Iteration: 1240 Time: 1.240E+02 Max CFL: 1.389E+01 Max Diff. No.: -1.000E+00 Norm: 3.5717E-03
Iteration: 1250 Time: 1.250E+02 Max CFL: 1.391E+01 Max Diff. No.: -1.000E+00 Norm: 3.7232E-03
Iteration: 1260 Time: 1.260E+02 Max CFL: 1.388E+01 Max Diff. No.: -1.000E+00 Norm: 3.8689E-03
Iteration: 1270 Time: 1.270E+02 Max CFL: 1.390E+01 Max Diff. No.: -1.000E+00 Norm: 3.9891E-03
Iteration: 1280 Time: 1.280E+02 Max CFL: 1.386E+01 Max Diff. No.: -1.000E+00 Norm: 3.9520E-03
Iteration: 1290 Time: 1.290E+02 Max CFL: 1.388E+01 Max Diff. No.: -1.000E+00 Norm: 3.7587E-03
Iteration: 1300 Time: 1.300E+02 Max CFL: 1.388E+01 Max Diff. No.: -1.000E+00 Norm: 3.5858E-03
Iteration: 1310 Time: 1.310E+02 Max CFL: 1.388E+01 Max Diff. No.: -1.000E+00 Norm: 3.3822E-03
Iteration: 1320 Time: 1.320E+02 Max CFL: 1.389E+01 Max Diff. No.: -1.000E+00 Norm: 3.4555E-03
Iteration: 1330 Time: 1.330E+02 Max CFL: 1.386E+01 Max Diff. No.: -1.000E+00 Norm: 3.4292E-03
Iteration: 1340 Time: 1.340E+02 Max CFL: 1.389E+01 Max Diff. No.: -1.000E+00 Norm: 3.5562E-03
Iteration: 1350 Time: 1.350E+02 Max CFL: 1.386E+01 Max Diff. No.: -1.000E+00 Norm: 3.3701E-03
Iteration: 1360 Time: 1.360E+02 Max CFL: 1.388E+01 Max Diff. No.: -1.000E+00 Norm: 3.2381E-03
Iteration: 1370 Time: 1.370E+02 Max CFL: 1.388E+01 Max Diff. No.: -1.000E+00 Norm: 2.9263E-03
Iteration: 1380 Time: 1.380E+02 Max CFL: 1.387E+01 Max Diff. No.: -1.000E+00 Norm: 2.9126E-03
Iteration: 1390 Time: 1.390E+02 Max CFL: 1.389E+01 Max Diff. No.: -1.000E+00 Norm: 2.9915E-03
Iteration: 1400 Time: 1.400E+02 Max CFL: 1.385E+01 Max Diff. No.: -1.000E+00 Norm: 3.1312E-03
Iteration: 1410 Time: 1.410E+02 Max CFL: 1.390E+01 Max Diff. No.: -1.000E+00 Norm: 3.0848E-03
Iteration: 1420 Time: 1.420E+02 Max CFL: 1.387E+01 Max Diff. No.: -1.000E+00 Norm: 2.8418E-03
Iteration: 1430 Time: 1.430E+02 Max CFL: 1.389E+01 Max Diff. No.: -1.000E+00 Norm: 2.6295E-03
Iteration: 1440 Time: 1.440E+02 Max CFL: 1.389E+01 Max Diff. No.: -1.000E+00 Norm: 2.4825E-03
Iteration: 1450 Time: 1.450E+02 Max CFL: 1.387E+01 Max Diff. No.: -1.000E+00 Norm: 2.6380E-03
Iteration: 1460 Time: 1.460E+02 Max CFL: 1.390E+01 Max Diff. No.: -1.000E+00 Norm: 2.7685E-03
Iteration: 1470 Time: 1.470E+02 Max CFL: 1.386E+01 Max Diff. No.: -1.000E+00 Norm: 2.8893E-03
Iteration: 1480 Time: 1.480E+02 Max CFL: 1.389E+01 Max Diff. No.: -1.000E+00 Norm: 2.8176E-03
Iteration: 1490 Time: 1.490E+02 Max CFL: 1.386E+01 Max Diff. No.: -1.000E+00 Norm: 2.6256E-03
Iteration: 1500 Time: 1.500E+02 Max CFL: 1.387E+01 Max Diff. No.: -1.000E+00 Norm: 2.4486E-03
Writing solution file op.dat.
Iteration: 1510 Time: 1.510E+02 Max CFL: 1.388E+01 Max Diff. No.: -1.000E+00 Norm: 2.2963E-03
Iteration: 1520 Time: 1.520E+02 Max CFL: 1.386E+01 Max Diff. No.: -1.000E+00 Norm: 2.4279E-03
Iteration: 1530 Time: 1.530E+02 Max CFL: 1.389E+01 Max Diff. No.: -1.000E+00 Norm: 2.5435E-03
Iteration: 1540 Time: 1.540E+02 Max CFL: 1.386E+01 Max Diff. No.: -1.000E+00 Norm: 2.7304E-03
Iteration: 1550 Time: 1.550E+02 Max CFL: 1.388E+01 Max Diff. No.: -1.000E+00 Norm: 2.6208E-03
Iteration: 1560 Time: 1.560E+02 Max CFL: 1.387E+01 Max Diff. No.: -1.000E+00 Norm: 2.3881E-03
Iteration: 1570 Time: 1.570E+02 Max CFL: 1.387E+01 Max Diff. No.: -1.000E+00 Norm: 2.0429E-03
Iteration: 1580 Time: 1.580E+02 Max CFL: 1.388E+01 Max Diff. No.: -1.000E+00 Norm: 1.9215E-03
Iteration: 1590 Time: 1.590E+02 Max CFL: 1.387E+01 Max Diff. No.: -1.000E+00 Norm: 2.1210E-03
Iteration: 1600 Time: 1.600E+02 Max CFL: 1.389E+01 Max Diff. No.: -1.000E+00 Norm: 2.3433E-03
Iteration: 1610 Time: 1.610E+02 Max CFL: 1.386E+01 Max Diff. No.: -1.000E+00 Norm: 2.5018E-03
Iteration: 1620 Time: 1.620E+02 Max CFL: 1.388E+01 Max Diff. No.: -1.000E+00 Norm: 2.3360E-03
Iteration: 1630 Time: 1.630E+02 Max CFL: 1.386E+01 Max Diff. No.: -1.000E+00 Norm: 2.0864E-03
Iteration: 1640 Time: 1.640E+02 Max CFL: 1.388E+01 Max Diff. No.: -1.000E+00 Norm: 1.7442E-03
Iteration: 1650 Time: 1.650E+02 Max CFL: 1.388E+01 Max Diff. No.: -1.000E+00 Norm: 1.6949E-03
Iteration: 1660 Time: 1.660E+02 Max CFL: 1.388E+01 Max Diff. No.: -1.000E+00 Norm: 1.8870E-03
Iteration: 1670 Time: 1.670E+02 Max CFL: 1.389E+01 Max Diff. No.: -1.000E+00 Norm: 2.1219E-03
Iteration: 1680 Time: 1.680E+02 Max CFL: 1.387E+01 Max Diff. No.: -1.000E+00 Norm: 2.2994E-03
Iteration: 1690 Time: 1.690E+02 Max CFL: 1.389E+01 Max Diff. No.: -1.000E+00 Norm: 2.2018E-03
Iteration: 1700 Time: 1.700E+02 Max CFL: 1.387E+01 Max Diff. No.: -1.000E+00 Norm: 2.0058E-03
Iteration: 1710 Time: 1.710E+02 Max CFL: 1.388E+01 Max Diff. No.: -1.000E+00 Norm: 1.6276E-03
Iteration: 1720 Time: 1.720E+02 Max CFL: 1.388E+01 Max Diff. No.: -1.000E+00 Norm: 1.5591E-03
Iteration: 1730 Time: 1.730E+02 Max CFL: 1.387E+01 Max Diff. No.: -1.000E+00 Norm: 1.6899E-03
Iteration: 1740 Time: 1.740E+02 Max CFL: 1.389E+01 Max Diff. No.: -1.000E+00 Norm: 2.0180E-03
Iteration: 1750 Time: 1.750E+02 Max CFL: 1.386E+01 Max Diff. No.: -1.000E+00 Norm: 2.1536E-03
Iteration: 1760 Time: 1.760E+02 Max CFL: 1.389E+01 Max Diff. No.: -1.000E+00 Norm: 2.0718E-03
Iteration: 1770 Time: 1.770E+02 Max CFL: 1.387E+01 Max Diff. No.: -1.000E+00 Norm: 1.7735E-03
Iteration: 1780 Time: 1.780E+02 Max CFL: 1.388E+01 Max Diff. No.: -1.000E+00 Norm: 1.3853E-03
Iteration: 1790 Time: 1.790E+02 Max CFL: 1.388E+01 Max Diff. No.: -1.000E+00 Norm: 1.2944E-03
Iteration: 1800 Time: 1.800E+02 Max CFL: 1.387E+01 Max Diff. No.: -1.000E+00 Norm: 1.4519E-03
Iteration: 1810 Time: 1.810E+02 Max CFL: 1.389E+01 Max Diff. No.: -1.000E+00 Norm: 1.7747E-03
Iteration: 1820 Time: 1.820E+02 Max CFL: 1.386E+01 Max Diff. No.: -1.000E+00 Norm: 1.8713E-03
Iteration: 1830 Time: 1.830E+02 Max CFL: 1.389E+01 Max Diff. No.: -1.000E+00 Norm: 1.8034E-03
Iteration: 1840 Time: 1.840E+02 Max CFL: 1.387E+01 Max Diff. No.: -1.000E+00 Norm: 1.5043E-03
Iteration: 1850 Time: 1.850E+02 Max CFL: 1.388E+01 Max Diff. No.: -1.000E+00 Norm: 1.1537E-03
Iteration: 1860 Time: 1.860E+02 Max CFL: 1.388E+01 Max Diff. No.: -1.000E+00 Norm: 1.0051E-03
Iteration: 1870 Time: 1.870E+02 Max CFL: 1.387E+01 Max Diff. No.: -1.000E+00 Norm: 1.1630E-03
Iteration: 1880 Time: 1.880E+02 Max CFL: 1.389E+01 Max Diff. No.: -1.000E+00 Norm: 1.5157E-03
Iteration: 1890 Time: 1.890E+02 Max CFL: 1.387E+01 Max Diff. No.: -1.000E+00 Norm: 1.6714E-03
Iteration: 1900 Time: 1.900E+02 Max CFL: 1.389E+01 Max Diff. No.: -1.000E+00 Norm: 1.6780E-03
Iteration: 1910 Time: 1.910E+02 Max CFL: 1.387E+01 Max Diff. No.: -1.000E+00 Norm: 1.3915E-03
Iteration: 1920 Time: 1.920E+02 Max CFL: 1.388E+01 Max Diff. No.: -1.000E+00 Norm: 1.0838E-03
Iteration: 1930 Time: 1.930E+02 Max CFL: 1.388E+01 Max Diff. No.: -1.000E+00 Norm: 9.0528E-04
Iteration: 1940 Time: 1.940E+02 Max CFL: 1.387E+01 Max Diff. No.: -1.000E+00 Norm: 1.1377E-03
Iteration: 1950 Time: 1.950E+02 Max CFL: 1.388E+01 Max Diff. No.: -1.000E+00 Norm: 1.4727E-03
Iteration: 1960 Time: 1.960E+02 Max CFL: 1.387E+01 Max Diff. No.: -1.000E+00 Norm: 1.6229E-03
Iteration: 1970 Time: 1.970E+02 Max CFL: 1.388E+01 Max Diff. No.: -1.000E+00 Norm: 1.6072E-03
Iteration: 1980 Time: 1.980E+02 Max CFL: 1.387E+01 Max Diff. No.: -1.000E+00 Norm: 1.3256E-03
Iteration: 1990 Time: 1.990E+02 Max CFL: 1.388E+01 Max Diff. No.: -1.000E+00 Norm: 1.0886E-03
Iteration: 2000 Time: 2.000E+02 Max CFL: 1.388E+01 Max Diff. No.: -1.000E+00 Norm: 9.2072E-04
Writing solution file op.dat.
Iteration: 2010 Time: 2.010E+02 Max CFL: 1.387E+01 Max Diff. No.: -1.000E+00 Norm: 1.1236E-03
Iteration: 2020 Time: 2.020E+02 Max CFL: 1.389E+01 Max Diff. No.: -1.000E+00 Norm: 1.3463E-03
Iteration: 2030 Time: 2.030E+02 Max CFL: 1.387E+01 Max Diff. No.: -1.000E+00 Norm: 1.4901E-03
Iteration: 2040 Time: 2.040E+02 Max CFL: 1.389E+01 Max Diff. No.: -1.000E+00 Norm: 1.4674E-03
Iteration: 2050 Time: 2.050E+02 Max CFL: 1.387E+01 Max Diff. No.: -1.000E+00 Norm: 1.2350E-03
Iteration: 2060 Time: 2.060E+02 Max CFL: 1.388E+01 Max Diff. No.: -1.000E+00 Norm: 9.7215E-04
Iteration: 2070 Time: 2.070E+02 Max CFL: 1.388E+01 Max Diff. No.: -1.000E+00 Norm: 7.3510E-04
Iteration: 2080 Time: 2.080E+02 Max CFL: 1.387E+01 Max Diff. No.: -1.000E+00 Norm: 9.2631E-04
Iteration: 2090 Time: 2.090E+02 Max CFL: 1.388E+01 Max Diff. No.: -1.000E+00 Norm: 1.1485E-03
Iteration: 2100 Time: 2.100E+02 Max CFL: 1.387E+01 Max Diff. No.: -1.000E+00 Norm: 1.3304E-03
Iteration: 2110 Time: 2.110E+02 Max CFL: 1.388E+01 Max Diff. No.: -1.000E+00 Norm: 1.2821E-03
Iteration: 2120 Time: 2.120E+02 Max CFL: 1.387E+01 Max Diff. No.: -1.000E+00 Norm: 1.0554E-03
Iteration: 2130 Time: 2.130E+02 Max CFL: 1.388E+01 Max Diff. No.: -1.000E+00 Norm: 7.6179E-04
Iteration: 2140 Time: 2.140E+02 Max CFL: 1.388E+01 Max Diff. No.: -1.000E+00 Norm: 5.7059E-04
Iteration: 2150 Time: 2.150E+02 Max CFL: 1.387E+01 Max Diff. No.: -1.000E+00 Norm: 8.0358E-04
Iteration: 2160 Time: 2.160E+02 Max CFL: 1.388E+01 Max Diff. No.: -1.000E+00 Norm: 1.0106E-03
Iteration: 2170 Time: 2.170E+02 Max CFL: 1.387E+01 Max Diff. No.: -1.000E+00 Norm: 1.1733E-03
Iteration: 2180 Time: 2.180E+02 Max CFL: 1.388E+01 Max Diff. No.: -1.000E+00 Norm: 1.1121E-03
Iteration: 2190 Time: 2.190E+02 Max CFL: 1.387E+01 Max Diff. No.: -1.000E+00 Norm: 9.4580E-04
Iteration: 2200 Time: 2.200E+02 Max CFL: 1.388E+01 Max Diff. No.: -1.000E+00 Norm: 6.7588E-04
Iteration: 2210 Time: 2.210E+02 Max CFL: 1.388E+01 Max Diff. No.: -1.000E+00 Norm: 5.3513E-04
Iteration: 2220 Time: 2.220E+02 Max CFL: 1.387E+01 Max Diff. No.: -1.000E+00 Norm: 6.8955E-04
Iteration: 2230 Time: 2.230E+02 Max CFL: 1.389E+01 Max Diff. No.: -1.000E+00 Norm: 9.0262E-04
Iteration: 2240 Time: 2.240E+02 Max CFL: 1.387E+01 Max Diff. No.: -1.000E+00 Norm: 1.0676E-03
Iteration: 2250 Time: 2.250E+02 Max CFL: 1.388E+01 Max Diff. No.: -1.000E+00 Norm: 1.0301E-03
Iteration: 2260 Time: 2.260E+02 Max CFL: 1.387E+01 Max Diff. No.: -1.000E+00 Norm: 8.8867E-04
Iteration: 2270 Time: 2.270E+02 Max CFL: 1.388E+01 Max Diff. No.: -1.000E+00 Norm: 6.0438E-04
Iteration: 2280 Time: 2.280E+02 Max CFL: 1.388E+01 Max Diff. No.: -1.000E+00 Norm: 5.0241E-04
Iteration: 2290 Time: 2.290E+02 Max CFL: 1.387E+01 Max Diff. No.: -1.000E+00 Norm: 6.3679E-04
Iteration: 2300 Time: 2.300E+02 Max CFL: 1.388E+01 Max Diff. No.: -1.000E+00 Norm: 8.6614E-04
Iteration: 2310 Time: 2.310E+02 Max CFL: 1.387E+01 Max Diff. No.: -1.000E+00 Norm: 9.9506E-04
Iteration: 2320 Time: 2.320E+02 Max CFL: 1.388E+01 Max Diff. No.: -1.000E+00 Norm: 9.5214E-04
Iteration: 2330 Time: 2.330E+02 Max CFL: 1.388E+01 Max Diff. No.: -1.000E+00 Norm: 8.1654E-04
Iteration: 2340 Time: 2.340E+02 Max CFL: 1.388E+01 Max Diff. No.: -1.000E+00 Norm: 5.8223E-04
Iteration: 2350 Time: 2.350E+02 Max CFL: 1.388E+01 Max Diff. No.: -1.000E+00 Norm: 5.4310E-04
Iteration: 2360 Time: 2.360E+02 Max CFL: 1.388E+01 Max Diff. No.: -1.000E+00 Norm: 6.3081E-04
Iteration: 2370 Time: 2.370E+02 Max CFL: 1.388E+01 Max Diff. No.: -1.000E+00 Norm: 8.2481E-04
Iteration: 2380 Time: 2.380E+02 Max CFL: 1.387E+01 Max Diff. No.: -1.000E+00 Norm: 9.0706E-04
Iteration: 2390 Time: 2.390E+02 Max CFL: 1.388E+01 Max Diff. No.: -1.000E+00 Norm: 8.8761E-04
Iteration: 2400 Time: 2.400E+02 Max CFL: 1.388E+01 Max Diff. No.: -1.000E+00 Norm: 7.5756E-04
Iteration: 2410 Time: 2.410E+02 Max CFL: 1.388E+01 Max Diff. No.: -1.000E+00 Norm: 5.6006E-04
Iteration: 2420 Time: 2.420E+02 Max CFL: 1.388E+01 Max Diff. No.: -1.000E+00 Norm: 4.8920E-04
Iteration: 2430 Time: 2.430E+02 Max CFL: 1.388E+01 Max Diff. No.: -1.000E+00 Norm: 5.5084E-04
Iteration: 2440 Time: 2.440E+02 Max CFL: 1.389E+01 Max Diff. No.: -1.000E+00 Norm: 7.3963E-04
Iteration: 2450 Time: 2.450E+02 Max CFL: 1.387E+01 Max Diff. No.: -1.000E+00 Norm: 8.0862E-04
Iteration: 2460 Time: 2.460E+02 Max CFL: 1.389E+01 Max Diff. No.: -1.000E+00 Norm: 7.9415E-04
Iteration: 2470 Time: 2.470E+02 Max CFL: 1.388E+01 Max Diff. No.: -1.000E+00 Norm: 6.3448E-04
Iteration: 2480 Time: 2.480E+02 Max CFL: 1.388E+01 Max Diff. No.: -1.000E+00 Norm: 4.3683E-04
Iteration: 2490 Time: 2.490E+02 Max CFL: 1.388E+01 Max Diff. No.: -1.000E+00 Norm: 3.5460E-04
Iteration: 2500 Time: 2.500E+02 Max CFL: 1.388E+01 Max Diff. No.: -1.000E+00 Norm: 4.6126E-04
Writing solution file op.dat.
** Completed PETSc time integration **
Computed errors:
L1 Error : 0.0000000000000000E+00
L2 Error : 0.0000000000000000E+00
Linfinity Error : 0.0000000000000000E+00
Conservation Errors:
0.0000000000000000E+00
0.0000000000000000E+00
0.0000000000000000E+00
0.0000000000000000E+00
Solver runtime (in seconds): 5.4078647179999998E+03
Total runtime (in seconds): 5.4078814100000000E+03
Deallocating arrays.
Finished.