1D Linear Advection - Sine Wave

See 1D Linear Advection - Sine Wave to familiarize yourself with this case.

Location: hypar/Examples/1D/LinearAdvection/SineWave_libROM_DMD_Train (This directory contains all the input files needed to run this case.)

Governing equations: 1D Linear Advection Equation (linearadr.h)

Reduced Order Modeling: This example trains a DMD object and then predicts the solution using the DMD at the same times that the actual HyPar solution is written at.

References:

• Ghosh, D., Baeder, J. D., "Compact Reconstruction Schemes with Weighted ENO Limiting for Hyperbolic Conservation Laws", SIAM Journal on Scientific Computing, 34 (3), 2012, A1678–A1706

Domain: \(0 \le x < 1\), "periodic" (_PERIODIC_) boundary conditions

Initial solution: \(u\left(x,0\right) = \sin\left(2\pi x\right)\)

Numerical method:

• Spatial discretization (hyperbolic): 5th order CRWENO (Interp1PrimFifthOrderCRWENO())
• Time integration: 3rd order SSP RK3 (TimeRK(), RK_SSP3)

Reduced Order Modeling:

• Mode: train (libROMInterface::m_mode, _ROM_MODE_TRAIN_)
• Component Mode: monolithic (libROMInterface::m_comp_mode, _ROM_COMP_MODE_MONOLITHIC_)
• Type: Dynamic Mode Decomposition (DMD) with time windowing (libROMInterface::m_rom_type)
• Latent subspace dimension: 2 (DMDROMObject::m_rdim)

Input files required:

librom.inp

begin
  rdim                2
  sampling_frequency  1
  mode                train
end

solver.inp

begin
  ndims               1
  nvars               1
  size                80
  iproc               4
  ghost               3
  n_iter              200
  time_scheme         rk
  time_scheme_type    ssprk3
  hyp_space_scheme    crweno5
  conservation_check  yes
  dt                  0.005
  screen_op_iter      10
  file_op_iter        20
  ip_file_type        ascii
  op_file_format      binary
  op_overwrite        no
  model               linear-advection-diffusion-reaction
end

boundary.inp

2
periodic      0     1     0     0
periodic      0    -1     0     0

physics.inp

begin
  advection 1.0
end

lusolver.inp (optional)

begin
  reducedsolvetype  jacobi
  evaluate_norm     1
  maxiter           10
  atol              1e-12
  rtol              1e-10
  verbose           0
end

weno.inp (optional)

begin
  mapped        1
  borges        0
  yc            0
  no_limiting   0
  epsilon       0.000001
  p             2.0
  rc            0.3
  xi            0.001
end

To generate initial.inp, compile and run the following code in the run directory. Note: if the final time is an integer multiple of the time period, the file initial.inp can also be used as the exact solution exact.inp (i.e. create a sym link called exact.inp pointing to initial.inp, or just copy initial.inp to exact.inp).

#include <stdio.h>
#include <stdlib.h>
#include <math.h>
#include <string.h>


int main(){
  double pi = 4.0*atan(1.0);
    int NI,ndims;
  char ip_file_type[50];
  strcpy(ip_file_type,"ascii");
  FILE *in;
  printf("Reading file \"solver.inp\"...\n");
  in = fopen("solver.inp","r");
  if (!in) printf("Error: Input file \"solver.inp\" not found. Default values will be used.\n");
  else {
    char word[500];
    fscanf(in,"%s",word);
    if (!strcmp(word, "begin")){
      while (strcmp(word, "end")){
        fscanf(in,"%s",word);
        if (!strcmp(word, "ndims"))             fscanf(in,"%d",&ndims);
        else if (!strcmp(word, "size"))         fscanf(in,"%d",&NI);
        else if (!strcmp(word, "ip_file_type")) fscanf(in,"%s",ip_file_type);
      }
    } else printf("Error: Illegal format in solver.inp. Crash and burn!\n");
  }
  fclose(in);
  if (ndims != 1) {
    printf("ndims is not 1 in solver.inp. this code is to generate 1D initial conditions\n");
    return(0);
  }
    printf("Grid:\t\t\t%d\n",NI);

    int i;
    double dx = 1.0 / ((double)NI);

    double *x, *u;
    x = (double*) calloc (NI, sizeof(double));
    u = (double*) calloc (NI, sizeof(double));

    for (i = 0; i < NI; i++){
        x[i] = i*dx;
        u[i] = sin(2*pi*x[i]);
    }

  FILE *out;

  if (!strcmp(ip_file_type,"ascii")) {
    printf("Writing ASCII initial solution file initial.inp\n");
    out = fopen("initial.inp","w");
    for (i = 0; i < NI; i++)  fprintf(out,"%lf ",x[i]);
    fprintf(out,"\n");
      for (i = 0; i < NI; i++)  fprintf(out,"%lf ",u[i]);                       
    fprintf(out,"\n");
    fclose(out);
  } else if ((!strcmp(ip_file_type,"binary")) || (!strcmp(ip_file_type,"bin"))) {
    printf("Writing binary initial solution file initial.inp\n");
    out = fopen("initial.inp","wb");
    fwrite(x,sizeof(double),NI,out);
    fwrite(u,sizeof(double),NI,out);
    fclose(out);
  }

    free(x);
    free(u);

    return(0);
}

Output:

After running the code, there should be the following output files:

• 11 output files op_00000.bin, op_00001.bin, ... op_00010.bin; these are the HyPar solutions.
• 11 output files op_rom_00000.bin, op_rom_00001.bin, ... op_rom_00010.bin; these are the predicted solutions from the DMD object(s).

The first of each of these file sets is the solution at \(t=0\) and the final one is the solution at \(t=1\). Since HyPar::op_overwrite is set to no in solver.inp, a separate file is written for solutions at each output time. All the files are binary (HyPar::op_file_format is set to binary in solver.inp).

The provided Python script (plotSolution.py) can be used to generate plots from the binary files that compare the HyPar and DMD solutions. Alternatively, HyPar::op_file_format can be set to text, and GNUPlot or something similar can be used to plot the resulting text files.

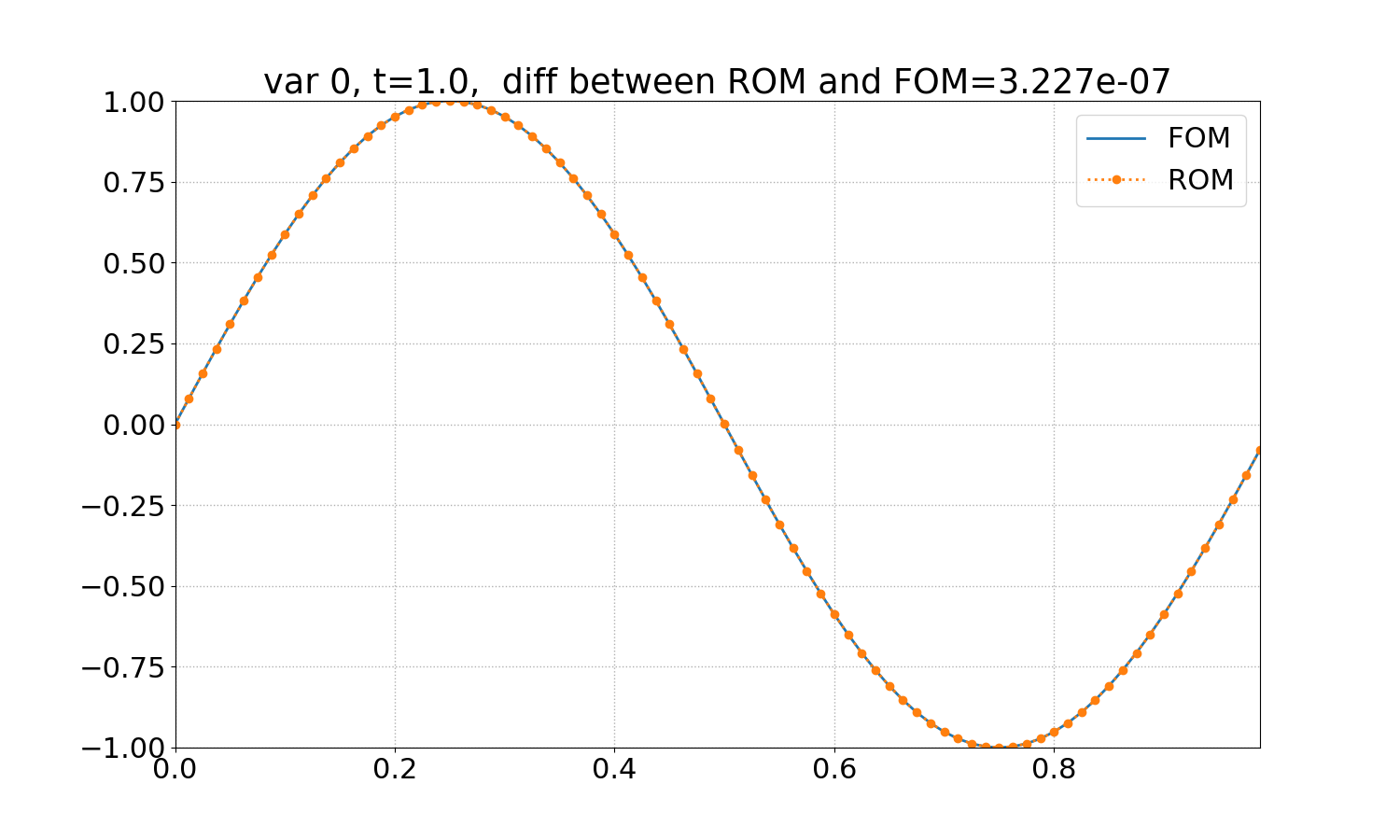
The following plot shows the final solution - FOM (full-order model) refers to the HyPar solution, ROM (reduced-order model) refers to the DMD solution.

The L1, L2, and Linf norms of the diff between the HyPar and ROM solution at the final time are calculated and reported on screen (see below) as well as pde_rom_diff.dat:

  80    4 5.0000000000000001E-03  2.9065523787146478E-07 3.2037250962276641E-07 4.1231337540346448E-07   1.6993039999999999E+00 2.4370970000000001E+00

The numbers are: number of grid points (HyPar::dim_global), number of processors (MPIVariables::iproc), time step size (HyPar::dt), L1, L2, and L-infinity norms of the diff (HyPar::rom_diff_norms), solver wall time (seconds) (i.e., not accounting for initialization, and cleaning up), and total wall time.

By default, the code will write the trained DMD object(s) to files in a subdirectory (DMDROMObject::m_dirname - default value is "DMD"). If the subdirectory does not exist, the code may not report an error (or give some HDF5 file-writing error); the DMD objects will not be written! If the subdirectory exists, several files will exist after the simulation is complete - they are in a format that is readable by libROM.

Expected screen output:

HyPar - Parallel (MPI) version with 4 processes
Compiled with PETSc time integration.
Allocated simulation object(s).
Reading solver inputs from file "solver.inp".
  No. of dimensions                          : 1
  No. of variables                           : 1
  Domain size                                : 80 
  Processes along each dimension             : 4 
  Exact solution domain size                 : 80 
  No. of ghosts pts                          : 3
  No. of iter.                               : 200
  Restart iteration                          : 0
  Time integration scheme                    : rk (ssprk3)
  Spatial discretization scheme (hyperbolic) : crweno5
  Split hyperbolic flux term?                : no
  Interpolation type for hyperbolic term     : characteristic
  Spatial discretization type   (parabolic ) : nonconservative-1stage
  Spatial discretization scheme (parabolic ) : 2
  Time Step                                  : 5.000000E-03
  Check for conservation                     : yes
  Screen output iterations                   : 10
  File output iterations                     : 20
  Initial solution file type                 : ascii
  Initial solution read mode                 : serial
  Solution file write mode                   : serial
  Solution file format                       : binary
  Overwrite solution file                    : no
  Physical model                             : linear-advection-diffusion-reaction
Partitioning domain and allocating data arrays.
Reading array from ASCII file initial.inp (Serial mode).
Volume integral of the initial solution:
 0:  -5.5511151231257827E-17
Reading boundary conditions from boundary.inp.
  Boundary                       periodic:  Along dimension  0 and face +1
  Boundary                       periodic:  Along dimension  0 and face -1
2 boundary condition(s) read.
Initializing solvers.
Reading WENO parameters from weno.inp.
Initializing physics. Model = "linear-advection-diffusion-reaction"
Reading physical model inputs from file "physics.inp".
Setting up time integration.
Setting up libROM interface.
libROM inputs and parameters:
  reduced model dimensionality:  2
  sampling frequency:  1
  mode: train
  type: DMD
  save to file: true
  local vector size: 20
libROM DMD inputs:
  number of samples per window:   2147483647
  directory name for DMD onjects: DMD
Solving in time (from 0 to 200 iterations)
Writing solution file op_00000.bin.
DMDROMObject::takeSample() - creating new DMD object, t=0.000000 (total: 1).
iter=     10  t=5.000E-02  CFL=4.000E-01  norm=2.2213E-02  wctime: 3.2E-04 (s)    cons_err=4.3368E-19
iter=     20  t=1.000E-01  CFL=4.000E-01  norm=2.2213E-02  wctime: 2.9E-04 (s)    cons_err=4.3368E-19
Writing solution file op_00001.bin.
iter=     30  t=1.500E-01  CFL=4.000E-01  norm=2.2213E-02  wctime: 3.2E-04 (s)    cons_err=2.5587E-17
iter=     40  t=2.000E-01  CFL=4.000E-01  norm=2.2213E-02  wctime: 3.2E-04 (s)    cons_err=2.5587E-17
Writing solution file op_00002.bin.
iter=     50  t=2.500E-01  CFL=4.000E-01  norm=2.2213E-02  wctime: 2.6E-04 (s)    cons_err=2.1684E-18
iter=     60  t=3.000E-01  CFL=4.000E-01  norm=2.2213E-02  wctime: 2.8E-04 (s)    cons_err=6.5486E-17
Writing solution file op_00003.bin.
iter=     70  t=3.500E-01  CFL=4.000E-01  norm=2.2213E-02  wctime: 3.0E-04 (s)    cons_err=8.1098E-17
iter=     80  t=4.000E-01  CFL=4.000E-01  norm=2.2213E-02  wctime: 3.1E-04 (s)    cons_err=5.3343E-17
Writing solution file op_00004.bin.
iter=     90  t=4.500E-01  CFL=4.000E-01  norm=2.2213E-02  wctime: 3.1E-04 (s)    cons_err=1.6176E-16
iter=    100  t=5.000E-01  CFL=4.000E-01  norm=2.2213E-02  wctime: 3.0E-04 (s)    cons_err=6.0715E-17
Writing solution file op_00005.bin.
iter=    110  t=5.500E-01  CFL=4.000E-01  norm=2.2213E-02  wctime: 3.1E-04 (s)    cons_err=4.8139E-17
iter=    120  t=6.000E-01  CFL=4.000E-01  norm=2.2213E-02  wctime: 2.8E-04 (s)    cons_err=4.9006E-17
Writing solution file op_00006.bin.
iter=    130  t=6.500E-01  CFL=4.000E-01  norm=2.2213E-02  wctime: 3.0E-04 (s)    cons_err=4.9006E-17
iter=    140  t=7.000E-01  CFL=4.000E-01  norm=2.2213E-02  wctime: 2.8E-04 (s)    cons_err=1.0625E-16
Writing solution file op_00007.bin.
iter=    150  t=7.500E-01  CFL=4.000E-01  norm=2.2213E-02  wctime: 2.5E-04 (s)    cons_err=7.6762E-17
iter=    160  t=8.000E-01  CFL=4.000E-01  norm=2.2213E-02  wctime: 3.0E-04 (s)    cons_err=8.2399E-18
Writing solution file op_00008.bin.
iter=    170  t=8.500E-01  CFL=4.000E-01  norm=2.2213E-02  wctime: 2.7E-04 (s)    cons_err=2.1250E-17
iter=    180  t=9.000E-01  CFL=4.000E-01  norm=2.2213E-02  wctime: 2.7E-04 (s)    cons_err=4.7271E-17
Writing solution file op_00009.bin.
iter=    190  t=9.500E-01  CFL=4.000E-01  norm=2.2213E-02  wctime: 3.0E-04 (s)    cons_err=4.5536E-17
iter=    200  t=1.000E+00  CFL=4.000E-01  norm=2.2213E-02  wctime: 2.8E-04 (s)    cons_err=1.5699E-16
Completed time integration (Final time: 1.000000), total wctime: 0.718540 (seconds).
Reading array from ASCII file exact.inp (Serial mode).
Writing solution file op_00010.bin.
libROM: Training ROM.
DMDRomObject::train() - training DMD object 0 with 200 samples.
Using 2 basis vectors out of 80.
libROM: wallclock time: 0.059403 (seconds).
libROM: Predicting solution at time 0.0000e+00 using ROM.
libROM:   wallclock time: 0.000077 (seconds).
Writing solution file op_rom_00000.bin.
libROM: Predicting solution at time 1.0000e-01 using ROM.
libROM:   wallclock time: 0.000037 (seconds).
Writing solution file op_rom_00001.bin.
libROM: Predicting solution at time 2.0000e-01 using ROM.
libROM:   wallclock time: 0.000030 (seconds).
Writing solution file op_rom_00002.bin.
libROM: Predicting solution at time 3.0000e-01 using ROM.
libROM:   wallclock time: 0.000031 (seconds).
Writing solution file op_rom_00003.bin.
libROM: Predicting solution at time 4.0000e-01 using ROM.
libROM:   wallclock time: 0.000033 (seconds).
Writing solution file op_rom_00004.bin.
libROM: Predicting solution at time 5.0000e-01 using ROM.
libROM:   wallclock time: 0.000032 (seconds).
Writing solution file op_rom_00005.bin.
libROM: Predicting solution at time 6.0000e-01 using ROM.
libROM:   wallclock time: 0.000030 (seconds).
Writing solution file op_rom_00006.bin.
libROM: Predicting solution at time 7.0000e-01 using ROM.
libROM:   wallclock time: 0.000047 (seconds).
Writing solution file op_rom_00007.bin.
libROM: Predicting solution at time 8.0000e-01 using ROM.
libROM:   wallclock time: 0.000030 (seconds).
Writing solution file op_rom_00008.bin.
libROM: Predicting solution at time 9.0000e-01 using ROM.
libROM:   wallclock time: 0.000030 (seconds).
Writing solution file op_rom_00009.bin.
libROM: Predicting solution at time 1.0000e+00 using ROM.
libROM:   wallclock time: 0.000029 (seconds).
libROM:   Calculating diff between PDE and ROM solutions.
Writing solution file op_rom_00010.bin.
libROM: total prediction/query wallclock time: 0.000406 (seconds).
libROMInterface::saveROM() - saving ROM objects.
  Saving DMD object with filename root DMD/dmdobj_0000.
Computed errors for domain 0:
  L1         Error           : 8.1564188969988377E-06
  L2         Error           : 8.1563255924379997E-06
  Linfinity  Error           : 8.4640413008374438E-06
Conservation Errors:
    1.5699247457590104E-16
Norms of the diff between ROM and PDE solutions for domain 0:
  L1         Norm            : 2.9065523787146478E-07
  L2         Norm            : 3.2037250962276641E-07
  Linfinity  Norm            : 4.1231337540346448E-07
Solver runtime (in seconds): 2.4540210000000000E+00
Total  runtime (in seconds): 3.2191299999999998E+00
Deallocating arrays.
Finished.