HyPar  1.0
Finite-Difference Hyperbolic-Parabolic PDE Solver on Cartesian Grids
1D Euler Equations - Shu-Osher Problem (Time Windowed DMD)

See 1D Euler Equations - Shu-Osher Problem to familiarize yourself with this case.

Description:

Location: hypar/Examples/1D/Euler1D/ShuOsherProblem_libROM_DMD_Train (This directory contains all the input files needed to run this case. If there is a Run.m, run it in MATLAB to quickly set up, run, and visualize the example).

Governing equations: 1D Euler equations (euler1d.h)

Reduced Order Modeling: This example trains a DMD object and then predicts the solution using the DMD at the same times that the actual HyPar solution is written at.

References:

  • C.-W. Shu and S. Osher, "Efficient implementation of essentially non-oscillatory schemes ,II," J. Comput. Phys., 83 (1989), pp. 32–78

Domain: \(-5 \le x \le 5\), "extrapolate" (_EXTRAPOLATE_) boundary conditions

Initial Solution:

  • \( -5 \le x < -4\): \(\rho = 27/7, u = 4\sqrt{35}/7, p = 31/3\)
  • \( -4 \le x \le 5\): \(\rho = 1 + 0.2\sin\left(5x\right), u = 0, p = 1\)

Numerical Method:

Reduced Order Modeling:

Input files required:

librom.inp:

begin
rdim 16
sampling_frequency 1
mode train
dmd_num_win_samples 60
end

solver.inp:

begin
ndims 1
nvars 3
size 201
iproc 1
ghost 3
n_iter 360
time_scheme rk
time_scheme_type 44
hyp_space_scheme weno5
hyp_interp_type characteristic
conservation_check yes
dt 0.005
screen_op_iter 18
file_op_iter 36
op_file_format binary
op_overwrite no
model euler1d
end

boundary.inp

2
extrapolate 0 1 0 0
extrapolate 0 -1 0 0

physics.inp

begin
gamma 1.4
upwinding rf-char
end

weno.inp (optional)

begin
mapped 1
borges 0
yc 0
no_limiting 0
epsilon 0.000001
p 2.0
rc 0.3
xi 0.001
end

To generate initial.inp, compile and run the following code in the run directory:

#include <stdio.h>
#include <stdlib.h>
#include <math.h>
#include <string.h>
int main(){
int NI=101,ndims=1;
FILE *in;
char ip_file_type[50];
strcpy(ip_file_type,"ascii");
printf("Reading file \"solver.inp\"...\n");
in = fopen("solver.inp","r");
if (!in) {
printf("Error: Input file \"solver.inp\" not found. Default values will be used.\n");
} else {
char word[500];
fscanf(in,"%s",word);
if (!strcmp(word, "begin")){
while (strcmp(word, "end")){
fscanf(in,"%s",word);
if (!strcmp(word, "ndims")) fscanf(in,"%d",&ndims);
else if (!strcmp(word, "size")) fscanf(in,"%d",&NI);
else if (!strcmp(word, "ip_file_type")) fscanf(in,"%s",ip_file_type);
}
} else {
printf("Error: Illegal format in solver.inp. Crash and burn!\n");
}
}
fclose(in);
if (ndims != 1) {
printf("ndims is not 1 in solver.inp. this code is to generate 1D initial conditions\n");
return(0);
}
printf("Grid:\t\t\t%d\n",NI);
int i;
double dx = 10.0 / ((double)(NI-1));
double *x, *rho,*rhou,*e;
x = (double*) calloc (NI, sizeof(double));
rho = (double*) calloc (NI, sizeof(double));
rhou = (double*) calloc (NI, sizeof(double));
e = (double*) calloc (NI, sizeof(double));
for (i = 0; i < NI; i++){
x[i] = -5.0 + i*dx;
double RHO,U,P;
if (x[i] < -4.0) {
RHO = 27.0/7.0;
U = 4.0*sqrt(35.0)/9.0;
P = 31.0/3.0;
} else {
RHO = 1.0+0.2*sin(5*x[i]);
U = 0;
P = 1;
}
rho[i] = RHO;
rhou[i] = RHO*U;
e[i] = P/0.4 + 0.5*RHO*U*U;
}
if (!strcmp(ip_file_type,"ascii")) {
FILE *out;
out = fopen("initial.inp","w");
for (i = 0; i < NI; i++) fprintf(out,"%lf ",x[i]);
fprintf(out,"\n");
for (i = 0; i < NI; i++) fprintf(out,"%lf ",rho[i]);
fprintf(out,"\n");
for (i = 0; i < NI; i++) fprintf(out,"%lf ",rhou[i]);
fprintf(out,"\n");
for (i = 0; i < NI; i++) fprintf(out,"%lf ",e[i]);
fprintf(out,"\n");
fclose(out);
} else if ((!strcmp(ip_file_type,"binary")) || (!strcmp(ip_file_type,"bin"))) {
printf("Error: Writing binary initial solution file not implemented. ");
printf("Please choose ip_file_type in solver.inp as \"ascii\".\n");
}
free(x);
free(rho);
free(rhou);
free(e);
return(0);
}

Output:

After running the code, there should be the following output files:

  • 11 output files op_00000.bin, op_00001.bin, ... op_00010.bin; these are the HyPar solutions.
  • 11 output files op_rom_00000.bin, op_rom_00001.bin, ... op_rom_00010.bin; these are the predicted solutions from the DMD object(s).

The first of each of these file sets is the solution at \(t=0\) and the final one is the solution at \(t=1.8\). Since HyPar::op_overwrite is set to no in solver.inp, a separate file is written for solutions at each output time. All the files are binary (HyPar::op_file_format is set to binary in solver.inp).

The provided Python script (plotSolution.py) can be used to generate plots from the binary files that compare the HyPar and DMD solutions. It will plot the 3 conserved variables - density, momentum, and energy. Alternatively, HyPar::op_file_format can be set to text, and GNUPlot or something similar can be used to plot the resulting text files.

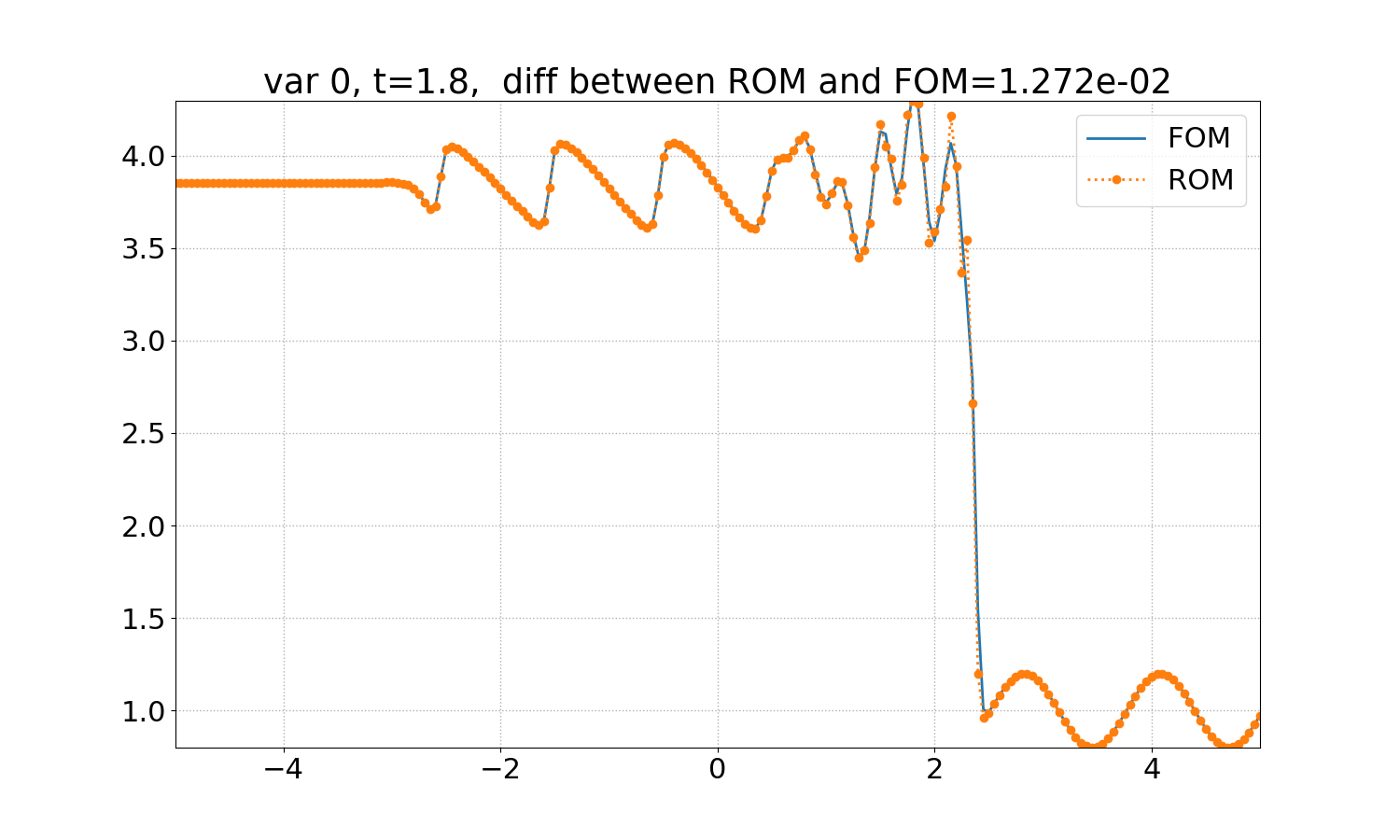
The following plot shows the final solution (density) - FOM (full-order model) refers to the HyPar solution, ROM (reduced-order model) refers to the DMD solution.

Solution_1DShuOsherProblem_libROM_DMD.png

The L1, L2, and Linf norms of the diff between the HyPar and ROM solution at the final time are calculated and reported on screen (see below) as well as pde_rom_diff.dat:

201 1 5.0000000000000001E-03 5.3652606894055016E-03 1.8844715702469858E-02 1.3738460264388241E-01 8.3716869999999997E+00 8.3836230000000000E+00

The numbers are: number of grid points (HyPar::dim_global), number of processors (MPIVariables::iproc), time step size (HyPar::dt), L1, L2, and L-infinity norms of the diff (HyPar::rom_diff_norms), solver wall time (seconds) (i.e., not accounting for initialization, and cleaning up), and total wall time.

By default, the code will write the trained DMD object(s) to files in a subdirectory (DMDROMObject::m_dirname - default value is "DMD"). If the subdirectory does not exist, the code may not report an error (or give some HDF5 file-writing error); the DMD objects will not be written! If the subdirectory exists, several files will exist after the simulation is complete - they are in a format that is readable by libROM.

Expected screen output:

HyPar - Parallel (MPI) version with 1 processes
Compiled with PETSc time integration.
Allocated simulation object(s).
Reading solver inputs from file "solver.inp".
No. of dimensions : 1
No. of variables : 3
Domain size : 201
Processes along each dimension : 1
Exact solution domain size : 201
No. of ghosts pts : 3
No. of iter. : 360
Restart iteration : 0
Time integration scheme : rk (44)
Spatial discretization scheme (hyperbolic) : weno5
Split hyperbolic flux term? : no
Interpolation type for hyperbolic term : characteristic
Spatial discretization type (parabolic ) : nonconservative-1stage
Spatial discretization scheme (parabolic ) : 2
Time Step : 5.000000E-03
Check for conservation : yes
Screen output iterations : 18
File output iterations : 36
Initial solution file type : ascii
Initial solution read mode : serial
Solution file write mode : serial
Solution file format : binary
Overwrite solution file : no
Physical model : euler1d
Partitioning domain and allocating data arrays.
Reading array from ASCII file initial.inp (Serial mode).
Volume integral of the initial solution:
0: 1.2878713250000002E+01
1: 1.0141851000000001E+01
2: 6.1791666999999997E+01
Reading boundary conditions from boundary.inp.
Boundary extrapolate: Along dimension 0 and face +1
Boundary extrapolate: Along dimension 0 and face -1
2 boundary condition(s) read.
Initializing solvers.
Reading WENO parameters from weno.inp.
Initializing physics. Model = "euler1d"
Reading physical model inputs from file "physics.inp".
Setting up time integration.
Setting up libROM interface.
libROM inputs and parameters:
reduced model dimensionality: 16
sampling frequency: 1
mode: train
type: DMD
save to file: true
local vector size: 603
libROM DMD inputs:
number of samples per window: 60
directory name for DMD onjects: DMD
Solving in time (from 0 to 360 iterations)
Writing solution file op_00000.bin.
DMDROMObject::takeSample() - creating new DMD object, t=0.000000 (total: 1).
iter= 18 t=9.000E-02 CFL=4.675E-01 norm=6.4460E-01 wctime: 4.3E-03 (s) cons_err=3.4641E-16
iter= 36 t=1.800E-01 CFL=4.666E-01 norm=6.4865E-01 wctime: 3.3E-03 (s) cons_err=7.9302E-16
Writing solution file op_00001.bin.
iter= 54 t=2.700E-01 CFL=4.662E-01 norm=6.2513E-01 wctime: 3.3E-03 (s) cons_err=4.7516E-16
DMDROMObject::takeSample() - creating new DMD object, t=0.300000 (total: 2).
iter= 72 t=3.600E-01 CFL=4.661E-01 norm=6.1868E-01 wctime: 3.4E-03 (s) cons_err=7.8730E-16
Writing solution file op_00002.bin.
iter= 90 t=4.500E-01 CFL=4.705E-01 norm=5.9830E-01 wctime: 3.3E-03 (s) cons_err=5.6648E-16
iter= 108 t=5.400E-01 CFL=4.706E-01 norm=6.4966E-01 wctime: 3.3E-03 (s) cons_err=2.0337E-15
Writing solution file op_00003.bin.
DMDROMObject::takeSample() - creating new DMD object, t=0.600000 (total: 3).
iter= 126 t=6.300E-01 CFL=4.673E-01 norm=6.6514E-01 wctime: 3.3E-03 (s) cons_err=1.6098E-15
iter= 144 t=7.200E-01 CFL=4.703E-01 norm=5.9784E-01 wctime: 3.5E-03 (s) cons_err=2.0045E-15
Writing solution file op_00004.bin.
iter= 162 t=8.100E-01 CFL=4.706E-01 norm=6.3279E-01 wctime: 3.6E-03 (s) cons_err=4.7302E-15
iter= 180 t=9.000E-01 CFL=4.734E-01 norm=6.4860E-01 wctime: 3.3E-03 (s) cons_err=3.1243E-15
Writing solution file op_00005.bin.
DMDROMObject::takeSample() - creating new DMD object, t=0.900000 (total: 4).
iter= 198 t=9.900E-01 CFL=4.668E-01 norm=6.2587E-01 wctime: 3.4E-03 (s) cons_err=1.5700E-15
iter= 216 t=1.080E+00 CFL=4.694E-01 norm=6.0359E-01 wctime: 3.3E-03 (s) cons_err=1.4805E-15
Writing solution file op_00006.bin.
iter= 234 t=1.170E+00 CFL=4.710E-01 norm=6.2767E-01 wctime: 4.4E-03 (s) cons_err=3.2547E-15
DMDROMObject::takeSample() - creating new DMD object, t=1.200000 (total: 5).
iter= 252 t=1.260E+00 CFL=4.743E-01 norm=6.7354E-01 wctime: 3.7E-03 (s) cons_err=4.6633E-15
Writing solution file op_00007.bin.
iter= 270 t=1.350E+00 CFL=4.673E-01 norm=6.4634E-01 wctime: 3.4E-03 (s) cons_err=1.8540E-15
iter= 288 t=1.440E+00 CFL=4.719E-01 norm=6.2678E-01 wctime: 3.3E-03 (s) cons_err=1.0414E-15
Writing solution file op_00008.bin.
DMDROMObject::takeSample() - creating new DMD object, t=1.500000 (total: 6).
iter= 306 t=1.530E+00 CFL=4.723E-01 norm=6.2222E-01 wctime: 3.3E-03 (s) cons_err=2.3247E-15
iter= 324 t=1.620E+00 CFL=4.735E-01 norm=6.4101E-01 wctime: 3.3E-03 (s) cons_err=5.6663E-15
Writing solution file op_00009.bin.
iter= 342 t=1.710E+00 CFL=4.684E-01 norm=6.3322E-01 wctime: 3.4E-03 (s) cons_err=3.3712E-15
iter= 360 t=1.800E+00 CFL=4.717E-01 norm=5.9076E-01 wctime: 3.6E-03 (s) cons_err=4.4968E-15
Completed time integration (Final time: 1.800000), total wctime: 1.267065 (seconds).
Writing solution file op_00010.bin.
libROM: Training ROM.
DMDROMObject::train() - training DMD object 0 with 61 samples.
Using 16 basis vectors out of 60.
DMDROMObject::train() - training DMD object 1 with 61 samples.
Using 16 basis vectors out of 60.
DMDROMObject::train() - training DMD object 2 with 61 samples.
Using 16 basis vectors out of 60.
DMDROMObject::train() - training DMD object 3 with 61 samples.
Using 16 basis vectors out of 60.
DMDROMObject::train() - training DMD object 4 with 61 samples.
Using 16 basis vectors out of 60.
DMDROMObject::train() - training DMD object 5 with 60 samples.
Using 16 basis vectors out of 59.
libROM: total training wallclock time: 0.245015 (seconds).
libROM: Predicting solution at time 0.0000e+00 using ROM.
libROM: wallclock time: 0.006054 (seconds).
Writing solution file op_rom_00000.bin.
libROM: Predicting solution at time 1.8000e-01 using ROM.
libROM: wallclock time: 0.006032 (seconds).
Writing solution file op_rom_00001.bin.
libROM: Predicting solution at time 3.6000e-01 using ROM.
libROM: wallclock time: 0.006717 (seconds).
Writing solution file op_rom_00002.bin.
libROM: Predicting solution at time 5.4000e-01 using ROM.
libROM: wallclock time: 0.006902 (seconds).
Writing solution file op_rom_00003.bin.
libROM: Predicting solution at time 7.2000e-01 using ROM.
libROM: wallclock time: 0.006423 (seconds).
Writing solution file op_rom_00004.bin.
libROM: Predicting solution at time 9.0000e-01 using ROM.
libROM: wallclock time: 0.006050 (seconds).
Writing solution file op_rom_00005.bin.
libROM: Predicting solution at time 1.0800e+00 using ROM.
libROM: wallclock time: 0.006048 (seconds).
Writing solution file op_rom_00006.bin.
libROM: Predicting solution at time 1.2600e+00 using ROM.
libROM: wallclock time: 0.007260 (seconds).
Writing solution file op_rom_00007.bin.
libROM: Predicting solution at time 1.4400e+00 using ROM.
libROM: wallclock time: 0.006077 (seconds).
Writing solution file op_rom_00008.bin.
libROM: Predicting solution at time 1.6200e+00 using ROM.
libROM: wallclock time: 0.006125 (seconds).
Writing solution file op_rom_00009.bin.
libROM: Predicting solution at time 1.8000e+00 using ROM.
libROM: wallclock time: 0.006544 (seconds).
libROM: Calculating diff between PDE and ROM solutions.
Writing solution file op_rom_00010.bin.
libROM: total prediction/query wallclock time: 0.070232 (seconds).
libROMInterface::saveROM() - saving ROM objects.
Saving DMD object with filename root DMD/dmdobj_0000.
Saving DMD object with filename root DMD/dmdobj_0001.
Saving DMD object with filename root DMD/dmdobj_0002.
Saving DMD object with filename root DMD/dmdobj_0003.
Saving DMD object with filename root DMD/dmdobj_0004.
Saving DMD object with filename root DMD/dmdobj_0005.
Conservation Errors:
4.1378904978731091E-16
4.0284763901782583E-15
1.9548309819707087E-15
Norms of the diff between ROM and PDE solutions for domain 0:
L1 Norm : 5.3652606894055016E-03
L2 Norm : 1.8844715702469858E-02
Linfinity Norm : 1.3738460264388241E-01
Solver runtime (in seconds): 8.3716869999999997E+00
Total runtime (in seconds): 8.3836230000000000E+00
Deallocating arrays.
Finished.