See Steady, incompressible, viscous flow around a cylinder to familiarize yourself with this case. This example uses a DMD object that has already been trained (see 3D Navier-Stokes - Steady, incompressible, viscous flow around a cylinder (Time-Windowed DMD)).
Location: hypar/Examples/3D/NavierStokes3D/2D_Cylinder/Steady_Viscous_Incompressible_libROM_DMD_Predict
Governing equations: 3D Navier-Stokes Equations (navierstokes3d.h)
Reduced Order Modeling: This example predicts the solution from a trained DMD object. The code does not solve the PDE by discretizing in space and integrating in time.
Domain: The domain consists of a fine uniform grid around the cylinder defined by [-2,6] X [-2,2], and a stretched grid beyond this zone. Note: This is a 2D flow simulated using a 3-dimensional setup by taking the length of the domain along z to be very small and with only 3 grid points (the domain size along z must be smaller than the cylinder length).
Geometry: A cylinder of radius 1.0 centered at (0,0) (hypar/Examples/STLGeometries/cylinder.stl)
See Steady, incompressible, viscous flow around a cylinder for pictures showing the domain and geometry.
Boundary conditions:
Reference:
- Taneda, S., "Experimental Investigation of the Wakes behind Cylinders and Plates at Low
Reynolds Numbers," Journal of the Physical Society of Japan, Vol. 11, 302–307, 1956.
- Dennis, S. C. R., Chang, G.-Z., "Numerical solutions for steady flow past a circular
cylinder at Reynolds numbers up to 100", Journal of Fluid Mechanics, 42 (3), 1970, pp. 471-489.
Initial solution: \(\rho=1, u=0.1, v=w=0, p=1/\gamma\) everywhere in the domain.
Other parameters:
Reduced Order Modeling:
Note:
In this mode, HyPar will run just like an usual PDE simulation, except that it will swap out the numerical spatial discretization and time integration with the ROM-based prediction. The input files and output files will be the same as a regular simulation with the following comments:
- Numerical method inputs are ignored (eg. those that specify spatial discretization and time integration methods).
- In solver.inp, the values for dt, n_iter, and file_op_iter is used only to compute the simulation times at which to compute and write the solution. The time step size, dt, need not respect any CFL criterion.
- HyPar::ConservationCheck is set to "no" since it is not possible to compute conservation loss for a general domain (because boundary fluxes are not being computed).
Input files required:
DMD Object(s) :
The trained DMD object(s) must be located in the directory specified in librom.inp as dmd_dirname (DMDROMObject::m_dirname). For this example, they were generated using 3D Navier-Stokes - Steady, incompressible, viscous flow around a cylinder (Time-Windowed DMD).
librom.inp
begin
mode predict
dmd_dirname DMD
end
solver.inp
begin
ndims 3
nvars 5
size 200 96 3
iproc 8 4 1
ghost 3
n_iter 1
par_space_type nonconservative-2stage
dt 1000
file_op_iter 1
ip_file_type binary
op_file_format binary
op_overwrite yes
model navierstokes3d
immersed_body cylinder.stl
end
boundary.inp
6
subsonic-inflow 0 1 0 0 -9999.0 9999.0 -9999.0 9999.0
1.0 0.1 0.0 0.0
subsonic-outflow 0 -1 0 0 -9999.0 9999.0 -9999.0 9999.0
0.7142857142857143
subsonic-ambivalent 1 1 -9999.0 9999.0 0 0 -9999.0 9999.0
1.0 0.1 0.0 0.0 0.7142857142857143
subsonic-ambivalent 1 -1 -9999.0 9999.0 0 0 -9999.0 9999.0
1.0 0.1 0.0 0.0 0.7142857142857143
periodic 2 1 -9999.0 9999.0 -9999.0 9999.0 0 0
periodic 2 -1 -9999.0 9999.0 -9999.0 9999.0 0 0
physics.inp : The following file specifies a Reynolds number of 10 (corresponding to \(Re_D\) of 20). To try other Reynolds numbers, change it here.
begin
gamma 1.4
upwinding roe
Pr 0.72
Minf 0.1
Re 10
end
cylinder.stl : the filename "cylinder.stl" must match the input for immersed_body in solver.inp.
Located at hypar/Examples/STLGeometries/cylinder.stl
To generate initial.inp (initial solution), compile and run the following code in the run directory.
#include <stdio.h>
#include <stdlib.h>
#include <math.h>
#include <string.h>
{
const double GAMMA = 1.4;
int NI,NJ,NK,ndims;
char ip_file_type[50];
FILE *in;
strcpy(ip_file_type,"ascii");
printf("Reading file \"solver.inp\"...\n");
in = fopen("solver.inp","r");
if (!in) {
printf("Error: Input file \"solver.inp\" not found.\n");
return(0);
} else {
char word[500];
fscanf(in,"%s",word);
if (!strcmp(word, "begin")){
while (strcmp(word, "end")){
fscanf(in,"%s",word);
if (!strcmp(word, "ndims")) {
fscanf(in,"%d",&ndims);
} else if (!strcmp(word, "size" )) {
fscanf(in,"%d",&NI);
fscanf(in,"%d",&NJ);
fscanf(in,"%d",&NK);
} else if (!strcmp(word, "ip_file_type")) {
fscanf(in,"%s",ip_file_type);
}
}
} else {
printf("Error: Illegal format in solver.inp. Crash and burn!\n");
return(0);
}
}
fclose(in);
if (ndims != 3) {
printf("Error: ndims is not 3 in solver.inp.\n");
return(0);
}
printf("Grid: %3d x %3d x %3d.\n",NI,NJ,NK);
double Lx = 8.0;
double Ly = 4.0;
double sf_x1 = 1.15;
double sf_x2 = 1.20;
double sf_y = 1.4;
int i,j,k;
double u = 0.1,
v = 0.0,
w = 0.0,
rho = 1.0,
P = 1.0/GAMMA;
double *x, *y, *z, *U;
double dx, dy, dz;
FILE *out;
x = (double*) calloc (NI , sizeof(double));
y = (double*) calloc (NJ , sizeof(double));
z = (double*) calloc (NK , sizeof(double));
U = (double*) calloc (5*NI*NJ*NK, sizeof(double));
x[NI/8] = -Lx/4;
x[7*NI/8] = 3*Lx/4;
dx = Lx / ((double)(6*NI/8));
for (i = NI/8 ; i < 7*NI/8; i++) x[i] = x[NI/8] + dx * (i-NI/8);
for (i = 7*NI/8; i < NI ; i++) x[i] = x[i-1] + sf_x2 * (x[i-1] - x[i-2]);
for (i = NI/8-1; i >= 0 ; i--) x[i] = x[i+1] - sf_x1 * (x[i+2] - x[i+1]);
y[NJ/8] = -Ly/2;
y[7*NJ/8] = Ly/2;
dy = Ly / ((double)(6*NJ/8));
for (j = NJ/8 ; j < 7*NJ/8; j++) y[j] = y[NJ/8] + dy * (j-NJ/8);
for (j = 7*NJ/8; j < NJ ; j++) y[j] = y[j-1] + sf_y * (y[j-1] - y[j-2]);
for (j = NJ/8-1; j >= 0 ; j--) y[j] = y[j+1] - sf_y * (y[j+2] - y[j+1]);
dz = 0.5 * (dx +dy);
for (k = 0; k < NK; k++) z[k] = (k-NK/2) * dz;
for (i = 0; i < NI; i++){
for (j = 0; j < NJ; j++){
for (k = 0; k < NK; k++){
int p = i + NI*j + NI*NJ*k;
U[5*p+0] = rho;
U[5*p+1] = rho*u;
U[5*p+2] = rho*v;
U[5*p+3] = rho*w;
U[5*p+4] = P/(GAMMA-1.0) + 0.5*rho*(u*u+v*v+w*w);
}
}
}
if (!strcmp(ip_file_type,"ascii")) {
printf("Writing ASCII initial solution file initial.inp\n");
out = fopen("initial.inp","w");
for (i = 0; i < NI; i++) fprintf(out,"%1.16E ",x[i]);
fprintf(out,"\n");
for (j = 0; j < NJ; j++) fprintf(out,"%1.16E ",y[j]);
fprintf(out,"\n");
for (k = 0; k < NK; k++) fprintf(out,"%1.16E ",z[k]);
fprintf(out,"\n");
for (k = 0; k < NK; k++) {
for (j = 0; j < NJ; j++) {
for (i = 0; i < NI; i++) {
int p = i + NK*j + NI*NJ*k;
fprintf(out,"%1.16E ",U[5*p+0]);
}
}
}
fprintf(out,"\n");
for (k = 0; k < NK; k++) {
for (j = 0; j < NJ; j++) {
for (i = 0; i < NI; i++) {
int p = i + NK*j + NI*NJ*k;
fprintf(out,"%1.16E ",U[5*p+1]);
}
}
}
fprintf(out,"\n");
for (k = 0; k < NK; k++) {
for (j = 0; j < NJ; j++) {
for (i = 0; i < NI; i++) {
int p = i + NK*j + NI*NJ*k;
fprintf(out,"%1.16E ",U[5*p+2]);
}
}
}
fprintf(out,"\n");
for (k = 0; k < NK; k++) {
for (j = 0; j < NJ; j++) {
for (i = 0; i < NI; i++) {
int p = i + NK*j + NI*NJ*k;
fprintf(out,"%1.16E ",U[5*p+3]);
}
}
}
fprintf(out,"\n");
for (k = 0; k < NK; k++) {
for (j = 0; j < NJ; j++) {
for (i = 0; i < NI; i++) {
int p = i + NK*j + NI*NJ*k;
fprintf(out,"%1.16E ",U[5*p+4]);
}
}
}
fprintf(out,"\n");
fclose(out);
} else if ((!strcmp(ip_file_type,"binary")) || (!strcmp(ip_file_type,"bin"))) {
printf("Writing binary initial solution file initial.inp\n");
out = fopen("initial.inp","wb");
fwrite(x,sizeof(double),NI,out);
fwrite(y,sizeof(double),NJ,out);
fwrite(z,sizeof(double),NK,out);
fwrite(U,sizeof(double),5*NI*NJ*NK,out);
fclose(out);
}
free(x);
free(y);
free(z);
free(U);
return(0);
}
Output:
Note that iproc is set to
8 4 1
in solver.inp (i.e., 8 processors along x, 4 processors along y, and 1 processor along z). Thus, this example should be run with 32 MPI ranks (or change iproc).
Please see the original example in the "Immersed Boundaries Examples" section for a full description of the output files and how to view them. The following only contains libROM-specific comments.
After running the code, there should be the following output files:
- 1 output file op.bin; this is the predicted solutions from the DMD object(s).
The files is in binary format. (HyPar::op_file_format is set to binary in solver.inp).
The provided Python script (plotSolution.py) can be used to generate plots from the binary files. Alternatively, HyPar::op_file_format can be set to tecplot3d, and Tecplot/VisIt or something similar can be used to plot the resulting text files.
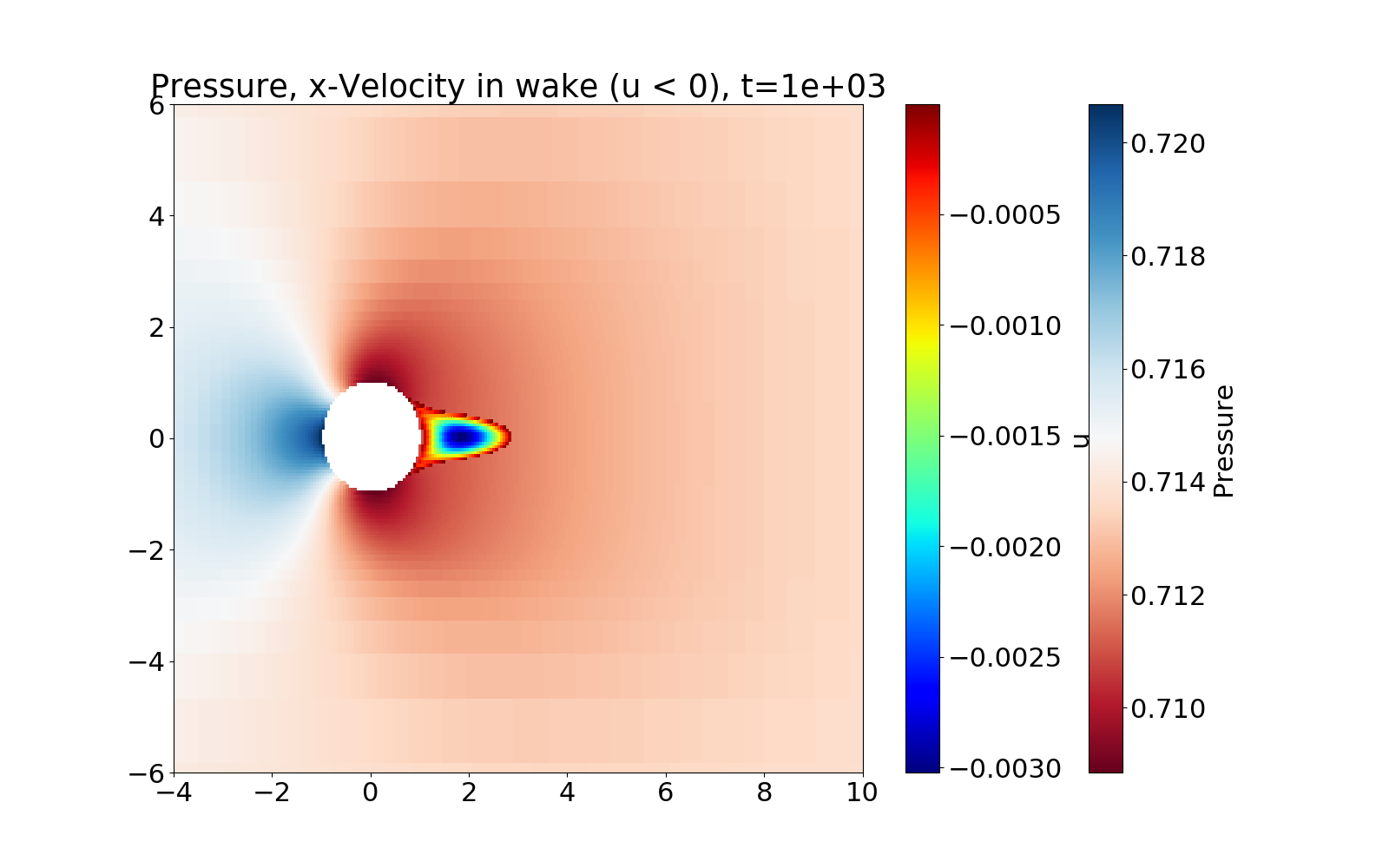
The following figure shows the flow at \(Re_D=20\). The pressure is plotted in the overall domain, and the wake is shown by plotting the x-velocity, where it is negative.
Expected screen output:
srun: job 9716416 queued and waiting for resources
srun: job 9716416 has been allocated resources
HyPar - Parallel (MPI) version with 32 processes
Compiled with PETSc time integration.
Allocated simulation object(s).
Reading solver inputs from file "solver.inp".
No. of dimensions : 3
No. of variables : 5
Domain size : 200 96 3
Processes along each dimension : 8 4 1
Exact solution domain size : 200 96 3
No. of ghosts pts : 3
No. of iter. : 1
Restart iteration : 0
Time integration scheme : euler
Spatial discretization scheme (hyperbolic) : 1
Split hyperbolic flux term? : no
Interpolation type for hyperbolic term : characteristic
Spatial discretization type (parabolic ) : nonconservative-2stage
Spatial discretization scheme (parabolic ) : 2
Time Step : 1.000000E+03
Check for conservation : no
Screen output iterations : 1
File output iterations : 1
Initial solution file type : binary
Initial solution read mode : serial
Solution file write mode : serial
Solution file format : binary
Overwrite solution file : yes
Physical model : navierstokes3d
Immersed Body : cylinder.stl
Partitioning domain and allocating data arrays.
Reading array from binary file initial.inp (Serial mode).
Volume integral of the initial solution:
0: 2.5654236261034112E+02
1: 2.5654236261034061E+01
2: 0.0000000000000000E+00
3: 0.0000000000000000E+00
4: 4.5939407361723192E+02
Reading boundary conditions from boundary.inp.
Boundary subsonic-inflow: Along dimension 0 and face +1
Boundary subsonic-outflow: Along dimension 0 and face -1
Boundary subsonic-ambivalent: Along dimension 1 and face +1
Boundary subsonic-ambivalent: Along dimension 1 and face -1
Boundary periodic: Along dimension 2 and face +1
Boundary periodic: Along dimension 2 and face -1
6 boundary condition(s) read.
Immersed body read from cylinder.stl:
Number of facets: 628
Bounding box: [-1.0,1.0] X [-1.0,1.0] X [-5.0,5.0]
Number of grid points inside immersed body: 3456 ( 6.0%).
Number of immersed boundary points : 882 ( 1.5%).
Immersed body simulation mode : 2d (xy).
Initializing solvers.
Initializing physics. Model = "navierstokes3d"
Reading physical model inputs from file "physics.inp".
Writing solution file iblank.bin.
Setting up libROM interface.
libROM inputs and parameters:
reduced model dimensionality: 0
sampling frequency: 0
mode: predict
type: DMD
save to file: true
libROM DMD inputs:
number of samples per window: 2147483647
directory name for DMD onjects: DMD
libROMInterface::loadROM() - loading ROM objects.
Loading DMD object (DMD/dmdobj_0000), time window=[0.00e+00,2.00e+02].
Loading DMD object (DMD/dmdobj_0001), time window=[2.00e+02,4.00e+02].
Loading DMD object (DMD/dmdobj_0002), time window=[4.00e+02,6.00e+02].
Loading DMD object (DMD/dmdobj_0003), time window=[6.00e+02,8.00e+02].
Loading DMD object (DMD/dmdobj_0004), time window=[8.00e+02,-1.00e+00].
libROM: Predicted solution at time 0.0000e+00 using ROM, wallclock time: 0.119344.
Writing immersed body surface data file surface.dat.
Writing solution file op.bin.
libROM: Predicted solution at time 1.0000e+03 using ROM, wallclock time: 0.140830.
Writing immersed body surface data file surface.dat.
Writing solution file op.bin.
libROM: total prediction/query wallclock time: 0.260174 (seconds).
Solver runtime (in seconds): 9.5630539999999993E+00
Total runtime (in seconds): 9.8863149999999997E+00
Deallocating arrays.
Finished.