3D Navier-Stokes Equations (with gravitational force) - Rising Thermal Bubble (Time-Windowed DMD) with PETSc IMEX time integration
See 3D Navier-Stokes Equations - Rising Thermal Bubble to familiarize yourself with this case.
Location: hypar/Examples/3D/NavierStokes3D/RisingThermalBubble_PETSc_IMEX_libROM_DMD_Train (This directory contains all the input files needed to run this case.)
Governing equations: 3D Navier-Stokes Equations (navierstokes3d.h)
Domain: \(0 \le x,y,z < 1000\,{\rm m}\), "slip-wall" (_SLIP_WALL_) boundaries everywhere, with zero wall velocity.
Reference:
- Kelly, J. F., Giraldo, F. X., "Continuous and discontinuous Galerkin methods for a scalable three-dimensional nonhydrostatic atmospheric model: Limited-area mode", J. Comput. Phys., 231, 2012, pp. 7988-8008 (see section 5.1.2).
- Giraldo, F. X., Kelly, J. F., Constantinescu, E. M., "Implicit-Explicit Formulations of a Three-Dimensional Nonhydrostatic Unified Model of the Atmosphere (NUMA)", SIAM J. Sci. Comput., 35 (5), 2013, pp. B1162-B1194 (see section 4.1).
The problem is solved here using implicit-explicit (IMEX) time integration, where the hyperbolic flux is partitioned into its entropy and acoustic components with the former integrated explicitly and the latter integrated implicitly. See the following reference:
- Ghosh, D., Constantinescu, E. M., "Semi-Implicit Time Integration of Atmospheric Flows with Characteristic-Based Flux Partitioning", SIAM Journal on Scientific Computing, 38 (3), 2016, A1848-A1875, http://dx.doi.org/10.1137/15M1044369.
Initial solution: A warm bubble in cool ambient atmosphere. Note that in this example, the gravitational forces and rising of the bubble is along the y-axis.
Other parameters (all dimensional quantities are in SI units):
- Specific heat ratio \(\gamma = 1.4\) (NavierStokes3D::gamma)
- Universal gas constant \(R = 287.058\) (NavierStokes3D::R)
- Gravitational force per unit mass \(g = 9.8\) along y-axis (NavierStokes3D::grav_y)
- Reference density (at zero altitude) \(\rho_{ref} = 1.1612055171196529\) (NavierStokes3D::rho0)
- Reference pressure (at zero altitude) \(P_{ref} = 100000\) (NavierStokes3D::p0)
- Hydrostatic balance type 2 (NavierStokes3D::HB)
Numerical Method:
- Spatial discretization (hyperbolic): 5th order WENO (Interp1PrimFifthOrderWENO())
- Time integration: PETSc (SolvePETSc())
- Method Class: Additive Runge-Kutta method (TSARKIMEX - https://petsc.org/release/docs/manualpages/TS/TSARKIMEX.html)
- Specific method: ARK 2e (TSARKIMEX2E - https://petsc.org/release/docs/manualpages/TS/TSARKIMEX2E.html)
Reduced Order Modeling:
- Mode: train (libROMInterface::m_mode, _ROM_MODE_TRAIN_)
- Component Mode: monolithic (libROMInterface::m_comp_mode, _ROM_COMP_MODE_MONOLITHIC_)
- Type: Dynamic Mode Decomposition (DMD) with time windowing (libROMInterface::m_rom_type)
- Latent subspace dimension: 16 (DMDROMObject::m_rdim)
- Sampling frequency: 1 (libROMInterface::m_sampling_freq)
- Number of samples per time window: 50 (DMDROMObject::m_num_window_samples)
Input files required:
.petscrc
# Use PETSc time-integration
-use-petscts
# Time integration scheme type - ARK
-ts_type arkimex
-ts_arkimex_type 2e
# Specify the terms to treat explicitly and implicitly
# In this example, the hyperbolic flux is partitioned
# into its entropy and acoustic components: f = [f-df] + [df]
# [f-df] - entropy component
# [df] - acoustic component
-hyperbolic_f_explicit # treat [f-df] explicitly
-hyperbolic_df_implicit # treat [df] implicitly
-source_implicit # treat source term implicitly
# thus, time step size is limited by the [f-df] term, i.e.,
# the flow velocity.
# no time-step adaptivity
-ts_adapt_type none
# For linear problens, tell nonlinear solver (SNES) to only use the linear solver (KSP)
-snes_type ksponly
# Linear solver (KSP) type
-ksp_type gmres
# Set relative tolerance
-ksp_rtol 1e-6
# Set absolute tolerance
-ksp_atol 1e-6
# use a preconditioner for solving the system
-with_pc
# preconditioner type - block Jacobi
-pc_type sor
-pc_sor_omega 1.0
-pc_sor_its 10
librom.inp
begin
rdim 16
sampling_frequency 1
mode train
dmd_num_win_samples 50
end
solver.inp
begin
ndims 3
nvars 5
size 64 64 64
iproc 4 4 4
ghost 3
n_iter 200
restart_iter 0
hyp_space_scheme weno5
hyp_flux_split yes
hyp_interp_type components
dt 2.0
conservation_check no
screen_op_iter 2
file_op_iter 20
ip_file_type binary
op_file_format binary
op_overwrite no
model navierstokes3d
end
boundary.inp
6
slip-wall 0 1 0 0 0 1000.0 0 1000.0
0.0 0.0 0.0
slip-wall 0 -1 0 0 0 1000.0 0 1000.0
0.0 0.0 0.0
slip-wall 1 1 0 1000.0 0 0 0 1000.0
0.0 0.0 0.0
slip-wall 1 -1 0 1000.0 0 0 0 1000.0
0.0 0.0 0.0
slip-wall 2 1 0 1000.0 0 1000.0 0 0
0.0 0.0 0.0
slip-wall 2 -1 0 1000.0 0 1000.0 0 0
0.0 0.0 0.0
physics.inp
begin
gamma 1.4
upwinding rusanov
gravity 0.0 9.8 0.0
rho_ref 1.1612055171196529
p_ref 100000.0
R 287.058
HB 2
end
weno.inp (optional)
begin
mapped 0
borges 0
yc 0
no_limiting 1
epsilon 0.000001
p 2.0
rc 0.3
xi 0.001
end
To generate initial.inp (initial solution), compile and run the following code in the run directory.
/*
This code generates the initial solution for the rising
thermal bubble case for the 3D Navier-Stokes equations.
Note: this code allocates the global domain, so be careful
when using it for a large number of grid points.
*/
#include <stdio.h>
#include <stdlib.h>
#include <math.h>
#include <string.h>
{
return(exp(a*log(x)));
}
int main()
{
double gamma = 1.4;
double R = 287.058;
double rho_ref = 1.1612055171196529;
double p_ref = 100000.0;
double grav_x = 0.0;
double grav_y = 9.8;
double grav_z = 0.0;
int HB = 0;
int NI,NJ,NK,ndims;
char ip_file_type[50]; strcpy(ip_file_type,"ascii");
FILE *in;
printf("Reading file \"solver.inp\"...\n");
in = fopen("solver.inp","r");
if (!in) {
printf("Error: Input file \"solver.inp\" not found.\n");
return(0);
} else {
char word[500];
fscanf(in,"%s",word);
if (!strcmp(word, "begin")) {
while (strcmp(word, "end")) {
fscanf(in,"%s",word);
if (!strcmp(word, "ndims")) fscanf(in,"%d",&ndims);
else if (!strcmp(word, "size")) {
fscanf(in,"%d",&NI);
fscanf(in,"%d",&NJ);
fscanf(in,"%d",&NK);
} else if (!strcmp(word, "ip_file_type")) fscanf(in,"%s",ip_file_type);
}
} else printf("Error: Illegal format in solver.inp. Crash and burn!\n");
}
fclose(in);
printf("Reading file \"physics.inp\"...\n");
in = fopen("physics.inp","r");
if (!in) {
printf("Error: Input file \"physics.inp\" not found.\n");
return(0);
} else {
char word[500];
fscanf(in,"%s",word);
if (!strcmp(word, "begin")) {
while (strcmp(word, "end")) {
fscanf(in,"%s",word);
if (!strcmp(word, "rho_ref")) fscanf(in,"%lf",&rho_ref);
else if (!strcmp(word, "p_ref" )) fscanf(in,"%lf",&p_ref );
else if (!strcmp(word, "gamma" )) fscanf(in,"%lf",&gamma );
else if (!strcmp(word, "R" )) fscanf(in,"%lf",&R );
else if (!strcmp(word, "HB" )) fscanf(in,"%d" ,&HB );
else if (!strcmp(word, "gravity")) {
fscanf(in,"%lf",&grav_x );
fscanf(in,"%lf",&grav_y );
fscanf(in,"%lf",&grav_z );
}
}
} else printf("Error: Illegal format in physics.inp. Crash and burn!\n");
}
fclose(in);
if (ndims != 3) {
printf("ndims is not 3 in solver.inp. this code is to generate 3D initial conditions\n");
return(0);
}
if (HB != 2) {
printf("Error: Specify \"HB\" as 2 in physics.inp.\n");
}
if ((grav_x != 0.0) || (grav_z != 0.0)) {
printf("Error: gravity must be zero along x and z for this example.\n");
return(0);
}
printf("Grid:\t\t\t%d X %d X %d\n",NI,NJ,NK);
printf("Reference density and pressure: %lf, %lf.\n",rho_ref,p_ref);
int i,j,k;
double dx = 1000.0 / ((double)(NI-1));
double dy = 1000.0 / ((double)(NJ-1));
double dz = 1000.0 / ((double)(NK-1));
double *x, *y, *z, *U;
x = (double*) calloc (NI , sizeof(double));
y = (double*) calloc (NJ , sizeof(double));
z = (double*) calloc (NK , sizeof(double));
U = (double*) calloc (5*NI*NJ*NK, sizeof(double));
/* Initial perturbation center */
double xc = 500;
double yc = 260;
double zc = 500;
double Cp = gamma * R / (gamma-1.0);
/* initial perturbation parameters */
double pi = 4.0*atan(1.0);
double rc = 250.0;
double T_ref = p_ref / (R * rho_ref);
for (i = 0; i < NI; i++){
for (j = 0; j < NJ; j++){
for (k = 0; k < NK; k++){
x[i] = i*dx;
y[j] = j*dy;
z[k] = k*dz;
int p = i + NI*j + NI*NJ*k;
/* temperature peturbation */
double r = sqrt((x[i]-xc)*(x[i]-xc)+(y[j]-yc)*(y[j]-yc)+(z[k]-zc)*(z[k]-zc));
double dtheta = (r>rc ? 0.0 : (0.5*(1.0+cos(pi*r/rc))) );
double theta = T_ref + dtheta;
double Pexner = 1.0 - (grav_y*y[j])/(Cp*T_ref);
double rho = (p_ref/(R*theta)) * raiseto(Pexner, (1.0/(gamma-1.0)));
double E = rho * (R/(gamma-1.0)) * theta*Pexner;
U[5*p+0] = rho;
U[5*p+1] = 0.0;
U[5*p+2] = 0.0;
U[5*p+3] = 0.0;
U[5*p+4] = E;
}
}
}
FILE *out;
if (!strcmp(ip_file_type,"ascii")) {
printf("Error: sorry, ASCII format initial solution file not implemented. ");
printf("Please choose \"ip_file_format\" in solver.inp as \"binary\".\n");
return(0);
} else if ((!strcmp(ip_file_type,"binary")) || (!strcmp(ip_file_type,"bin"))) {
printf("Writing binary initial solution file initial.inp\n");
out = fopen("initial.inp","wb");
fwrite(x,sizeof(double),NI,out);
fwrite(y,sizeof(double),NJ,out);
fwrite(z,sizeof(double),NK,out);
fwrite(U,sizeof(double),5*NI*NJ*NK,out);
fclose(out);
}
free(x);
free(y);
free(z);
free(U);
return(0);
}
Output:
Note that iproc is set to
4 4 4
in solver.inp (i.e., 4 processors along x, 4 processors along y, and 4 processor along z). Thus, this example should be run with 64 MPI ranks (or change iproc).
After running the code, there should be the following output files:
- 11 output file op_00000.bin, ..., op_00010.bin; this is the HyPar solutions.
- 11 output file op_rom_00000.bin, ..., op_rom_00010.bin; this is the predicted solutions from the DMD object(s).
All the files are binary (HyPar::op_file_format is set to binary in solver.inp).
The binary solution file contains the conserved variables ( \(\rho,\rho u,\rho v,\rho w,e\)).
The Python script plotSolution.py calculates the primitive and reference variables \(\rho,u,v,w,P,\theta,\rho_0,P_0,\pi,\theta_0\) (where the subscript \(0\) indicates the hydrostatic mean value) for both the op_* and op_rom_* files. It plots 3D figures for \(\theta\) (potential temperature) for the PDE solution, the DMD predictions, and the difference between the two.
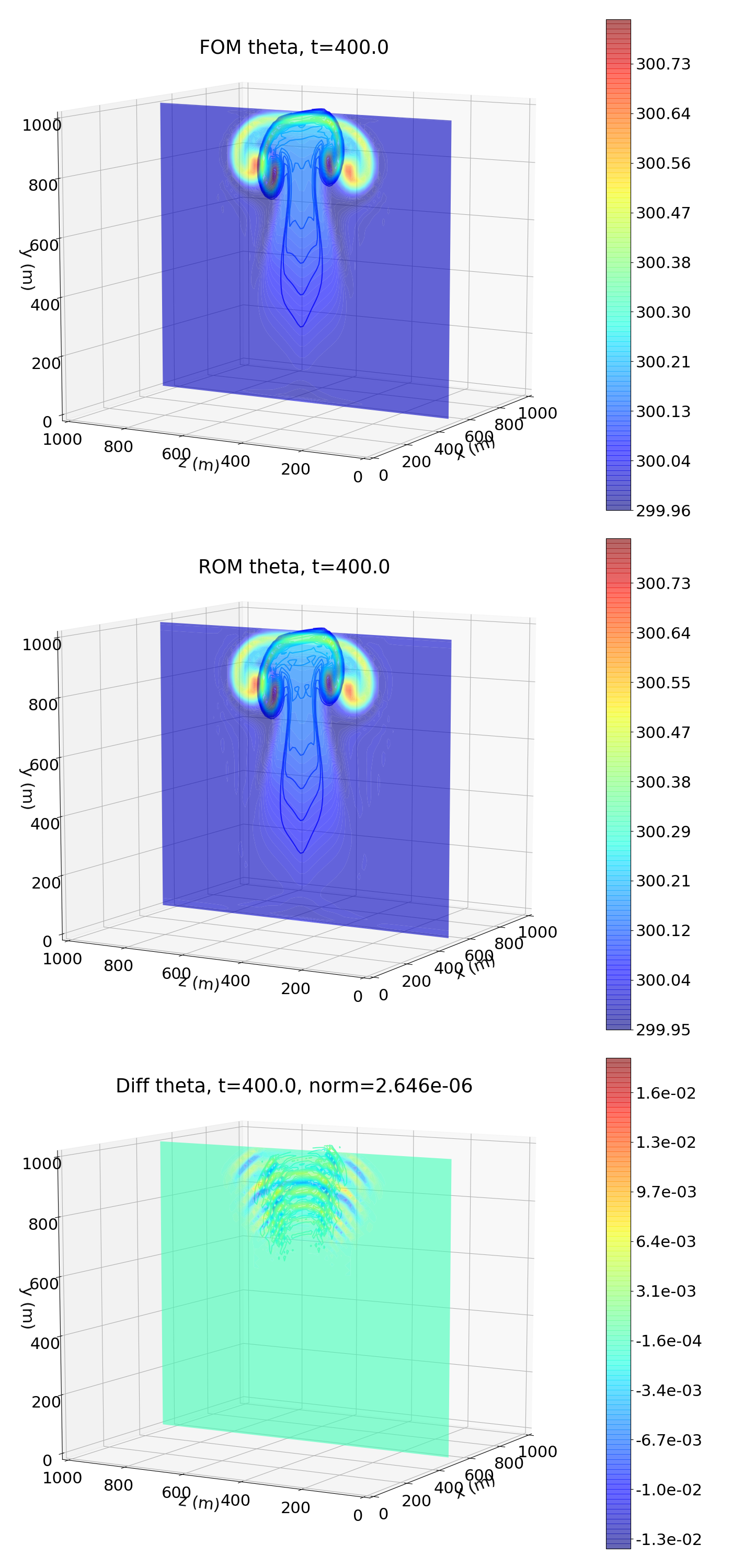
The following figure shows the potential temperature at the final time. Colored contours are plotted in the X-Y plane, and contour lines are plotted in the Z-Y plane (FOM is the HyPar solution, ROM is the DMD prediction, and diff is the difference between the two):
Wall clock times:
- PDE solution: 906 seconds
- DMD training time: 22.5 seconds
- DMD prediction/query time: 4.5 seconds
The L1, L2, and Linf norms of the diff between the HyPar and ROM solution at the final time are calculated and reported on screen (see below) as well as pde_rom_diff.dat:
64 64 64 4 4 4 2.0000000000000000E+00 3.5061348189940579E-09 8.1771689835182761E-09 1.8798434168943727E-07 9.3870696399999997E+02 9.3893929700000001E+02
The numbers are: number of grid points in each dimension (HyPar::dim_global), number of processors in each dimension (MPIVariables::iproc), time step size (HyPar::dt), L1, L2, and L-infinity norms of the diff (HyPar::rom_diff_norms), solver wall time (seconds) (i.e., not accounting for initialization, and cleaning up), and total wall time.
Expected screen output:
srun: job 10240594 queued and waiting for resources
srun: job 10240594 has been allocated resources
HyPar - Parallel (MPI) version with 64 processes
Compiled with PETSc time integration.
Allocated simulation object(s).
Reading solver inputs from file "solver.inp".
No. of dimensions : 3
No. of variables : 5
Domain size : 64 64 64
Processes along each dimension : 4 4 4
Exact solution domain size : 64 64 64
No. of ghosts pts : 3
No. of iter. : 200
Restart iteration : 0
Time integration scheme : PETSc
Spatial discretization scheme (hyperbolic) : weno5
Split hyperbolic flux term? : yes
Interpolation type for hyperbolic term : components
Spatial discretization type (parabolic ) : nonconservative-1stage
Spatial discretization scheme (parabolic ) : 2
Time Step : 2.000000E+00
Check for conservation : no
Screen output iterations : 2
File output iterations : 20
Initial solution file type : binary
Initial solution read mode : serial
Solution file write mode : serial
Solution file format : binary
Overwrite solution file : no
Physical model : navierstokes3d
Partitioning domain and allocating data arrays.
Reading array from binary file initial.inp (Serial mode).
Volume integral of the initial solution:
0: 1.1686650873135223E+09
1: 0.0000000000000000E+00
2: 0.0000000000000000E+00
3: 0.0000000000000000E+00
4: 2.4758406164981962E+14
Reading boundary conditions from boundary.inp.
Boundary slip-wall: Along dimension 0 and face +1
Boundary slip-wall: Along dimension 0 and face -1
Boundary slip-wall: Along dimension 1 and face +1
Boundary slip-wall: Along dimension 1 and face -1
Boundary slip-wall: Along dimension 2 and face +1
Boundary slip-wall: Along dimension 2 and face -1
6 boundary condition(s) read.
Initializing solvers.
Reading WENO parameters from weno.inp.
Initializing physics. Model = "navierstokes3d"
Reading physical model inputs from file "physics.inp".
Setting up PETSc time integration...
Setting up libROM interface.
libROMInterface inputs and parameters:
reduced model dimensionality: 16
sampling frequency: 1
mode: train
component mode: monolithic
type: DMD
save to file: true
DMDROMObject details:
number of samples per window: 50
directory name for DMD onjects: DMD
write snapshot matrix to file: false
simulation domain: 0
PETSc: total number of computational points is 262144.
PETSc: total number of computational DOFs is 1310720.
Implicit-Explicit time-integration:-
Hyperbolic (f-df) term: Explicit
Hyperbolic (df) term: Implicit
Parabolic term: Implicit
Source term: Implicit
SolvePETSc(): Problem type is linear.
** Starting PETSc time integration **
Writing solution file op_00000.bin.
DMDROMObject::takeSample() - creating new DMD object for sim. domain 0, var -1, t=0.000000 (total: 1).
iter= 2 dt=2.000E+00 t=4.000E+00 CFL=4.375E+01 norm=4.6613E-01 wctime: 3.7E+00 (s)
iter= 4 dt=2.000E+00 t=8.000E+00 CFL=4.375E+01 norm=1.7872E-01 wctime: 3.8E+00 (s)
iter= 6 dt=2.000E+00 t=1.200E+01 CFL=4.375E+01 norm=3.0277E-01 wctime: 3.8E+00 (s)
iter= 8 dt=2.000E+00 t=1.600E+01 CFL=4.376E+01 norm=4.0854E-01 wctime: 4.0E+00 (s)
iter= 10 dt=2.000E+00 t=2.000E+01 CFL=4.376E+01 norm=3.8615E-01 wctime: 3.8E+00 (s)
iter= 12 dt=2.000E+00 t=2.400E+01 CFL=4.376E+01 norm=2.7133E-01 wctime: 3.7E+00 (s)
iter= 14 dt=2.000E+00 t=2.800E+01 CFL=4.376E+01 norm=9.6926E-02 wctime: 4.0E+00 (s)
iter= 16 dt=2.000E+00 t=3.200E+01 CFL=4.376E+01 norm=7.2168E-02 wctime: 4.0E+00 (s)
iter= 18 dt=2.000E+00 t=3.600E+01 CFL=4.376E+01 norm=2.0010E-01 wctime: 4.2E+00 (s)
iter= 20 dt=2.000E+00 t=4.000E+01 CFL=4.376E+01 norm=2.5134E-01 wctime: 4.1E+00 (s)
Writing solution file op_00001.bin.
iter= 22 dt=2.000E+00 t=4.400E+01 CFL=4.377E+01 norm=2.3351E-01 wctime: 3.8E+00 (s)
iter= 24 dt=2.000E+00 t=4.800E+01 CFL=4.377E+01 norm=1.5111E-01 wctime: 3.8E+00 (s)
iter= 26 dt=2.000E+00 t=5.200E+01 CFL=4.378E+01 norm=4.7897E-02 wctime: 4.1E+00 (s)
iter= 28 dt=2.000E+00 t=5.600E+01 CFL=4.379E+01 norm=6.0644E-02 wctime: 4.1E+00 (s)
iter= 30 dt=2.000E+00 t=6.000E+01 CFL=4.379E+01 norm=1.2829E-01 wctime: 4.5E+00 (s)
iter= 32 dt=2.000E+00 t=6.400E+01 CFL=4.380E+01 norm=1.5991E-01 wctime: 4.1E+00 (s)
iter= 34 dt=2.000E+00 t=6.800E+01 CFL=4.381E+01 norm=1.3642E-01 wctime: 4.0E+00 (s)
iter= 36 dt=2.000E+00 t=7.200E+01 CFL=4.381E+01 norm=8.9307E-02 wctime: 4.0E+00 (s)
iter= 38 dt=2.000E+00 t=7.600E+01 CFL=4.382E+01 norm=1.9225E-02 wctime: 4.3E+00 (s)
iter= 40 dt=2.000E+00 t=8.000E+01 CFL=4.383E+01 norm=4.2010E-02 wctime: 4.3E+00 (s)
Writing solution file op_00002.bin.
iter= 42 dt=2.000E+00 t=8.400E+01 CFL=4.383E+01 norm=8.8311E-02 wctime: 4.4E+00 (s)
iter= 44 dt=2.000E+00 t=8.800E+01 CFL=4.384E+01 norm=9.5145E-02 wctime: 4.3E+00 (s)
iter= 46 dt=2.000E+00 t=9.200E+01 CFL=4.384E+01 norm=8.6380E-02 wctime: 4.2E+00 (s)
iter= 48 dt=2.000E+00 t=9.600E+01 CFL=4.385E+01 norm=4.6742E-02 wctime: 4.2E+00 (s)
iter= 50 dt=2.000E+00 t=1.000E+02 CFL=4.385E+01 norm=1.6582E-02 wctime: 4.4E+00 (s)
DMDROMObject::train() - training DMD object 0 for sim. domain 0, var -1 with 51 samples.
Using 16 basis vectors out of 50.
DMDROMObject::takeSample() - creating new DMD object for sim. domain 0, var -1, t=100.000000 (total: 2).
iter= 52 dt=2.000E+00 t=1.040E+02 CFL=4.386E+01 norm=3.7296E-02 wctime: 4.4E+00 (s)
iter= 54 dt=2.000E+00 t=1.080E+02 CFL=4.386E+01 norm=5.3518E-02 wctime: 4.5E+00 (s)
iter= 56 dt=2.000E+00 t=1.120E+02 CFL=4.387E+01 norm=6.5068E-02 wctime: 4.4E+00 (s)
iter= 58 dt=2.000E+00 t=1.160E+02 CFL=4.387E+01 norm=4.8353E-02 wctime: 4.4E+00 (s)
iter= 60 dt=2.000E+00 t=1.200E+02 CFL=4.388E+01 norm=3.4015E-02 wctime: 4.4E+00 (s)
Writing solution file op_00003.bin.
iter= 62 dt=2.000E+00 t=1.240E+02 CFL=4.388E+01 norm=1.8027E-02 wctime: 4.6E+00 (s)
iter= 64 dt=2.000E+00 t=1.280E+02 CFL=4.388E+01 norm=2.6413E-02 wctime: 4.6E+00 (s)
iter= 66 dt=2.000E+00 t=1.320E+02 CFL=4.388E+01 norm=4.2508E-02 wctime: 4.5E+00 (s)
iter= 68 dt=2.000E+00 t=1.360E+02 CFL=4.389E+01 norm=3.9334E-02 wctime: 4.6E+00 (s)
iter= 70 dt=2.000E+00 t=1.400E+02 CFL=4.389E+01 norm=3.7670E-02 wctime: 4.7E+00 (s)
iter= 72 dt=2.000E+00 t=1.440E+02 CFL=4.389E+01 norm=2.4546E-02 wctime: 4.6E+00 (s)
iter= 74 dt=2.000E+00 t=1.480E+02 CFL=4.389E+01 norm=2.2579E-02 wctime: 4.6E+00 (s)
iter= 76 dt=2.000E+00 t=1.520E+02 CFL=4.389E+01 norm=2.9157E-02 wctime: 4.6E+00 (s)
iter= 78 dt=2.000E+00 t=1.560E+02 CFL=4.389E+01 norm=3.1504E-02 wctime: 4.6E+00 (s)
iter= 80 dt=2.000E+00 t=1.600E+02 CFL=4.389E+01 norm=3.5025E-02 wctime: 4.6E+00 (s)
Writing solution file op_00004.bin.
iter= 82 dt=2.000E+00 t=1.640E+02 CFL=4.390E+01 norm=3.0110E-02 wctime: 4.6E+00 (s)
iter= 84 dt=2.000E+00 t=1.680E+02 CFL=4.390E+01 norm=2.8470E-02 wctime: 4.6E+00 (s)
iter= 86 dt=2.000E+00 t=1.720E+02 CFL=4.390E+01 norm=2.8242E-02 wctime: 4.5E+00 (s)
iter= 88 dt=2.000E+00 t=1.760E+02 CFL=4.390E+01 norm=3.0403E-02 wctime: 4.6E+00 (s)
iter= 90 dt=2.000E+00 t=1.800E+02 CFL=4.389E+01 norm=3.3249E-02 wctime: 4.6E+00 (s)
iter= 92 dt=2.000E+00 t=1.840E+02 CFL=4.389E+01 norm=3.3613E-02 wctime: 4.5E+00 (s)
iter= 94 dt=2.000E+00 t=1.880E+02 CFL=4.389E+01 norm=3.3177E-02 wctime: 4.5E+00 (s)
iter= 96 dt=2.000E+00 t=1.920E+02 CFL=4.389E+01 norm=3.3013E-02 wctime: 4.6E+00 (s)
iter= 98 dt=2.000E+00 t=1.960E+02 CFL=4.389E+01 norm=3.3826E-02 wctime: 4.5E+00 (s)
iter= 100 dt=2.000E+00 t=2.000E+02 CFL=4.389E+01 norm=3.5022E-02 wctime: 4.5E+00 (s)
Writing solution file op_00005.bin.
DMDROMObject::train() - training DMD object 1 for sim. domain 0, var -1 with 51 samples.
Using 16 basis vectors out of 50.
DMDROMObject::takeSample() - creating new DMD object for sim. domain 0, var -1, t=200.000000 (total: 3).
iter= 102 dt=2.000E+00 t=2.040E+02 CFL=4.389E+01 norm=3.7046E-02 wctime: 4.5E+00 (s)
iter= 104 dt=2.000E+00 t=2.080E+02 CFL=4.389E+01 norm=3.6900E-02 wctime: 4.5E+00 (s)
iter= 106 dt=2.000E+00 t=2.120E+02 CFL=4.389E+01 norm=3.8191E-02 wctime: 4.5E+00 (s)
iter= 108 dt=2.000E+00 t=2.160E+02 CFL=4.389E+01 norm=3.8205E-02 wctime: 4.6E+00 (s)
iter= 110 dt=2.000E+00 t=2.200E+02 CFL=4.388E+01 norm=3.9083E-02 wctime: 4.5E+00 (s)
iter= 112 dt=2.000E+00 t=2.240E+02 CFL=4.388E+01 norm=4.0808E-02 wctime: 4.5E+00 (s)
iter= 114 dt=2.000E+00 t=2.280E+02 CFL=4.388E+01 norm=4.0738E-02 wctime: 4.5E+00 (s)
iter= 116 dt=2.000E+00 t=2.320E+02 CFL=4.388E+01 norm=4.2765E-02 wctime: 4.5E+00 (s)
iter= 118 dt=2.000E+00 t=2.360E+02 CFL=4.388E+01 norm=4.2462E-02 wctime: 4.5E+00 (s)
iter= 120 dt=2.000E+00 t=2.400E+02 CFL=4.388E+01 norm=4.3767E-02 wctime: 4.5E+00 (s)
Writing solution file op_00006.bin.
iter= 122 dt=2.000E+00 t=2.440E+02 CFL=4.387E+01 norm=4.4773E-02 wctime: 4.5E+00 (s)
iter= 124 dt=2.000E+00 t=2.480E+02 CFL=4.387E+01 norm=4.5055E-02 wctime: 4.5E+00 (s)
iter= 126 dt=2.000E+00 t=2.520E+02 CFL=4.387E+01 norm=4.7022E-02 wctime: 4.5E+00 (s)
iter= 128 dt=2.000E+00 t=2.560E+02 CFL=4.387E+01 norm=4.6817E-02 wctime: 4.6E+00 (s)
iter= 130 dt=2.000E+00 t=2.600E+02 CFL=4.387E+01 norm=4.8519E-02 wctime: 4.6E+00 (s)
iter= 132 dt=2.000E+00 t=2.640E+02 CFL=4.387E+01 norm=4.9059E-02 wctime: 4.6E+00 (s)
iter= 134 dt=2.000E+00 t=2.680E+02 CFL=4.386E+01 norm=4.9884E-02 wctime: 4.6E+00 (s)
iter= 136 dt=2.000E+00 t=2.720E+02 CFL=4.386E+01 norm=5.1468E-02 wctime: 4.6E+00 (s)
iter= 138 dt=2.000E+00 t=2.760E+02 CFL=4.386E+01 norm=5.1688E-02 wctime: 4.6E+00 (s)
iter= 140 dt=2.000E+00 t=2.800E+02 CFL=4.386E+01 norm=5.3510E-02 wctime: 4.6E+00 (s)
Writing solution file op_00007.bin.
iter= 142 dt=2.000E+00 t=2.840E+02 CFL=4.386E+01 norm=5.4022E-02 wctime: 4.6E+00 (s)
iter= 144 dt=2.000E+00 t=2.880E+02 CFL=4.386E+01 norm=5.5372E-02 wctime: 4.6E+00 (s)
iter= 146 dt=2.000E+00 t=2.920E+02 CFL=4.386E+01 norm=5.6722E-02 wctime: 4.6E+00 (s)
iter= 148 dt=2.000E+00 t=2.960E+02 CFL=4.385E+01 norm=5.7594E-02 wctime: 4.7E+00 (s)
iter= 150 dt=2.000E+00 t=3.000E+02 CFL=4.385E+01 norm=5.9456E-02 wctime: 4.6E+00 (s)
DMDROMObject::train() - training DMD object 2 for sim. domain 0, var -1 with 51 samples.
Using 16 basis vectors out of 50.
DMDROMObject::takeSample() - creating new DMD object for sim. domain 0, var -1, t=300.000000 (total: 4).
iter= 152 dt=2.000E+00 t=3.040E+02 CFL=4.385E+01 norm=6.0386E-02 wctime: 4.6E+00 (s)
iter= 154 dt=2.000E+00 t=3.080E+02 CFL=4.385E+01 norm=6.2173E-02 wctime: 4.6E+00 (s)
iter= 156 dt=2.000E+00 t=3.120E+02 CFL=4.385E+01 norm=6.3620E-02 wctime: 4.6E+00 (s)
iter= 158 dt=2.000E+00 t=3.160E+02 CFL=4.385E+01 norm=6.5114E-02 wctime: 4.6E+00 (s)
iter= 160 dt=2.000E+00 t=3.200E+02 CFL=4.385E+01 norm=6.7011E-02 wctime: 4.6E+00 (s)
Writing solution file op_00008.bin.
iter= 162 dt=2.000E+00 t=3.240E+02 CFL=4.385E+01 norm=6.8407E-02 wctime: 4.6E+00 (s)
iter= 164 dt=2.000E+00 t=3.280E+02 CFL=4.384E+01 norm=7.0360E-02 wctime: 4.6E+00 (s)
iter= 166 dt=2.000E+00 t=3.320E+02 CFL=4.384E+01 norm=7.1921E-02 wctime: 4.6E+00 (s)
iter= 168 dt=2.000E+00 t=3.360E+02 CFL=4.384E+01 norm=7.3650E-02 wctime: 4.6E+00 (s)
iter= 170 dt=2.000E+00 t=3.400E+02 CFL=4.384E+01 norm=7.5378E-02 wctime: 4.6E+00 (s)
iter= 172 dt=2.000E+00 t=3.440E+02 CFL=4.384E+01 norm=7.6843E-02 wctime: 4.7E+00 (s)
iter= 174 dt=2.000E+00 t=3.480E+02 CFL=4.384E+01 norm=7.8483E-02 wctime: 4.6E+00 (s)
iter= 176 dt=2.000E+00 t=3.520E+02 CFL=4.384E+01 norm=7.9745E-02 wctime: 4.6E+00 (s)
iter= 178 dt=2.000E+00 t=3.560E+02 CFL=4.384E+01 norm=8.1031E-02 wctime: 4.6E+00 (s)
iter= 180 dt=2.000E+00 t=3.600E+02 CFL=4.383E+01 norm=8.2083E-02 wctime: 4.6E+00 (s)
Writing solution file op_00009.bin.
iter= 182 dt=2.000E+00 t=3.640E+02 CFL=4.383E+01 norm=8.2910E-02 wctime: 4.6E+00 (s)
iter= 184 dt=2.000E+00 t=3.680E+02 CFL=4.383E+01 norm=8.3637E-02 wctime: 4.6E+00 (s)
iter= 186 dt=2.000E+00 t=3.720E+02 CFL=4.383E+01 norm=8.4031E-02 wctime: 4.6E+00 (s)
iter= 188 dt=2.000E+00 t=3.760E+02 CFL=4.382E+01 norm=8.4328E-02 wctime: 4.6E+00 (s)
iter= 190 dt=2.000E+00 t=3.800E+02 CFL=4.382E+01 norm=8.4360E-02 wctime: 4.6E+00 (s)
iter= 192 dt=2.000E+00 t=3.840E+02 CFL=4.381E+01 norm=8.4218E-02 wctime: 4.6E+00 (s)
iter= 194 dt=2.000E+00 t=3.880E+02 CFL=4.381E+01 norm=8.3925E-02 wctime: 4.6E+00 (s)
iter= 196 dt=2.000E+00 t=3.920E+02 CFL=4.380E+01 norm=8.3438E-02 wctime: 4.7E+00 (s)
iter= 198 dt=2.000E+00 t=3.960E+02 CFL=4.380E+01 norm=8.2870E-02 wctime: 4.7E+00 (s)
iter= 200 dt=2.000E+00 t=4.000E+02 CFL=4.379E+01 norm=8.2161E-02 wctime: 4.7E+00 (s)
Writing solution file op_00010.bin.
** Completed PETSc time integration (Final time: 400.000000), total wctime: 906.731281 (seconds) **
DMDROMObject::train() - training DMD object 3 for sim. domain 0, var -1 with 50 samples.
Using 16 basis vectors out of 49.
libROM: total training wallclock time: 22.486292 (seconds).
libROM: Predicted solution at time 0.0000e+00 using ROM, wallclock time: 0.273265.
Writing solution file op_rom_00000.bin.
libROM: Predicted solution at time 4.0000e+01 using ROM, wallclock time: 0.410028.
Writing solution file op_rom_00001.bin.
libROM: Predicted solution at time 8.0000e+01 using ROM, wallclock time: 0.485338.
Writing solution file op_rom_00002.bin.
libROM: Predicted solution at time 1.2000e+02 using ROM, wallclock time: 0.379907.
Writing solution file op_rom_00003.bin.
libROM: Predicted solution at time 1.6000e+02 using ROM, wallclock time: 0.398802.
Writing solution file op_rom_00004.bin.
libROM: Predicted solution at time 2.0000e+02 using ROM, wallclock time: 0.383941.
Writing solution file op_rom_00005.bin.
libROM: Predicted solution at time 2.4000e+02 using ROM, wallclock time: 0.376884.
Writing solution file op_rom_00006.bin.
libROM: Predicted solution at time 2.8000e+02 using ROM, wallclock time: 0.383239.
Writing solution file op_rom_00007.bin.
libROM: Predicted solution at time 3.2000e+02 using ROM, wallclock time: 0.365753.
Writing solution file op_rom_00008.bin.
libROM: Predicted solution at time 3.6000e+02 using ROM, wallclock time: 0.365955.
Writing solution file op_rom_00009.bin.
libROM: Predicted solution at time 4.0000e+02 using ROM, wallclock time: 0.365799.
Writing solution file op_rom_00010.bin.
libROM: Predicted solution at time 4.0000e+02 using ROM, wallclock time: 0.365992.
libROM: Calculating diff between PDE and ROM solutions.
Writing solution file op_rom_00011.bin.
libROM: total prediction/query wallclock time: 4.554903 (seconds).
libROMInterface::saveROM() - saving ROM objects.
Saving DMD object and summary (DMD/dmdobj_0000, DMD/dmd_summary_0000).
Saving DMD object and summary (DMD/dmdobj_0001, DMD/dmd_summary_0001).
Saving DMD object and summary (DMD/dmdobj_0002, DMD/dmd_summary_0002).
Saving DMD object and summary (DMD/dmdobj_0003, DMD/dmd_summary_0003).
Norms of the diff between ROM and PDE solutions for domain 0:
L1 Norm : 3.5061348189940579E-09
L2 Norm : 8.1771689835182761E-09
Linfinity Norm : 1.8798434168943727E-07
Solver runtime (in seconds): 9.3870696399999997E+02
Total runtime (in seconds): 9.3893929700000001E+02
Deallocating arrays.
Finished.