3D Navier-Stokes Equations - Isotropic Turbulence Decay
See 3D Navier-Stokes Equations - Isotropic Turbulence Decay to familiarize yourself with this case.
Location: hypar/Examples/3D/NavierStokes3D/DNS_IsotropicTurbulenceDecay_CUDA (This directory contains all the input files needed to run this case.)
Governing equations: 3D Navier-Stokes Equations (navierstokes3d.h)
Domain: \(0 \le x,y,z < 2\pi\), "periodic" (_PERIODIC_) boundaries everywhere.
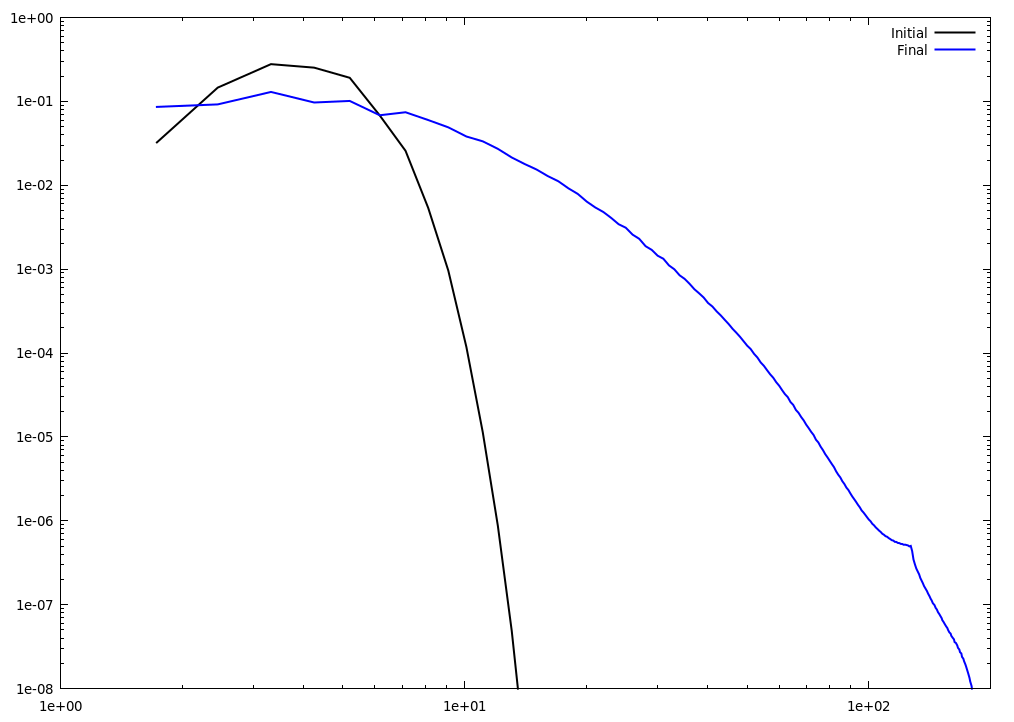
Initial solution: Isotropic turbulent flow - The initial solution is specified in the Fourier space (with an energy distribution similar to that of turbulent flow), and then transformed to the physical space through an inverse transform.
Other parameters:
- \(\gamma = 1.4\) (NavierStokes3D::gamma)
- \(Re = \frac {\rho u L } {\mu} = 333.33\) (NavierStokes3D::Re)
- \(Pr = 0.72\) (Prandtl number) (NavierStokes3D::Pr)
- \(M_\infty = 0.3\) (turbulence fluctuation Mach number) (NavierStokes3D::Minf)
Numerical Method:
- Spatial discretization (hyperbolic): 5th order CRWENO (Interp1PrimFifthOrderCRWENO())
- Spatial discretization (parabolic) : 4th order (FirstDerivativeFourthOrderCentral()) non-conservative 2-stage (ParabolicFunctionNC2Stage())
- Time integration: RK4 (TimeRK(), _RK_44_)
Hardware Details:
- GPU: NVIDIA V100 (Volta)
- CPU: IBM Power9
- Configuration: 16 nodes, 4 GPUs and 4 MPI ranks per node (64 GPUs and 64 MPI ranks).
Input files required:
solver.inp
begin
ndims 3
nvars 5
size 256 256 256
iproc 4 4 4
ghost 3
n_iter 1000
restart_iter 0
time_scheme rk
time_scheme_type ssprk3
hyp_space_scheme weno5
hyp_interp_type components
par_space_type nonconservative-2stage
par_space_scheme 4
dt 0.005
screen_op_iter 50
file_op_iter 100
ip_file_type binary
input_mode serial
op_file_format binary
op_overwrite no
model navierstokes3d
use_gpu yes
gpu_device_no 0
end
boundary.inp
6
periodic 0 1 0 0 0 6.3 0 6.3
periodic 0 -1 0 0 0 6.3 0 6.3
periodic 1 1 0 6.3 0 0 0 6.3
periodic 1 -1 0 6.3 0 0 0 6.3
periodic 2 1 0 6.3 0 6.3 0 0
periodic 2 -1 0 6.3 0 6.3 0 0
physics.inp
begin
gamma 1.4
upwinding roe
Pr 0.72
Minf 0.3
Re 333.333333333333333
end
weno.inp (optional)
begin
mapped 1
borges 0
yc 0
no_limiting 0
epsilon 0.000001
p 2.0
rc 0.3
xi 0.001
end
To generate initial.inp (initial solution), compile and run the following code in the run directory. Note: this code requires the FFTW library installed (http://www.fftw.org/). To compile:
gcc -I/path/to/fftw3.h -L/path/to/libfftw3.a -lfftw3 init.c
(see the FFTW website on ways to install it).
/*
This code generates the initial solution for the
isotropic turbulence decay problem, using the technique
described in the 1981 NASA report by Rogallo.
It needs the FFTW3 library installed. To compile it,
make sure the fftw3.h and libfftw3 are available in
the include and linking paths.
*/
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#include <math.h>
#include <fftw3.h>
static const double PI = 4 * atan(1.0);
return exp(a*log(x));
}
double magnitude(double a, double b) {
return sqrt(a*a + b*b);
}
void velocityComponent( const int N,
const int dir,
const double kp,
const double u0,
double* const uvel )
{
long N3 = N*N*N;
long i,j,k;
double kk = sqrt(3 * (N/2)*(N/2));
int kkmax = (int) kk;
fftw_complex *uhat = (fftw_complex*) fftw_malloc(N3 * sizeof(fftw_complex));
fftw_complex *u = (fftw_complex*) fftw_malloc(N3 * sizeof(fftw_complex));
fftw_plan inv_trans_u;
inv_trans_u = fftw_plan_dft_3d(N, N, N, uhat, u, 1, FFTW_MEASURE);
/* Specifying the velocities in Fourier space */
for (i=0; i<N3; i++) uhat[i][0] = uhat[i][1] = 0.0;
for (i = 1; i < N/2; i++){
for (j = 0; j < N/2; j++){
for (k = 0; k < N/2; k++){
double kk = sqrt(i*i + j*j + k*k);
double th1 = 2*PI * ((double)rand())/((double)RAND_MAX);
double th2 = 2*PI * ((double)rand())/((double)RAND_MAX);
double phi1 = 2*PI * ((double)rand())/((double)RAND_MAX);
double E = 16.0 * sqrt(2.0/PI) * (u0*u0/kp) * raiseto(kk/kp, 4.0)
* exp(-2.0*(kk/kp)*(kk/kp));
double alfa_real = sqrt(E/(4*PI*kk*kk))*cos(th1)*cos(phi1);
double alfa_imag = sqrt(E/(4*PI*kk*kk))*sin(th1)*cos(phi1);
double beta_real = sqrt(E/(4*PI*kk*kk))*cos(th2)*sin(phi1);
double beta_imag = sqrt(E/(4*PI*kk*kk))*sin(th2)*sin(phi1);
if (dir == 0) {
uhat[k+N*(j+N*i)][0] = (alfa_real*kk*j+beta_real*i*k)/(kk*sqrt(i*i+j*j));
uhat[k+N*(j+N*i)][1] = (alfa_imag*kk*j+beta_imag*i*k)/(kk*sqrt(i*i+j*j));
} else if (dir == 1) {
uhat[k+N*(j+N*i)][0] = (beta_real*j*k-alfa_real*kk*i)/(kk*sqrt(i*i+j*j));
uhat[k+N*(j+N*i)][1] = (beta_imag*j*k-alfa_imag*kk*i)/(kk*sqrt(i*i+j*j));
} else {
uhat[k+N*(j+N*i)][0] = -(beta_real*sqrt(i*i+j*j))/kk;
uhat[k+N*(j+N*i)][1] = -(beta_imag*sqrt(i*i+j*j))/kk;
}
}
}
}
for (i = 0; i < 1; i++){
for (k = 0; k < N/2; k++){
for (j = 1; j < N/2; j++){
double kk = sqrt(i*i + j*j + k*k);
double th1 = 2*PI * ((double)rand())/((double)RAND_MAX);
double th2 = 2*PI * ((double)rand())/((double)RAND_MAX);
double phi1 = 2*PI * ((double)rand())/((double)RAND_MAX);
double E = 16.0 * sqrt(2.0/PI) * (u0*u0/kp) * raiseto(kk/kp, 4.0)
* exp(-2.0*(kk/kp)*(kk/kp));
double alfa_real = sqrt(E/(4*PI*kk*kk))*cos(th1)*cos(phi1);
double alfa_imag = sqrt(E/(4*PI*kk*kk))*sin(th1)*cos(phi1);
double beta_real = sqrt(E/(4*PI*kk*kk))*cos(th2)*sin(phi1);
double beta_imag = sqrt(E/(4*PI*kk*kk))*sin(th2)*sin(phi1);
if (dir == 0) {
uhat[k+N*(j+N*i)][0] = (alfa_real*kk*j+beta_real*i*k)/(kk*sqrt(i*i+j*j));
uhat[k+N*(j+N*i)][1] = (alfa_imag*kk*j+beta_imag*i*k)/(kk*sqrt(i*i+j*j));
} else if (dir == 1) {
uhat[k+N*(j+N*i)][0] = (beta_real*j*k-alfa_real*kk*i)/(kk*sqrt(i*i+j*j));
uhat[k+N*(j+N*i)][1] = (beta_imag*j*k-alfa_imag*kk*i)/(kk*sqrt(i*i+j*j));
} else {
uhat[k+N*(j+N*i)][0] = -(beta_real*sqrt(i*i+j*j))/kk;
uhat[k+N*(j+N*i)][1] = -(beta_imag*sqrt(i*i+j*j))/kk;
}
}
}
}
for (i = 0; i < 1; i++){
for (j = 0; j < 1; j++){
for (k = 0; k < N/2; k++){
uhat[k+N*(j+N*i)][0] = 0;
uhat[k+N*(j+N*i)][1] = 0;
}
}
}
/* The following is necessary to ensure that the inverse Fourier
transform yields a real velocity field with zero imaginary
components */
for (i=N/2+1; i<N; i++) {
for (j=N/2+1; j<N; j++) {
for (k=N/2+1; k<N; k++) {
uhat[k+N*(j+N*i)][0] = uhat[(N-k)+N*((N-j)+N*(N-i))][0];
uhat[k+N*(j+N*i)][1] = -uhat[(N-k)+N*((N-j)+N*(N-i))][1];
}
}
}
for (i=N/2+1; i<N; i++) {
for (j=N/2+1; j<N; j++) {
for (k=0; k<1; k++) {
uhat[k+N*(j+N*i)][0] = uhat[k+N*((N-j)+N*(N-i))][0];
uhat[k+N*(j+N*i)][1] = -uhat[k+N*((N-j)+N*(N-i))][1];
}
}
}
for (i=N/2+1; i<N; i++) {
for (j=0; j<1; j++) {
for (k=N/2+1; k<N; k++) {
uhat[k+N*(j+N*i)][0] = uhat[(N-k)+N*(j+N*(N-i))][0];
uhat[k+N*(j+N*i)][1] = -uhat[(N-k)+N*(j+N*(N-i))][1];
}
}
}
for (i=0; i<1; i++) {
for (j=N/2+1; j<N; j++) {
for (k=N/2+1; k<N; k++) {
uhat[k+N*(j+N*i)][0] = uhat[(N-k)+N*((N-j)+N*i)][0];
uhat[k+N*(j+N*i)][1] = -uhat[(N-k)+N*((N-j)+N*i)][1];
}
}
}
for (i=0; i<1; i++) {
for (j=0; j<1; j++) {
for (k=N/2+1; k<N; k++) {
uhat[k+N*(j+N*i)][0] = uhat[(N-k)+N*(j+N*i)][0];
uhat[k+N*(j+N*i)][1] = -uhat[(N-k)+N*(j+N*i)][1];
}
}
}
for (i=0; i<1; i++) {
for (j=N/2+1; j<N; j++) {
for (k=0; k<1; k++) {
uhat[k+N*(j+N*i)][0] = uhat[k+N*((N-j)+N*i)][0];
uhat[k+N*(j+N*i)][1] = -uhat[k+N*((N-j)+N*i)][1];
}
}
}
for (i=N/2+1; i<N; i++) {
for (j=0; j<1; j++) {
for (k=0; k<1; k++) {
uhat[k+N*(j+N*i)][0] = uhat[k+N*(j+N*(N-i))][0];
uhat[k+N*(j+N*i)][1] = -uhat[k+N*(j+N*(N-i))][1];
}
}
}
/* Inverse Fourier transform */
fftw_execute(inv_trans_u);
fftw_free(uhat);
fftw_destroy_plan(inv_trans_u);
double imag_velocity = 0;
for (i = 0; i < N3; i++){
double uu = u[i][1];
imag_velocity += (uu*uu);
}
imag_velocity = sqrt(imag_velocity / ((double)N3));
printf("RMS of imaginary component of computed velocity: %1.6e\n",imag_velocity);
for (i = 0; i < N3; i++){
uvel[i] = u[i][0];
}
fftw_free(u);
return;
}
void setVelocityField(const int N,
double* const uvel,
double* const vvel,
double* const wvel )
{
double kp = 4.0;
double u0 = 0.3;
long N3 = N*N*N;
long i,j,k;
double dx = 2*PI / ((double)N);
velocityComponent( N, 0, kp, u0, uvel );
velocityComponent( N, 1, kp, u0, vvel );
velocityComponent( N, 2, kp, u0, wvel );
double rms_velocity = 0;
for (i = 0; i < N3; i++){
double uu, vv, ww;
uu = uvel[i];
vv = vvel[i];
ww = wvel[i];
rms_velocity += (uu*uu + vv*vv + ww*ww);
}
rms_velocity = sqrt(rms_velocity / (3*((double)N3)));
/* scale the velocity components so that rms velocity matches u0 */
double factor = u0 / rms_velocity;
printf("Scaling factor = %1.16E\n",factor);
for (i = 0; i < N3; i++){
uvel[i] *= factor;
vvel[i] *= factor;
wvel[i] *= factor;
}
rms_velocity = 0;
for (i = 0; i < N3; i++){
double uu, vv, ww;
uu = uvel[i];
vv = vvel[i];
ww = wvel[i];
rms_velocity += (uu*uu + vv*vv + ww*ww);
}
rms_velocity = sqrt(rms_velocity / (3*((double)N3)));
printf("RMS velocity (component-wise): %1.16E\n",rms_velocity);
/* calculate the divergence of velocity */
double DivergenceNorm = 0;
for (i=0; i<N; i++) {
for (j=0; j<N; j++) {
for (k=0; k<N; k++) {
double u1, u2, v1, v2, w1, w2;
u1 = (i==0 ? uvel[k+N*(j+N*(N-1))] : uvel[k+N*(j+N*(i-1))] );
u2 = (i==N-1 ? uvel[k+N*(j+N*(0 ))] : uvel[k+N*(j+N*(i+1))] );
v1 = (j==0 ? vvel[k+N*((N-1)+N*i)] : vvel[k+N*((j-1)+N*i)] );
v2 = (j==N-1 ? vvel[k+N*((0 )+N*i)] : vvel[k+N*((j+1)+N*i)] );
w1 = (k==0 ? wvel[(N-1)+N*(j+N*i)] : wvel[(k-1)+N*(j+N*i)] );
w2 = (k==N-1 ? wvel[(0 )+N*(j+N*i)] : wvel[(k+1)+N*(j+N*i)] );
double Divergence = ( (u2-u1) + (v2-v1) + (w2-w1) ) / (2.0*dx);
DivergenceNorm += (Divergence*Divergence);
}
}
}
DivergenceNorm = sqrt(DivergenceNorm / ((double)N3));
printf("Velocity divergence: %1.16E\n",DivergenceNorm);
/* calculate the Taylor microscales */
double TaylorMicroscale[3];
double Numerator[3] = {0,0,0};
double Denominator[3] = {0,0,0};
for (i=0; i<N; i++) {
for (j=0; j<N; j++) {
for (k=0; k<N; k++) {
double u1, u2, uu, v1, v2, vv, w1, w2, ww;
u1 = (i==0 ? uvel[k+N*(j+N*(N-1))] : uvel[k+N*(j+N*(i-1))] );
u2 = (i==N-1 ? uvel[k+N*(j+N*(0 ))] : uvel[k+N*(j+N*(i+1))] );
v1 = (j==0 ? vvel[k+N*((N-1)+N*i)] : vvel[k+N*((j-1)+N*i)] );
v2 = (j==N-1 ? vvel[k+N*((0 )+N*i)] : vvel[k+N*((j+1)+N*i)] );
w1 = (k==0 ? wvel[(N-1)+N*(j+N*i)] : wvel[(k-1)+N*(j+N*i)] );
w2 = (k==N-1 ? wvel[(0 )+N*(j+N*i)] : wvel[(k+1)+N*(j+N*i)] );
uu = uvel[k+N*(j+N*i)];
vv = vvel[k+N*(j+N*i)];
ww = wvel[k+N*(j+N*i)];
double du, dv, dw;
du = (u2 - u1) / (2.0*dx);
dv = (v2 - v1) / (2.0*dx);
dw = (w2 - w1) / (2.0*dx);
Numerator[0] += (uu*uu);
Numerator[1] += (vv*vv);
Numerator[2] += (ww*ww);
Denominator[0] += (du*du);
Denominator[1] += (dv*dv);
Denominator[2] += (dw*dw);
}
}
}
Numerator[0] /= (N*N*N); Denominator[0] /= (N*N*N);
Numerator[1] /= (N*N*N); Denominator[1] /= (N*N*N);
Numerator[2] /= (N*N*N); Denominator[2] /= (N*N*N);
TaylorMicroscale[0] = sqrt(Numerator[0]/Denominator[0]);
TaylorMicroscale[1] = sqrt(Numerator[1]/Denominator[1]);
TaylorMicroscale[2] = sqrt(Numerator[2]/Denominator[2]);
printf("Taylor microscales: %1.16E, %1.16E, %1.16E\n",
TaylorMicroscale[0],TaylorMicroscale[1],TaylorMicroscale[2]);
return;
}
int main()
{
FILE *out, *in;
int NI,NJ,NK,ndims;
char ip_file_type[50];
strcpy(ip_file_type,"ascii");
printf("Reading file \"solver.inp\"...\n");
in = fopen("solver.inp","r");
if (!in) printf("Error: Input file \"solver.inp\" not found. Default values will be used.\n");
else {
char word[500];
fscanf(in,"%s",word);
if (!strcmp(word, "begin")){
while (strcmp(word, "end")){
fscanf(in,"%s",word);
if (!strcmp(word, "ndims")) fscanf(in,"%d",&ndims);
else if (!strcmp(word, "size")) {
fscanf(in,"%d",&NI);
fscanf(in,"%d",&NJ);
fscanf(in,"%d",&NK);
} else if (!strcmp(word, "ip_file_type")) fscanf(in,"%s",ip_file_type);
}
} else printf("Error: Illegal format in solver.inp. Crash and burn!\n");
}
fclose(in);
if (ndims != 3) {
printf("ndims is not 3 in solver.inp. this code is to generate 3D exact conditions\n");
return(0);
}
printf("Grid:\t\t\t%d x %d x %d\n",NI,NJ,NK);
if ((NI != NJ) || (NI != NK) || (NJ != NK)) {
printf("Error: NI,NJ,NK not equal. Bye!\n");
return(0);
}
int N = NI;
long N3 = N*N*N;
int i,j,k;
double dx = 2*PI / ((double)N);
/* Calculating the velocity components through a Fourier transform */
double* u = (double*) calloc (N3, sizeof(double));
double* v = (double*) calloc (N3, sizeof(double));
double* w = (double*) calloc (N3, sizeof(double));
setVelocityField(N, u, v, w);
/* grid and solution in conserved variable form */
double *x,*y,*z,*U;
x = (double*) calloc (N, sizeof(double));
y = (double*) calloc (N, sizeof(double));
z = (double*) calloc (N, sizeof(double));
U = (double*) calloc (5*N3, sizeof(double));
for (i = 0; i < N; i++){
for (j = 0; j < N; j++){
for (k = 0; k < N; k++){
x[i] = i*dx;
y[j] = j*dx;
z[k] = k*dx;
double RHO, uvel, vvel, wvel, P;
RHO = 1.0;
uvel = u[k+N*(j+N*i)];
vvel = v[k+N*(j+N*i)];
wvel = w[k+N*(j+N*i)];
P = 1.0/1.4;
long p = i + N*j + N*N*k;
U[5*p+0] = RHO;
U[5*p+1] = RHO*uvel;
U[5*p+2] = RHO*vvel;
U[5*p+3] = RHO*wvel;
U[5*p+4] = P/0.4 + 0.5 * RHO * (uvel*uvel + vvel*vvel + wvel*wvel);
}
}
}
free(u);
free(v);
free(w);
FILE *op;
if (!strcmp(ip_file_type,"ascii")) {
printf("Writing ASCII initial solution file initial.inp\n");
op = fopen("initial.inp","w");
for (i = 0; i < N; i++) fprintf(op,"%1.16E ",x[i]);
fprintf(op,"\n");
for (j = 0; j < N; j++) fprintf(op,"%1.16E ",y[j]);
fprintf(op,"\n");
for (k = 0; k < N; k++) fprintf(op,"%1.16E ",z[k]);
fprintf(op,"\n");
for (i = 0; i < N; i++) {
for (j = 0; j < N; j++) {
for (k = 0; k < N; k++) {
int p = i + N*j + N*N*k;
fprintf(op,"%1.16E ",U[5*p+0]);
}
}
}
fprintf(op,"\n");
for (i = 0; i < N; i++) {
for (j = 0; j < N; j++) {
for (k = 0; k < N; k++) {
int p = i + N*j + N*N*k;
fprintf(op,"%1.16E ",U[5*p+1]);
}
}
}
fprintf(op,"\n");
for (i = 0; i < N; i++) {
for (j = 0; j < N; j++) {
for (k = 0; k < N; k++) {
int p = i + N*j + N*N*k;
fprintf(op,"%1.16E ",U[5*p+2]);
}
}
}
fprintf(op,"\n");
for (i = 0; i < N; i++) {
for (j = 0; j < N; j++) {
for (k = 0; k < N; k++) {
int p = i + N*j + N*N*k;
fprintf(op,"%1.16E ",U[5*p+3]);
}
}
}
fprintf(op,"\n");
for (i = 0; i < N; i++) {
for (j = 0; j < N; j++) {
for (k = 0; k < N; k++) {
int p = i + N*j + N*N*k;
fprintf(op,"%1.16E ",U[5*p+4]);
}
}
}
fprintf(op,"\n");
fclose(op);
} else if ((!strcmp(ip_file_type,"binary")) || (!strcmp(ip_file_type,"bin"))) {
printf("Writing binary initial solution file initial.inp\n");
op = fopen("initial.inp","wb");
fwrite(x,sizeof(double),N,op);
fwrite(y,sizeof(double),N,op);
fwrite(z,sizeof(double),N,op);
fwrite(U,sizeof(double),5*N3,op);
fclose(op);
}
free(x);
free(y);
free(z);
free(U);
return(0);
}
Output:
Note that iproc is set to
4 4 4
in solver.inp (i.e., 4 processors along x, 4 processors along y, and 4 processor along z). Thus, this example should be run with 64 MPI ranks (or change iproc) and 64 GPUs.
After running the code, there should be 11 output files op_00000.bin, op_00001.bin, ... op_00010.bin; the first one is the solution at \(t=0\) and the final one is the solution at \(t=5\).
See 3D Navier-Stokes Equations - Isotropic Turbulence Decay for detailed postprocessing instructions. The following figure shows the initial and final (t=5) energy spectra:
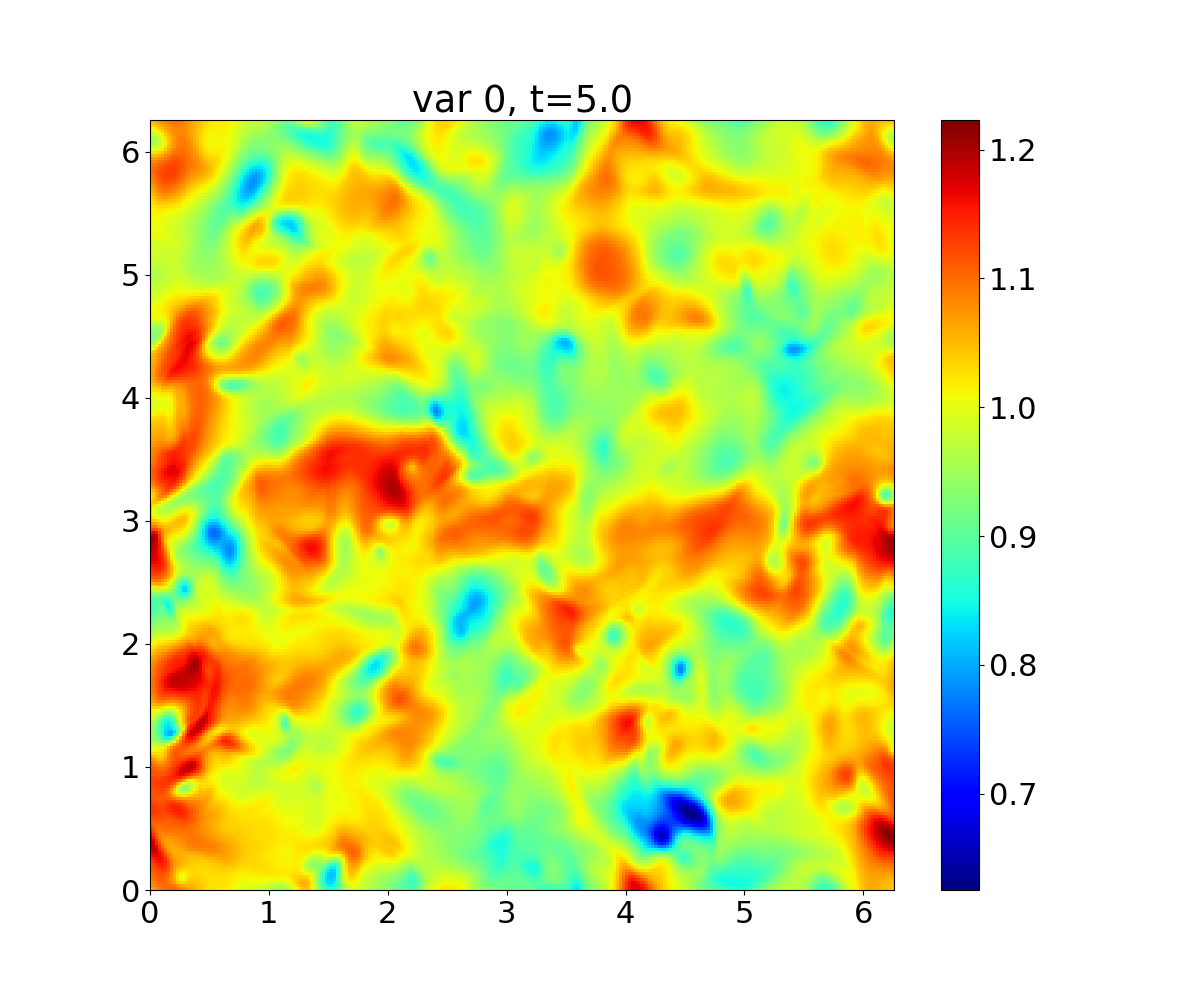
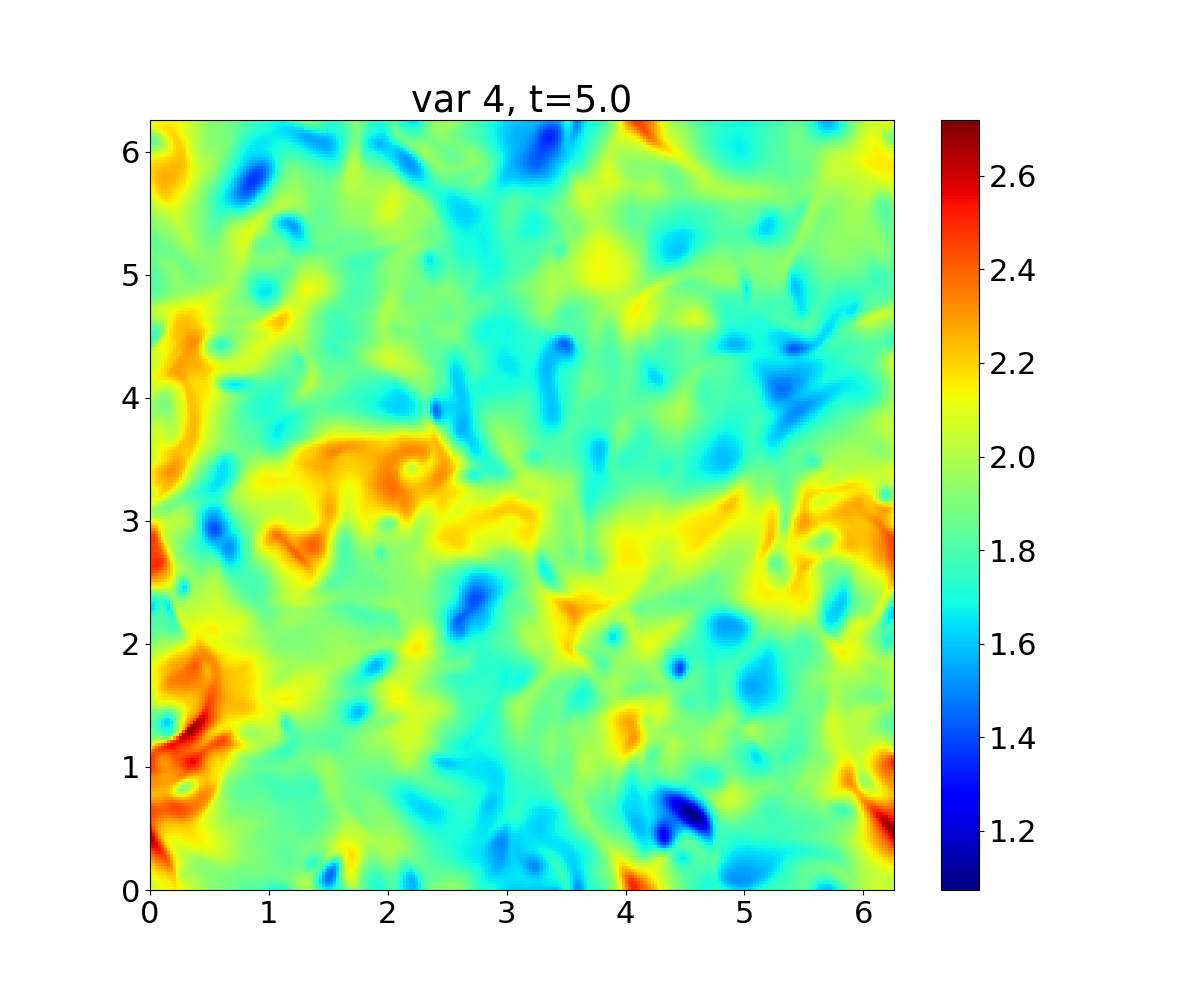
The following figures show the density and internal energy contours on the X-Y plane mid-slice at the final time:
Expected screen output:
HyPar - Parallel (MPI) version with 64 processes
Allocated simulation object(s).
Reading solver inputs from file "solver.inp".
No. of dimensions : 3
No. of variables : 5
Domain size : 256 256 256
Processes along each dimension : 4 4 4
Exact solution domain size : 256 256 256
No. of ghosts pts : 3
No. of iter. : 1000
Restart iteration : 0
Time integration scheme : rk (ssprk3)
Spatial discretization scheme (hyperbolic) : weno5
Split hyperbolic flux term? : no
Interpolation type for hyperbolic term : components
Spatial discretization type (parabolic ) : nonconservative-2stage
Spatial discretization scheme (parabolic ) : 4
Time Step : 5.000000E-03
Check for conservation : no
Screen output iterations : 50
File output iterations : 100
Initial solution file type : binary
Initial solution read mode : serial
Solution file write mode : serial
Solution file format : binary
Overwrite solution file : no
Use GPU : yes
GPU device no : 0
Physical model : navierstokes3d
Partitioning domain and allocating data arrays.
Reading array from binary file initial.inp (Serial mode).
Volume integral of the initial solution:
0: 2.4805021344162057E+02
1: 3.6748382115092681E-14
2: 5.6732396558345499E-14
3: 3.9412917374193057E-14
4: 4.7643358853329369E+02
Reading boundary conditions from boundary.inp.
Boundary periodic: Along dimension 0 and face +1
Boundary periodic: Along dimension 0 and face -1
Boundary periodic: Along dimension 1 and face +1
Boundary periodic: Along dimension 1 and face -1
Boundary periodic: Along dimension 2 and face +1
Boundary periodic: Along dimension 2 and face -1
6 boundary condition(s) read.
Initializing solvers.
Reading WENO parameters from weno.inp.
Initializing physics. Model = "navierstokes3d"
Reading physical model inputs from file "physics.inp".
Setting up time integration.
Solving in time (from 0 to 1000 iterations)
Writing solution file op_00000.bin.
iter= 50 t=2.500E-01 wctime: 8.3E-02 (s)
iter= 100 t=5.000E-01 wctime: 8.2E-02 (s)
Writing solution file op_00001.bin.
iter= 150 t=7.500E-01 wctime: 8.2E-02 (s)
iter= 200 t=1.000E+00 wctime: 8.3E-02 (s)
Writing solution file op_00002.bin.
iter= 250 t=1.250E+00 wctime: 8.3E-02 (s)
iter= 300 t=1.500E+00 wctime: 8.3E-02 (s)
Writing solution file op_00003.bin.
iter= 350 t=1.750E+00 wctime: 8.2E-02 (s)
iter= 400 t=2.000E+00 wctime: 8.2E-02 (s)
Writing solution file op_00004.bin.
iter= 450 t=2.250E+00 wctime: 8.2E-02 (s)
iter= 500 t=2.500E+00 wctime: 8.2E-02 (s)
Writing solution file op_00005.bin.
iter= 550 t=2.750E+00 wctime: 8.3E-02 (s)
iter= 600 t=3.000E+00 wctime: 8.2E-02 (s)
Writing solution file op_00006.bin.
iter= 650 t=3.250E+00 wctime: 8.2E-02 (s)
iter= 700 t=3.500E+00 wctime: 8.3E-02 (s)
Writing solution file op_00007.bin.
iter= 750 t=3.750E+00 wctime: 8.3E-02 (s)
iter= 800 t=4.000E+00 wctime: 8.3E-02 (s)
Writing solution file op_00008.bin.
iter= 850 t=4.250E+00 wctime: 8.2E-02 (s)
iter= 900 t=4.500E+00 wctime: 8.2E-02 (s)
Writing solution file op_00009.bin.
iter= 950 t=4.750E+00 wctime: 8.3E-02 (s)
iter= 1000 t=5.000E+00 wctime: 8.2E-02 (s)
Completed time integration (Final time: 5.000000), total wctime: 82.421372 (seconds).
Writing solution file op_00010.bin.
Solver runtime (in seconds): 9.5411868999999996E+01
Total runtime (in seconds): 1.0222746800000000E+02
Deallocating arrays.
Finished.