Interp2PrimSecondOrder.c File Reference

2nd order interpolation of the 2nd primitive More...

#include <stdio.h>
#include <stdlib.h>
#include <basic.h>
#include <arrayfunctions.h>
#include <interpolation.h>
#include <mpivars.h>
#include <hypar.h>

Go to the source code of this file.

Macros
#define	_MINIMUM_GHOSTS_   1

Functions
int	Interp2PrimSecondOrder (double *fI, double *fC, int dir, void *s, void *m)
	2nd order component-wise interpolation of the 2nd primitive on a uniform grid More...

Detailed Description

2nd order interpolation of the 2nd primitive

Author

Debojyoti Ghosh

Definition in file Interp2PrimSecondOrder.c.

Macro Definition Documentation

_MINIMUM_GHOSTS_

#define _MINIMUM_GHOSTS_   1

Minimum number of ghost points required for this interpolation method.

Definition at line 19 of file Interp2PrimSecondOrder.c.

Function Documentation

Interp2PrimSecondOrder()

int Interp2PrimSecondOrder	(	double *	fI,
		double *	fC,
		int	dir,
		void *	s,
		void *	m
	)

2nd order component-wise interpolation of the 2nd primitive on a uniform grid

Computes the interpolated values of the second primitive of a function \({\bf f}\left({\bf u}\right)\) at the interfaces from the cell-centered values of the function using the second order central method on a uniform grid. The second primitive is defined as a function \({\bf h}\left({\bf u}\right)\) that satisfies:

\begin{equation} {\bf f}\left({\bf u}\left(x\right)\right) = \frac{1}{\Delta x^2} \int_{x-\Delta x/2}^{x+\Delta x/2} \left( \int_{\eta-\Delta x/2}^{\eta+\Delta x/2} {\bf h}\left({\bf u}\left(\zeta\right)\right) d\zeta \right) d\eta, \end{equation}

where \(x\) is the spatial coordinate along the dimension of the interpolation. This function the 2nd order central numerical approximation \(\hat{\bf f}_{j+1/2} \approx {\bf h}_{j+1/2}\) as \(\hat{\bf f}_{j+1/2} \approx {\bf h}_{j+1/2}\) as:

\begin{equation} \hat{\bf f}_{j+1/2} = \frac{1}{2}\left( {\bf f}_{j+1} - {\bf f}_j \right). \end{equation}

Implementation Notes:

• The scalar interpolation method is applied to the vector function in a component-wise manner.
• The function computes the interpolant for the entire grid in one call. It loops over all the grid lines along the interpolation direction and carries out the 1D interpolation along these grid lines.
• Location of cell-centers and cell interfaces along the spatial dimension of the interpolation is shown in the following figure:
  

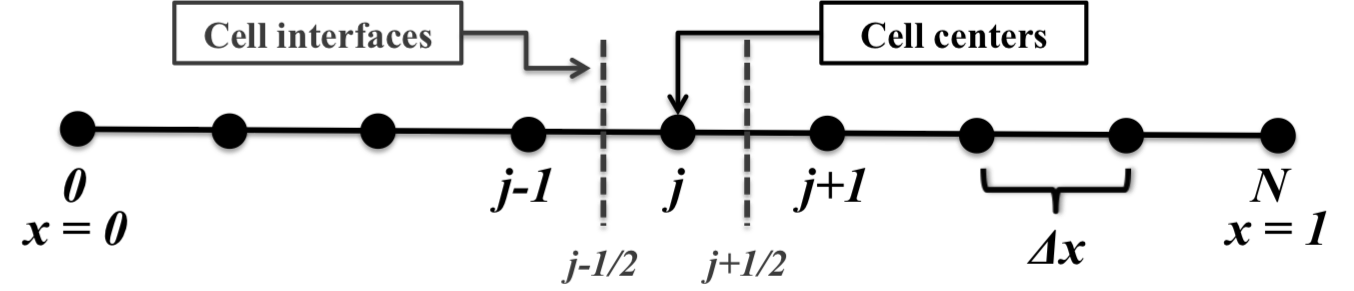
Reference:

• Liu, Y., Shu, C.-W., Zhang, M., High Order Finite Difference WENO Schemes for Nonlinear Degenerate Parabolic Equations, SIAM J. Sci. Comput., 33 (2), 2011, pp. 939-965, http://dx.doi.org/10.1137/100791002.

Function arguments:

Argument	Type	Explanation ------—
fI	double*	Array to hold the computed interpolant at the grid interfaces. This array must have the same layout as the solution, but with no ghost points. Its size should be the same as u in all dimensions, except dir (the dimension along which to interpolate) along which it should be larger by 1 (number of interfaces is 1 more than the number of interior cell centers).
fC	double*	Array with the cell-centered values of the flux function \({\bf f}\left({\bf u}\right)\). This array must have the same layout and size as the solution, with ghost points.
dir	int	Spatial dimension along which to interpolate (eg: 0 for 1D; 0 or 1 for 2D; 0,1 or 2 for 3D)
s	void*	Solver object of type HyPar: the following variables are needed - HyPar::ghosts, HyPar::ndims, HyPar::nvars, HyPar::dim_local.
m	void*	MPI object of type MPIVariables: this is needed only by compact interpolation method that need to solve a global implicit system across MPI ranks.

Parameters

fI	Array of interpolated function values at the interfaces
fC	Array of cell-centered values of the function \({\bf f}\left({\bf u}\right)\)
dir	Spatial dimension along which to interpolation
s	Object of type HyPar containing solver-related variables
m	Object of type MPIVariables containing MPI-related variables

Definition at line 56 of file Interp2PrimSecondOrder.c.

{
  HyPar         *solver = (HyPar*)        s;

  int ghosts = solver->ghosts;
  int ndims  = solver->ndims;
  int nvars  = solver->nvars;
  int *dim   = solver->dim_local;

  /* create index and bounds for the outer loop, i.e., to loop over all 1D lines along
     dimension "dir"                                                                    */
  int indexC[ndims], indexI[ndims], index_outer[ndims], bounds_outer[ndims], bounds_inter[ndims];
  _ArrayCopy1D_(dim,bounds_outer,ndims); bounds_outer[dir] =  1;
  _ArrayCopy1D_(dim,bounds_inter,ndims); bounds_inter[dir] += 1;

  int done = 0; _ArraySetValue_(index_outer,ndims,0);
  while (!done) {
    _ArrayCopy1D_(index_outer,indexC,ndims);
    _ArrayCopy1D_(index_outer,indexI,ndims);
    for (indexI[dir] = 0; indexI[dir] < dim[dir]+1; indexI[dir]++) {
      int p, qL, qR;
      _ArrayIndex1D_(ndims,bounds_inter,indexI,0,p);
      indexC[dir] = indexI[dir]-1; _ArrayIndex1D_(ndims,dim,indexC,ghosts,qL);
      indexC[dir] = indexI[dir]  ; _ArrayIndex1D_(ndims,dim,indexC,ghosts,qR);
      int v; for (v=0; v<nvars; v++) fI[p*nvars+v] = (fC[qR*nvars+v] - fC[qL*nvars+v]);
    }
    _ArrayIncrementIndex_(ndims,bounds_outer,index_outer,done);
  }
  
  return(0);
}