4th order central scheme (component-wise application to vectors) More...
#include <stdio.h>#include <stdlib.h>#include <basic.h>#include <arrayfunctions.h>#include <interpolation.h>#include <mpivars.h>#include <hypar.h>Go to the source code of this file.
Macros | |
| #define | _MINIMUM_GHOSTS_ 2 |
Functions | |
| int | Interp1PrimFourthOrderCentral (double *fI, double *fC, double *u, double *x, int upw, int dir, void *s, void *m, int uflag) |
| 4th order central reconstruction (component-wise) on a uniform grid More... | |
Detailed Description
4th order central scheme (component-wise application to vectors)
Definition in file Interp1PrimFourthOrderCentral.c.
Macro Definition Documentation
◆ _MINIMUM_GHOSTS_
| #define _MINIMUM_GHOSTS_ 2 |
Minimum number of ghost points required for this interpolation method.
Definition at line 23 of file Interp1PrimFourthOrderCentral.c.
Function Documentation
◆ Interp1PrimFourthOrderCentral()
| int Interp1PrimFourthOrderCentral | ( | double * | fI, |
| double * | fC, | ||
| double * | u, | ||
| double * | x, | ||
| int | upw, | ||
| int | dir, | ||
| void * | s, | ||
| void * | m, | ||
| int | uflag | ||
| ) |
4th order central reconstruction (component-wise) on a uniform grid
Computes the interpolated values of the first primitive of a function \({\bf f}\left({\bf u}\right)\) at the interfaces from the cell-centered values of the function using the 4th order central scheme on a uniform grid. The first primitive is defined as a function \({\bf h}\left({\bf u}\right)\) that satisfies:
\begin{equation} {\bf f}\left({\bf u}\left(x\right)\right) = \frac{1}{\Delta x} \int_{x-\Delta x/2}^{x+\Delta x/2} {\bf h}\left({\bf u}\left(\zeta\right)\right)d\zeta, \end{equation}
where \(x\) is the spatial coordinate along the dimension of the interpolation. This function computes the 4th order central numerical approximation \(\hat{\bf f}_{j+1/2} \approx {\bf h}_{j+1/2}\) as:
\begin{equation} \hat{\bf f}_{j+1/2} = -\frac{1}{12} {\bf f}_{j-1} + \frac{7}{12} {\bf f}_{j} + \frac{7}{12} {\bf f}_{j+1} - \frac{1}{12} {\bf f}_{j+2}. \end{equation}
Implementation Notes:
- The scalar interpolation method is applied to the vector function in a component-wise manner.
- Since this is a central scheme, the input argument upw has no effect.
- The function computes the interpolant for the entire grid in one call. It loops over all the grid lines along the interpolation direction and carries out the 1D interpolation along these grid lines.
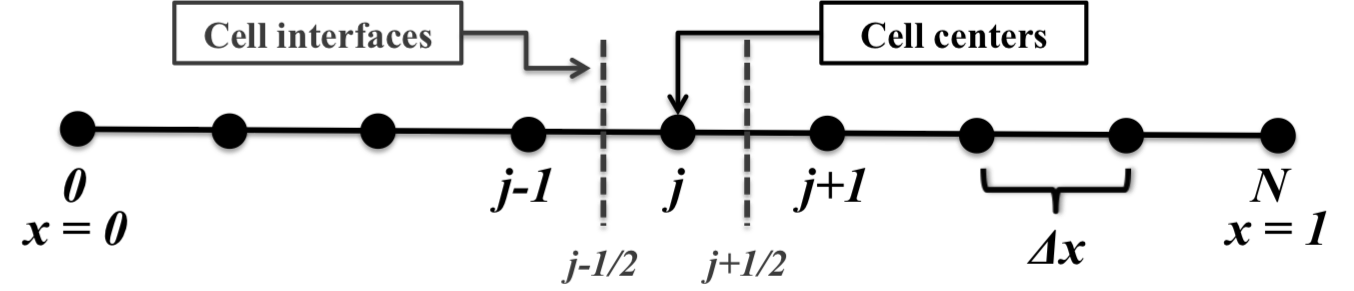
- Location of cell-centers and cell interfaces along the spatial dimension of the interpolation is shown in the following figure:
Function arguments:
| Argument | Type | Explanation ------— |
|---|---|---|
| fI | double* | Array to hold the computed interpolant at the grid interfaces. This array must have the same layout as the solution, but with no ghost points. Its size should be the same as u in all dimensions, except dir (the dimension along which to interpolate) along which it should be larger by 1 (number of interfaces is 1 more than the number of interior cell centers). |
| fC | double* | Array with the cell-centered values of the flux function \({\bf f}\left({\bf u}\right)\). This array must have the same layout and size as the solution, with ghost points. |
| u | double* | The solution array \({\bf u}\) (with ghost points). If the interpolation is characteristic based, this is needed to compute the eigendecomposition. For a multidimensional problem, the layout is as follows: u is a contiguous 1D array of size (nvars*dim[0]*dim[1]*...*dim[D-1]) corresponding to the multi-dimensional solution, with the following ordering - nvars, dim[0], dim[1], ..., dim[D-1], where nvars is the number of solution components (HyPar::nvars), dim is the local size (HyPar::dim_local), D is the number of spatial dimensions. |
| x | double* | The grid array (with ghost points). This is used only by non-uniform-grid interpolation methods. For multidimensional problems, the layout is as follows: x is a contiguous 1D array of size (dim[0]+dim[1]+...+dim[D-1]), with the spatial coordinates along dim[0] stored from 0,...,dim[0]-1, the spatial coordinates along dim[1] stored along dim[0],...,dim[0]+dim[1]-1, and so forth. |
| upw | int | Upwinding direction: if positive, a left-biased interpolant will be computed; if negative, a right-biased interpolant will be computed. If the interpolation method is central, then this has no effect. |
| dir | int | Spatial dimension along which to interpolate (eg: 0 for 1D; 0 or 1 for 2D; 0,1 or 2 for 3D) |
| s | void* | Solver object of type HyPar: the following variables are needed - HyPar::ghosts, HyPar::ndims, HyPar::nvars, HyPar::dim_local. |
| m | void* | MPI object of type MPIVariables: this is needed only by compact interpolation method that need to solve a global implicit system across MPI ranks. |
| uflag | int | A flag indicating if the function being interpolated \({\bf f}\) is the solution itself \({\bf u}\) (if 1, \({\bf f}\left({\bf u}\right) \equiv {\bf u}\)). |
- Parameters
-
fI Array of interpolated function values at the interfaces fC Array of cell-centered values of the function \({\bf f}\left({\bf u}\right)\) u Array of cell-centered values of the solution \({\bf u}\) x Grid coordinates upw Upwind direction (left or right biased) dir Spatial dimension along which to interpolation s Object of type HyPar containing solver-related variables m Object of type MPIVariables containing MPI-related variables uflag Flag to indicate if \(f(u) \equiv u\), i.e, if the solution is being reconstructed
Definition at line 62 of file Interp1PrimFourthOrderCentral.c.